프로그래머스: N으로 표현

(문제링크)

문제

아래와 같이 5와 사칙연산만으로 12를 표현할 수 있습니다.

12 = 5 + 5 + (5 / 5) + (5 / 5)
12 = 55 / 5 + 5 / 5
12 = (55 + 5) / 5

5를 사용한 횟수는 각각 6,5,4 입니다. 그리고 이중 가장 작은 경우는 4입니다.
이처럼 숫자 N과 number가 주어질 때, N과 사칙연산만 사용해서 표현 할 수 있는 방법 중 N 사용횟수의 최솟값을 return 하도록 solution 함수를 작성하세요.

제한사항

• N은 1 이상 9 이하입니다.
• number는 1 이상 32,000 이하입니다.
• 수식에는 괄호와 사칙연산만 가능하며 나누기 연산에서 나머지는 무시합니다.
• 최솟값이 8보다 크면 -1을 return 합니다.

입출력 예

N	number	return
5	12	4
2	11	3

입출력 예 설명
예제 #1
문제에 나온 예와 같습니다.

예제 #2
11 = 22 / 2와 같이 2를 3번만 사용하여 표현할 수 있습니다.

첫번째 풀이

N과 사칙연산을 사용해 number를 만들 수 있는 방법 중 N을 최소로 사용한 값을 찾아야 한다.

그래서 N을 1번 사용했을 때 number를 만들 수 있다면 1을 반환하고,
2번 사용했을 때 만들 수 있으면 2를 반환하고,
3번 사용했을 때 만들 수 있으면 3을 반환하는 걸 8까지 반복했다.

1. 반복문을 사용해서 N과 사칙연산을 i번 사용해 만들 수 있는 모든 결과값을 찾는다.
2. 그 값 중에 number가 있다면 i를 반환한다.

가능한 모든 결과 값을 저장할 때 중복값이 저장될 가능성이 높다.
그래서 Set을 사용했다.

그럼 가장 중요한 N과 사칙연산을 i번 사용해 만들 수 있는 모든 결과값을 찾는 과정은?
방법을 말하기 전에 직접 N과 사칙연산을 사용해 숫자를 만들어보자.

N의 개수	만들 수 있는 숫자들
1	N
2	NN, N+N, N-N, N*N, N/N
3	NNN, N+(N+N), N-(N+N), N*(N+N), N/(N+N), N+(N-N), N-(N-N), N*(N-N), N/(N-N), ...
...	...

너무 많다. 그만하자...

아무튼 해보면 사칙연산 결과가 중첩되는 걸 알 수 있다.

N의 개수	만들 수 있는 숫자들
1	N
2	NN + N과 N의 사칙연산
3	NNN + N과 NN의 사칙연산, N과 (N+N)의 사칙연산, N과 (N-N)의 사칙연산, N과 (N*N)의 사칙연산, N과 (N/N)의 사칙연산
4	NNNN + N을 1번 사용한 결과값과 4번 사용한 결과값의 사칙연산 + N을 2번 사용한 결과값과 2번 사용한 결과값의 사칙연산 + N을 3번 사용한 결과값과 1번 사용한 결과값의 사칙연산
...	...

반복문을 만들어 i만큼 반복되는 N을 처음에 넣어주고, (N, NN, NNN 같은 숫자)
i만큼 N을 사용하도록 사칙연산한다.

위에서 N을 1번 사용한 결과값과 4번 사용한 결과값의 사칙연산 + N을 2번 사용한 결과값과 2번 사용한 결과값의 사칙연산 ... 같은 부분을 구현하기 위해

반복문 i번째 결과값을 저장한 Set을 통째로 배열에 집어넣는다. (Set은 중복방지때문에 사용)
그럼 그 배열은 차곡차곡 Set이 쌓인다.
[N을 1번만 사용한 결과값 Set, N을 2번만 사용한 결과값 Set, N을 3번만 사용한 결과값 Set, ...]

이렇게 하면 배열에 순서대로 저장되니까 N을 i번 사용한 결과값을 쉽게 알 수 있다.

그럼 그 결과값 Set끼리의 사칙연산은 어떻게 할까?
첫번째 Set 요소와 두번째 Set 요소끼리의 모든 사칙연산을 찾는 함수를 만들었다... (이중for문😥)

Set에 다른 Set을 합쳐 하나의 Set으로 만들고 싶은데 마땅한 기본함수가 없어서 JavaScript Set 문서를 참고했다. (union은 합집합이라는 뜻)
직접 만들어도 되지만 확실히 공식문서 코드가 쓰기 편하다 😊

Set.prototype.union = function(setB) {
    var union = new Set(this);
    for (var elem of setB) {
        union.add(elem);
    }
    return union;
}

소스코드

// Set1과 Set2의 사칙연산 결과 Set 반환
function operation(op1, op2) {
    let set = new Set();
    for (let item1 of op1) {
        for (let item2 of op2) {
            set.add(item1 + item2);
            set.add(item1 - item2);
            set.add(item1 * item2);
            set.add(Math.floor(item1 / item2));
        }
    }
    return set;
}

// N을 count만큼 반복한 숫자 반환
function Nrepeat(N, count) {
    let num = '';
    for (let i=0; i<count; i++) num += N;
    return Number(num);
}

//  Set + Set (합집합 함수)
Set.prototype.union = function(setB) {
    var union = new Set(this);
    for (var elem of setB) {
        union.add(elem);
    }
    return union;
}

function solution(N, number) { 
    // 모든 경우의 수 계산
    let calcul = [];
    for (let i=1; i<=8; i++) {
        let set = new Set();
        set.add(Nrepeat(N, i));
        
        for (let j=1; j<i; j++) {
            set = set.union(operation(calcul[j-1], calcul[i-j-1]));
        }
        // number가 있다면 N을 사용한 횟수 반환
        if (set.has(number)) return i;
        else calcul.push(set);
    }
    // 최솟값이 8보다 클 때
    return -1;
}

실행 결과

두번째 풀이

Set 말고 Array를 사용해봤다.
값이 너무 불어나는 것을 방지하기 위해 Set으로 중복제거하는 부분 빼고 기본적인 연산은 Array로 했다.
Array.includes()로 검사해 중복이 아닐때만 push하는 방법은 실행시간을 너무 많이 잡아먹었기 때문에 Set으로 변환해서 중복을 제거해줘야 했다.

이렇게 해본 이유는 Set보다 Array의 기본연산이 더 빠르다는 글을 보고 시간효율이 더 좋아질지 궁금했기 때문이다.

소스코드

function operation(op1, op2) {
    let arr = [];
    for (let i=0; i<op1.length; i++) {
        for (let j=0; j<op2.length; j++) {
            arr.push(op1[i]+op2[j], op1[i]-op2[j], op1[i]*op2[j], Math.floor(op1[i]/op2[j]));
        }
    }
    return arr;
}

function Nrepeat(N, count) {
    let num = 0;
    for (let i=0; i<count; i++) num += N * Math.pow(10, i); 
    return num;
}

function solution(N, number) {
    // 모든 경우의 수 계산
    let calcul = [];
    for (let i=1; i<=8; i++) {
        let arr = [];
        arr.push(Nrepeat(N, i));
        for (let j=1; j<i; j++) {
            arr.push(...operation(calcul[j-1], calcul[i-j-1]));
        }
        // 중복 제거
        arr = [...new Set(arr)];
        if (arr.includes(number)) return i;
        else calcul.push(arr);
        
    }
    return -1;
}

실행 결과

첫번째 풀이로 했을 때 실행시간이 오래 걸리던 테스트들이 두번째 풀이로 했을 때 더 길어졌다.
원래 실행시간이 짧던 테스트들은 더 짧아진 경우도 있는 걸 보면 대용량일수록 Set이 더 유리한 것 같다.

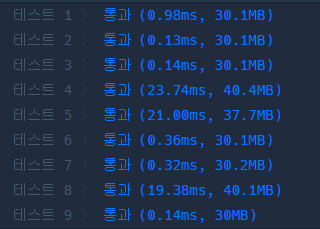
느낀점

Set을 사용한 예제와 Array를 사용한 예제를 각각 3번 실행해본 결과, 대체적으로 위 사진과 비슷하게 나왔다.
Array보다 Set의 실행 시간이 더 짧은 이유는 무엇일까?

Set은 중복된 값을 저장할 수 없는 자료구조이다.
값을 넣을 때 중복 유무를 체크한 후 넣어주기 때문에 Set의 기본적인 연산속도는 Array보다 느리다.

실제로 데이터가 적은 테스트의 경우 Array 사용방법이 더 빨랐지만, 데이터 양이 더 많아질수록 Set 사용방법이 더 빨랐다.
데이터 양이 많을수록 arr = [...new Set(arr)]; 에서 많은 시간을 잡아먹기 때문일 것이라고 추측된다.

Array의 기본연산속도가 더 빠르더라도 중복방지를 위해 다시 Set으로 변환하는 과정을 거치는 것보다 처음부터 Set을 사용해 중복방지하는 것이 맞는 것 같다.