강의자 : 투빅스 16기 이승주

Contents
Unit 01 ㅣ Introduction
Unit 02 ㅣ Methodology
Unit 03 ㅣ Experiments
Unit 04 ㅣ Conclusion and Future Work

1. Introduction

1. Introduction - Motivation

• Two key components in learnable CF models
  • Embedding: which transforms users and items to vectorized representations
  • Interaction modeling: which reconstructs historical interactions based on the embeddings.
    • For example, matrix factorization (MF) directly embeds user/item ID as vector and models user-item interaction with inner product
• Neural collaborative filtering models replace the MF interaction function of inner product with nonlinear neural networks, and translation-based CF models instead use Euclidean distance metric as the interaction function, among others.

1. Introduction – Problem Statement

• Not satisfactory embeddings for CF
  • The key reason is that the embedding function lacks an explicit encoding of the crucial collaborative signal, which is latent in user-item interactions to reveal the behavioral similarity between users (or items). Most existing methods build the embedding function with the descriptive features only, without considering the user-item interactions — which are only used to define the objective function for model training .
  • While intuitively useful to integrate user-item interactions into the embedding function, it is non-trivial to do it well. In particular, the scale of interactions can easily reach millions or even larger in real applications, making it difficult to distill the desired collaborative signal.

1. Introduction - Contribution

In this work, we tackle the challenge by exploiting the high-order connectivity from user item interactions, a natural way that encodes collaborative signal in the interaction graph structure.

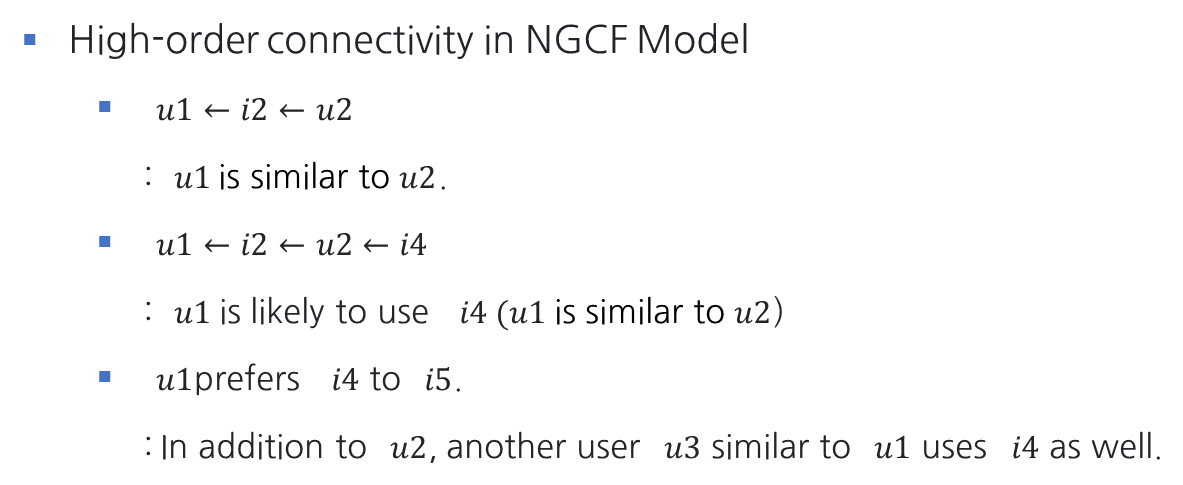
1. Introduction - Contribution

• We highlight the critical importance of explicitly exploiting the collaborative signal in the embedding function of model-based CF methods.
• We propose NGCF, a new recommendation framework based on graph neural network, which explicitly encodes the collaborative signal in the form of high-order connectivities by performing embedding propagation.
• We conduct empirical studies on three million-size datasets. Extensive results demonstrate the state-of-the-art performance of NGCF and its effectiveness in improving the embedding quality with neural embedding propagation.

2. Methodology

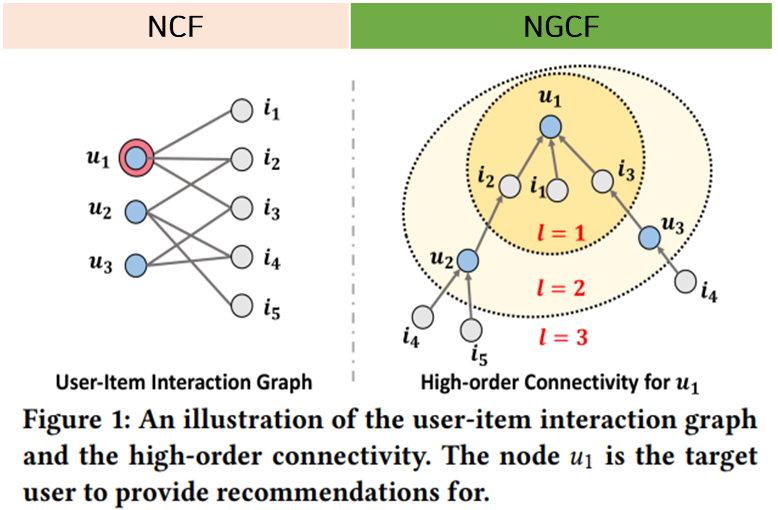
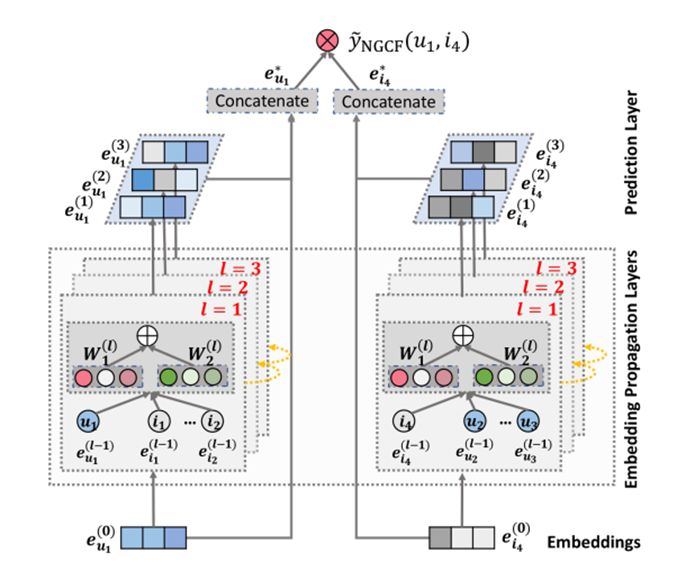
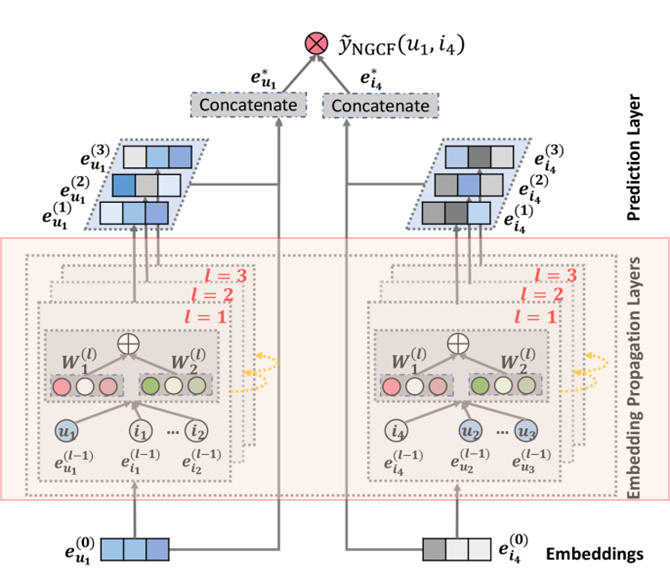
The architecture of Neural Graph Collaborative Filtering Model

• Embedding Layer
• Multiple embedding propagation Layers
• Prediction Layer
• Concatenation Layer
  

2.1 Embedding Layer

• User 𝑢 and item 𝑖 with an embedding vector 𝑒𝑢 ∈ 𝑅𝑑 (𝑒𝑖 ∈ 𝑅𝑑), where 𝑑 denotes the embedding size.
  
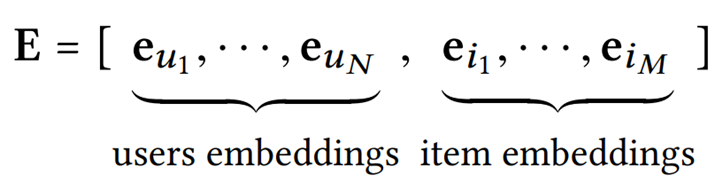
• In traditional recommender models like MF and neural collaborative filtering, these ID embeddings are directly fed into an interaction layer (or operator) to achieve the prediction score.
• In contrast, in our NGCF framework, we refine the embeddings by propagating them on the user-item interaction graph. This leads to more effective embeddings for recommendation, since the embedding refinement step explicitly injects collaborative signal into embeddings.

2.2 Embedding Propagation Layers

The message-passing architecture of GNNs in order to capture CF signal along the graph structure and refine the embeddings of users and items.

2.2 Embedding Propagation Layers

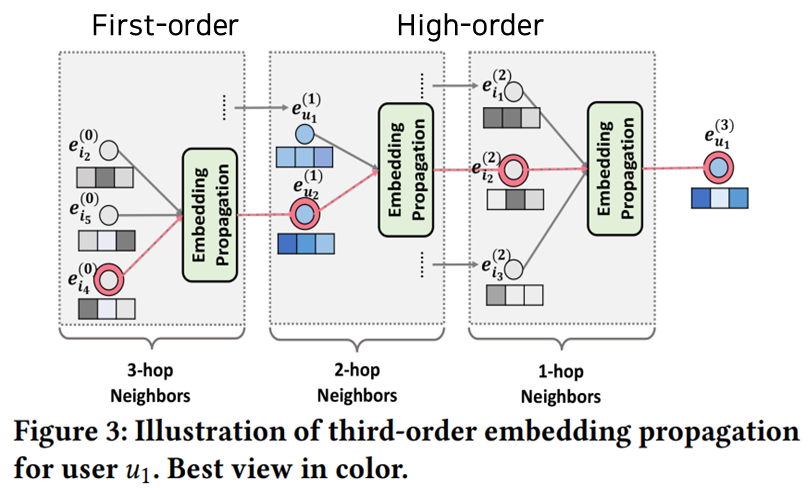
In this paper, first-order propagation → high-order propagation is being explained.

• First-order propagation : Radio waves from the first Embedded Propagation Layer
• High-order propagation : Radio waves from the second to 𝑙−th Embedded Propagation Layer
  

2.2.1 First-order Propagation

• Intuitively, the interacted items provide direct evidence on a user’s preference; analogously, the users that consume an item can be treated as the item’s features and used to measure the collaborative similarity of two items.
• We build upon this basis to perform embedding propagation between the connected users and items, formulating the process with two major operations: message construction and message aggregation.

2.2.1 First-order Propagation

• Two major operations : Message construction / Message aggregation.

• Message construction
  

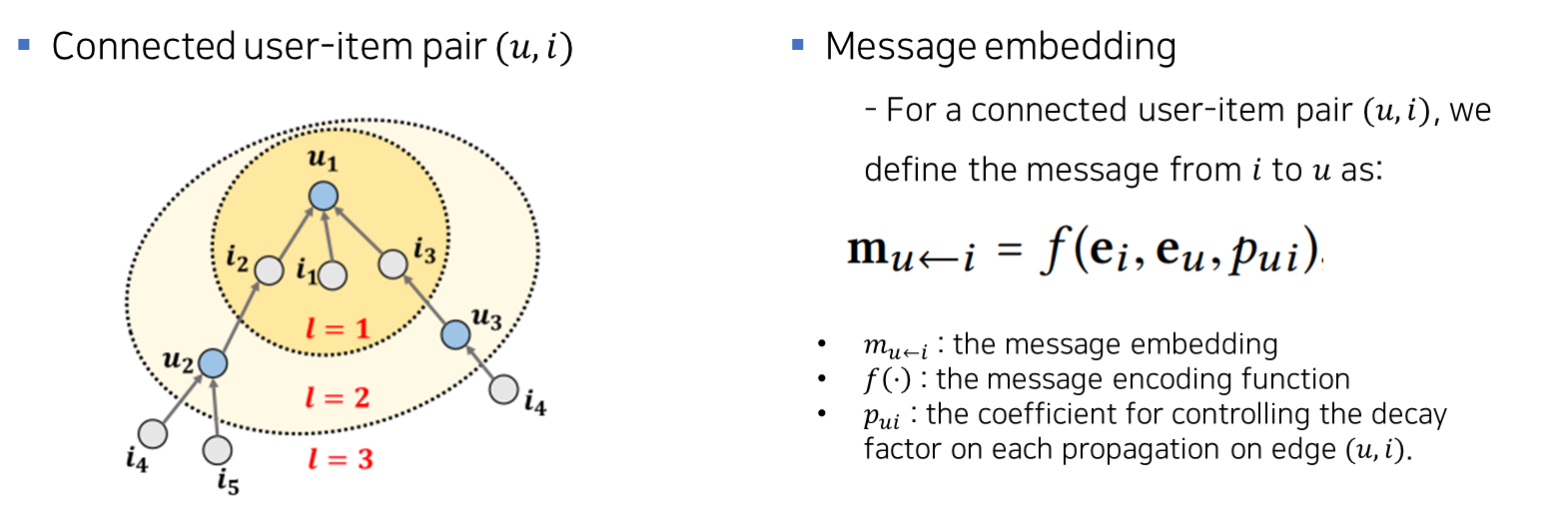
2.2.1 First-order Propagation

• Message Construction
  This makes the message dependent on the affinity between $𝑒_𝑖$ and $𝑒_𝑢$, passing more messages from the similar items.
  Following the graph convolutional network , we set $𝑝_{𝑢𝑖}$ as the graph Laplacian norm $1/√(|𝑁_𝑢||𝑁_𝑖|)$ where $𝑁_𝑢$ and $𝑁_𝑖$ denote the first-hop neighbors of user 𝑢 and item 𝑖.

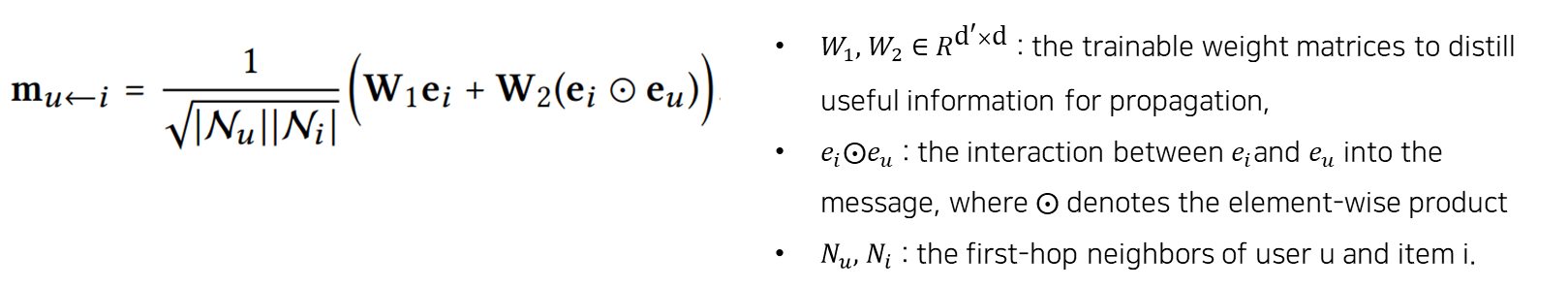
2.2.1 First-order Propagation

• Message Aggregation
  In this stage, we aggregate the messages propagated from user’s neighborhood to refine user’s representation. Specifically, we define the aggregation function as:
  

2.2.2 High-order Propagation

• High-order Propagation
  • With the representations augmented by first-order connectivity modeling, we can stack more embedding propagation layers to explore the high-order connectivity information.
  • Such high-order connectivities are crucial to encode the collaborative signal to estimate the relevance score between a user and item. By stacking 𝑙 embedding propagation layers, a user (and an item) is capable of receiving the messages propagated from its 𝑙-hop neighbors.
  • $𝑒_𝑢^𝑙$ : the representation of user 𝑢 In the 𝑙-th step

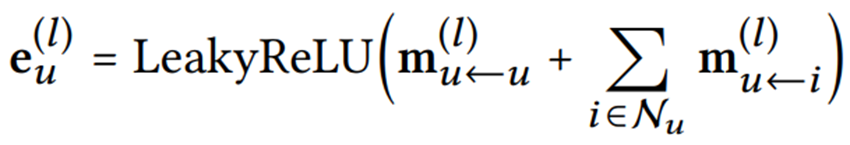
2.2.2 High-order Propagation

• High-order Propagation
  $𝑒_𝑢^𝑙$ : the representation of user 𝑢 In the 𝑙-th step

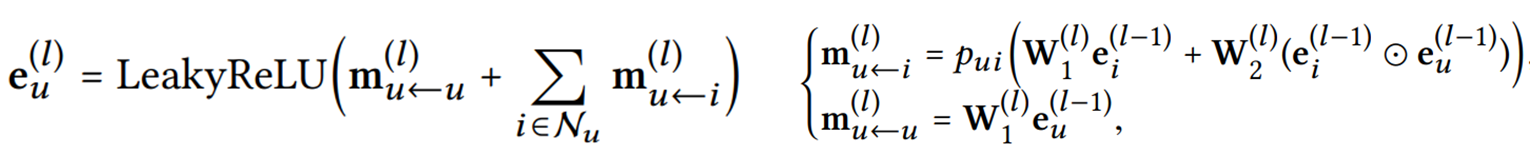
• where $𝑊_1^𝑙$, $𝑊_2^𝑙$ $∈ ℝ^{𝑑_𝑙×𝑑_{𝑙−1}}$are the trainable transformation matrices, $𝑑_𝑙$ is the transformation size.
• 𝑝𝑢𝑖 is the graph Laplacian norm $1/√|𝑁𝑢||𝑁_𝑖| $ , the coefficient for controling the decay factor on each propagation on edge (𝑢,𝑖).
• $𝑒_𝑖^{(𝑙−1)}$ is the item representation generated from the previous message-passing steps, memorizing the messages from its $(𝑙−1)$−hop neighbors. It further contributes to the representation of user 𝑢 at layer 𝑙.
• Analogously, we can obtain the representation for item 𝑖 at the layer 𝑙.

2.2.2 High-order Propagation

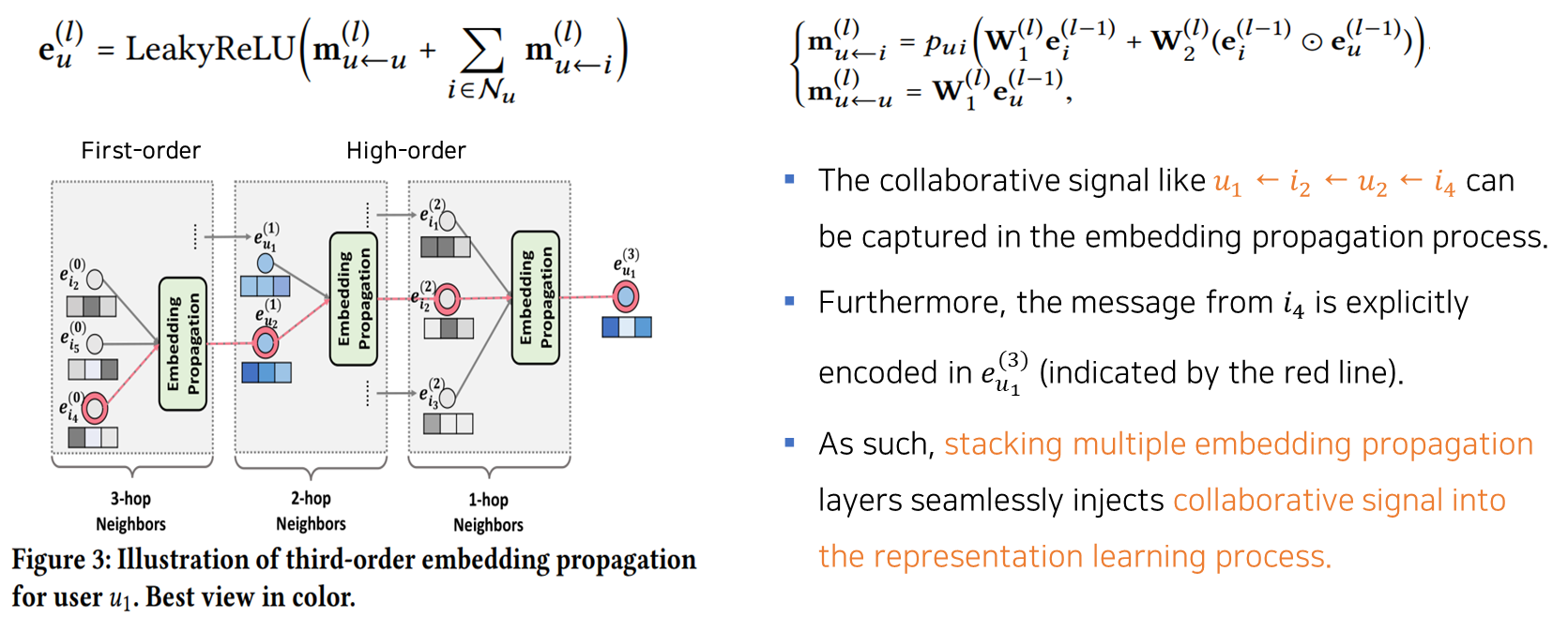
2.3 Model Prediction

After propagating with L layers, we obtain multiple representations for user 𝑢 and item 𝑖, namely

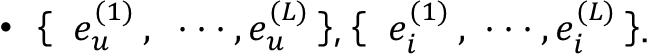
• Since the representations obtained in different layers emphasize the messages passed over different connections, they have different contributions in reflecting user preference.
• As such, we concatenate them to constitute the final embedding for a user; Using concatenation has been shown quite effectively in a recent work of graph neural networks, which refers to layer-aggregation mechanism.
  
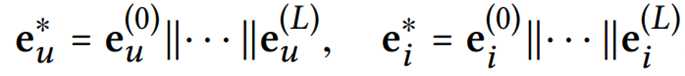
• Finally, we conduct the inner product to estimate the user’s preference towards the target item:
  

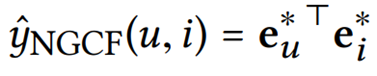
2.4 Optimization

• To learn model parameters, we optimize the pairwise BPR loss considering the relative order between observed and unobserved user-item interactions.
• We adopt mini-batch Adam to optimize the prediction model and update the model parameters. The objective function is as follows,
  

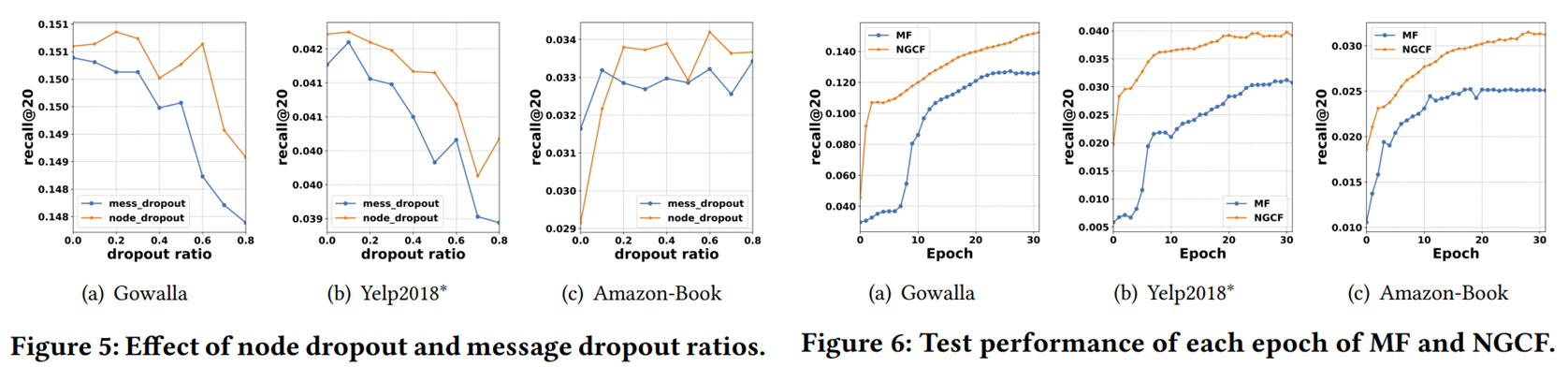
2.4.2 Message and Node Dropout

To prevent neural networks from overfitting, we propose to adopt two dropout techniques in NGCF :

• Message dropout
  • randomly drops out the messages being propagated in High-order connectivity. As such, in the 𝑙-th propagation layer, only partial messages contribute to the refined representations.
  • It endows the representations more robustness against the presence or absence of single connections between users and items.
• Node dropout
  • randomly block a particular node and discard all its outgoing messages. For the l-th propagation layer, we randomly drop $(𝑀 + 𝑁)𝑝_2$ nodes of the Laplacian matrix, where $𝑝_2$ is the dropout ratio.
  • It focuses on reducing the influences of particular users or items.

3. Experiments

We perform experiments on three real-world datasets to evaluate our proposed method, especially the embedding propagation layer. We aim to answer the following research questions:

• RQ1: How does NGCF perform as compared with state-of-the-art CF methods?
• RQ2: How do different hyper-parameter settings (e.g., depth of layer, embedding propagation layer, layer-aggregation mechanism, message dropout, and node dropout) affect NGCF?
• RQ3: How do the representations benefit from the high-order connectivity?

3. Experiments Settings

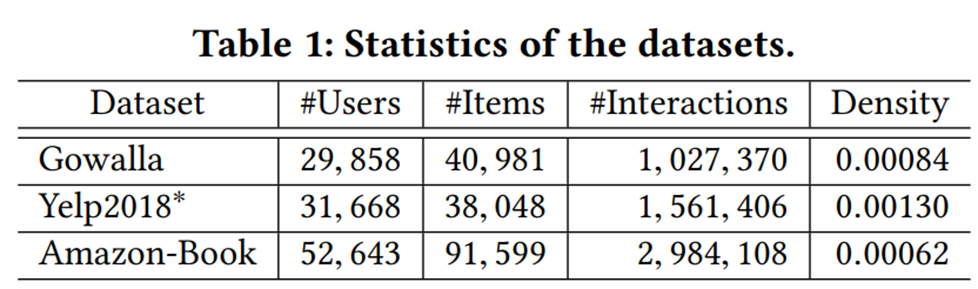
• Datasets
  
• Evaluation Metrics
  • To evaluate the effectiveness of top-K recommendation and preference ranking
  • Recall@K
  • NDCG@K (By default, we set K = 20.)

3. Experiments

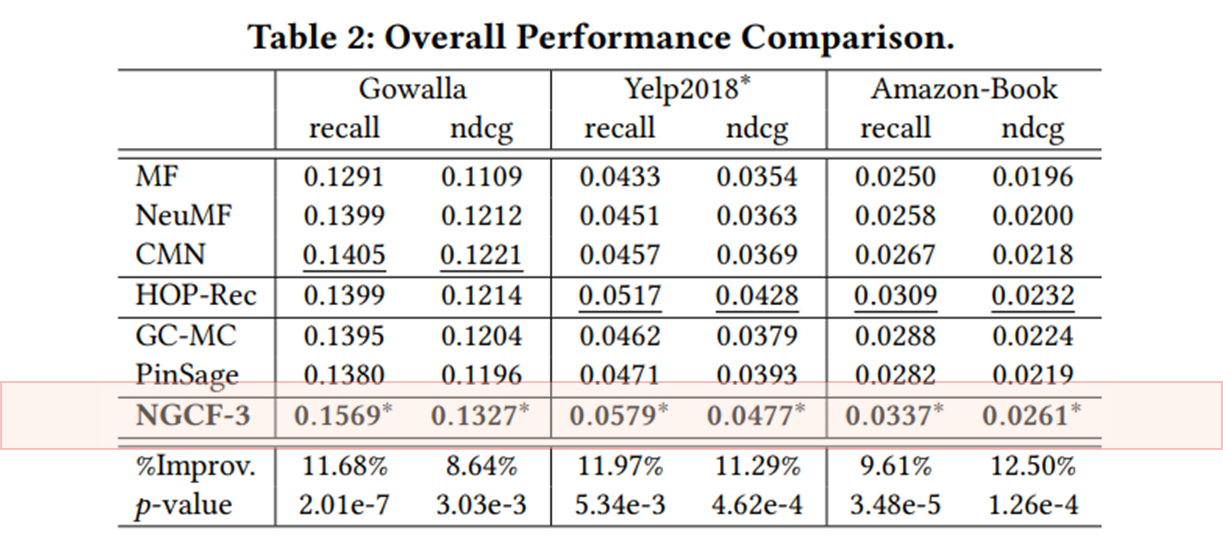
• RQ1: How does NGCF perform as compared with state-of-the-art CF methods?

• RQ2: How do different hyper-parameter settings (e.g., depth of layer, embedding propagation layer, layer-aggregation mechanism, message dropout, and node dropout) affect NGCF?

• RQ3: How do the representations benefit from the high-order connectivity?
  

4. Conclusion

• In this work, we explicitly incorporated collaborative signal into the embedding function of model-based CF devising a new framework NGCF, which achieves the target by leveraging high-order connectivities in the user-item integration graph.
• The key of NGCF is the newly proposed embedding propagation layer, based on which we allow the embeddings of users and items interact with each other to harvest the collaborative signal.
• Extensive experiments on three real-world datasets demonstrate the rationality and effectiveness of injecting the user-item graph structure into the embedding learning process.

4. Future Work

• We will further improve NGCF by incorporating the attention mechanism to learn variable weights for neighbors during embedding propagation and for the connectivities of different orders. This will be beneficial to model generalization and interpretability.
• Moreover, we are interested in exploring the adversarial learning on user/item embedding and the graph structure for enhancing the robustness of NGCF.