아래 모든 문제들은 프로그래머스에서 제공 되는 문제를 이용하였습니다, 감사합니다.
- 4번 수식최대화 못품
1. 최댓값과 최솟값
문제 설명
문자열 s에는 공백으로 구분된 숫자들이 저장되어 있습니다. str에 나타나는 숫자 중 최소값과 최대값을 찾아 이를 "(최소값) (최대값)"형태의 문자열을 반환하는 함수, solution을 완성하세요.
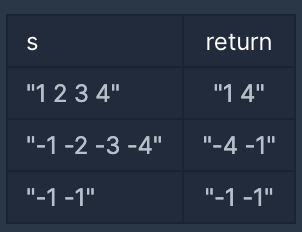
예를들어 s가 "1 2 3 4"라면 "1 4"를 리턴하고, "-1 -2 -3 -4"라면 "-4 -1"을 리턴하면 됩니다.
제한 조건
- s에는 둘 이상의 정수가 공백으로 구분되어 있습니다.
입출력 예
풀이
#include <vector>
#include <set>
#include <iostream>
#include <algorithm>
using namespace std;
string solution(string s) {
//set <int> tmp;
vector<int> tmp;
string answer = "";
int flag = 0;
int j = 0;
for(int i = 0; i < s.size(); i++)
{
if(s[i] == '-')
flag = 1;
if(isdigit(s[i]))
{
answer = "";
if (flag == 1)
{
flag--;
answer += '-';
}
for(j = 0; isdigit(s[i + j]); j++)
{
answer += s[i + j];
}
if (answer != "")
{
tmp.push_back(stoi(answer));}
//tmp.insert(stoi(answer));
// set 으로 어떻게 맨앞 맨뒤 접근하는지 알아보기.
}
if (j > 0)
i = i + j - 1;
}
sort(tmp.begin(), tmp.end(), [](int &a, int &b){return a > b;});
answer = "";
answer += to_string(tmp[tmp.size() - 1]);
answer += " ";
answer += to_string(tmp[0]);
return answer;
}설명
- 입력값이 문자열로 주어져서, 숫자만 분리해서 벡터 배열로 넣어주었다.
- 그리고 sort로 정렬시켜주고 첫 값과 끝값만 리턴시켜주엇는데, 정렬할때 리턴 시켜주거나, 문자열에서 벡터로 넣을떄 한번에 리턴 시켜주는 방법도 있을거 같다.
2. 최솟값 만들기
문제 설명
길이가 같은 배열 A, B 두개가 있습니다. 각 배열은 자연수로 이루어져 있습니다.
배열 A, B에서 각각 한 개의 숫자를 뽑아 두 수를 곱합니다. 이러한 과정을 배열의 길이만큼 반복하며, 두 수를 곱한 값을 누적하여 더합니다. 이때 최종적으로 누적된 값이 최소가 되도록 만드는 것이 목표입니다. (단, 각 배열에서 k번째 숫자를 뽑았다면 다음에 k번째 숫자는 다시 뽑을 수 없습니다.)
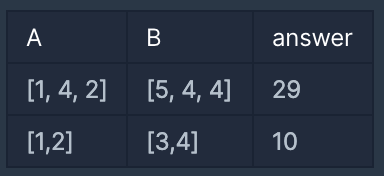
예를 들어 A = [1, 4, 2] , B = [5, 4, 4] 라면
- A에서 첫번째 숫자인 1, B에서 두번째 숫자인 5를 뽑아 곱하여 더합니다. (누적된 값 : 0 + 5(1x5) = 5)
- A에서 두번째 숫자인 4, B에서 세번째 숫자인 4를 뽑아 곱하여 더합니다. (누적된 값 : 5 + 16(4x4) = 21)
- A에서 세번째 숫자인 2, B에서 첫번째 숫자인 4를 뽑아 곱하여 더합니다. (누적된 값 : 21 + 8(2x4) = 29)
즉, 이 경우가 최소가 되므로 29를 return 합니다.
배열 A, B가 주어질 때 최종적으로 누적된 최솟값을 return 하는 solution 함수를 완성해 주세요.
제한사항
- 배열 A, B의 크기 : 1,000 이하의 자연수
- 배열 A, B의 원소의 크기 : 1,000 이하의 자연수
입출력 예
풀이
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int solution(vector<int> A, vector<int> B)
{
int answer = 0;
sort(A.begin(), A.end());
sort(B.begin(), B.end(), [](int a, int b){
return a > b;
});
for (int i = 0; i < A.size(); i++)
answer += A[i] * B[i];
return answer;
}설명
- 두 배열들을 모두 소트시켜주고, 원하는 인덱스들을 뽑아서, 더해주었다.
3. 피보나치 수
문제 설명
피보나치 수는 F(0) = 0, F(1) = 1일 때, 1 이상의 n에 대하여 F(n) = F(n-1) + F(n-2) 가 적용되는 수 입니다.
예를들어
F(2) = F(0) + F(1) = 0 + 1 = 1
F(3) = F(1) + F(2) = 1 + 1 = 2
F(4) = F(2) + F(3) = 1 + 2 = 3
F(5) = F(3) + F(4) = 2 + 3 = 5
와 같이 이어집니다.
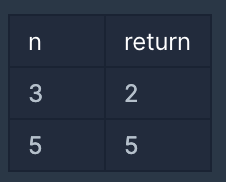
2 이상의 n이 입력되었을 때, n번째 피보나치 수를 1234567으로 나눈 나머지를 리턴하는 함수, solution을 완성해 주세요.
제한 사항
- n은 1이상, 100000이하인 자연수입니다.
입출력 예
풀이
#include <string>
#include <vector>
using namespace std;
int solution(int n) {
vector<int> number_save;
number_save.push_back(0);
number_save.push_back(1);
for (int i = 2; i <= n; i++)
{
number_save.push_back(number_save[i-2] + number_save[i-1]);
}
return number_save[n];
}설명
- 이문제의 가장 큰 문제점은, 효율성 인거 같다.
- 그냥 단순하게 for 문으로 더해서 구하면, 속도가 오래 걸려서, 사용했던 값들을 배열 단위로 넣어서 저장해 주었다.
4. [카카오 인턴] 수식 최대화 (못 풀었다.) (못 풀었다.)
문제 설명
IT 벤처 회사를 운영하고 있는 라이언은 매년 사내 해커톤 대회를 개최하여 우승자에게 상금을 지급하고 있습니다.
이번 대회에서는 우승자에게 지급되는 상금을 이전 대회와는 다르게 다음과 같은 방식으로 결정하려고 합니다.
해커톤 대회에 참가하는 모든 참가자들에게는 숫자들과 3가지의 연산문자(+, -, ) 만으로 이루어진 연산 수식이 전달되며, 참가자의 미션은 전달받은 수식에 포함된 연산자의 우선순위를 자유롭게 재정의하여 만들 수 있는 가장 큰 숫자를 제출하는 것입니다.
단, 연산자의 우선순위를 새로 정의할 때, 같은 순위의 연산자는 없어야 합니다. 즉, + > - > 또는 - > > + 등과 같이 연산자 우선순위를 정의할 수 있으나 +, > - 또는 * > +,-처럼 2개 이상의 연산자가 동일한 순위를 가지도록 연산자 우선순위를 정의할 수는 없습니다. 수식에 포함된 연산자가 2개라면 정의할 수 있는 연산자 우선순위 조합은 2! = 2가지이며, 연산자가 3개라면 3! = 6가지 조합이 가능합니다.
만약 계산된 결과가 음수라면 해당 숫자의 절댓값으로 변환하여 제출하며 제출한 숫자가 가장 큰 참가자를 우승자로 선정하며, 우승자가 제출한 숫자를 우승상금으로 지급하게 됩니다.
예를 들어, 참가자 중 네오가 아래와 같은 수식을 전달받았다고 가정합니다.
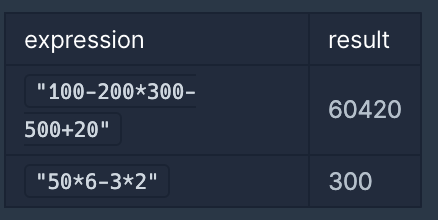
"100-200*300-500+20"
일반적으로 수학 및 전산학에서 약속된 연산자 우선순위에 따르면 더하기와 빼기는 서로 동등하며 곱하기는 더하기, 빼기에 비해 우선순위가 높아 > +,- 로 우선순위가 정의되어 있습니다.
대회 규칙에 따라 + > - > 또는 - > > + 등과 같이 연산자 우선순위를 정의할 수 있으나 +, > - 또는 > +,- 처럼 2개 이상의 연산자가 동일한 순위를 가지도록 연산자 우선순위를 정의할 수는 없습니다.
수식에 연산자가 3개 주어졌으므로 가능한 연산자 우선순위 조합은 3! = 6가지이며, 그 중 + > - > 로 연산자 우선순위를 정한다면 결괏값은 22,000원이 됩니다.
반면에 * > + > - 로 연산자 우선순위를 정한다면 수식의 결괏값은 -60,420 이지만, 규칙에 따라 우승 시 상금은 절댓값인 60,420원이 됩니다.
참가자에게 주어진 연산 수식이 담긴 문자열 expression이 매개변수로 주어질 때, 우승 시 받을 수 있는 가장 큰 상금 금액을 return 하도록 solution 함수를 완성해주세요.
[제한사항]
expression은 길이가 3 이상 100 이하인 문자열입니다.
expression은 공백문자, 괄호문자 없이 오로지 숫자와 3가지의 연산자(+, -, ) 만으로 이루어진 올바른 중위표기법(연산의 두 대상 사이에 연산기호를 사용하는 방식)으로 표현된 연산식입니다. 잘못된 연산식은 입력으로 주어지지 않습니다.
즉, "402+-561"처럼 잘못된 수식은 올바른 중위표기법이 아니므로 주어지지 않습니다.
expression의 피연산자(operand)는 0 이상 999 이하의 숫자입니다.
즉, "100-2145*458+12"처럼 999를 초과하는 피연산자가 포함된 수식은 입력으로 주어지지 않습니다.
"-56+100"처럼 피연산자가 음수인 수식도 입력으로 주어지지 않습니다.
expression은 적어도 1개 이상의 연산자를 포함하고 있습니다.
연산자 우선순위를 어떻게 적용하더라도, expression의 중간 계산값과 최종 결괏값은 절댓값이 263 - 1 이하가 되도록 입력이 주어집니다.
같은 연산자끼리는 앞에 있는 것의 우선순위가 더 높습니다.
입출력 예
풀이
#include <string>
#include <vector>
#include <iostream>
#include <map>
using namespace std;
void calculation(map<char, int> si, string expression, long long &answer)
{
vector<int> st;
vector<char> si_arr;
int a = {0 , 0};
string tmp;
int j = 0;
int save;
//cout << si['*'] << " " << si['+'] << " " << si['-'] << endl;
for(int i = 0; i < expression.size(); i++)
{
if (isdigit(expression[i]) != 0)
{
tmp = "";
for (j = 0; isdigit(expression[j + i]) != 0; j++)
{
tmp += expression[j + i];
}
i += j - 1;
st.push_back(stol(tmp));
}
else{
if(si_arr.size() == 0)
si_arr.push_back(expression[i]);
else
{
if(si[si_arr[si_arr.size - 1]] < si[expression[i]])
{
si_arr.push_back(expression[i]);
}
else
{
if(si_arr[si_arr.size() - 1] == '*')
{
save = st[st.size() - 2] * st[st.size() - 1];
}
else if(si_arr[si_arr.size() - 1] == '+')
{
save = st[st.size() - 2] + st[st.size() - 1];
}
else if(si_arr[si_arr.size() - 1] == '-')
{
save = st[st.size() - 2] - st[st.size() - 1];
}
st
}
}
}
}
// for(int i = 0; i < st.size(); i++)
// {
// cout << st[i] << " ";
// }
// cout << "==\n";
// for(int i = 0; i < si_arr.size(); i++)
// {
// cout << si_arr[i];
// }
//cout << si[0] << " " << si[1] << " " << si[2] << endl;
return ;
}
long long solution(string expression) {
long long answer = 0;
vector<char> sign = {'*', '+', '-'};
// vector<char> si(3, 0);
map <char, int> si;
//cout << si[0];
for (int i = 0; i < sign.size(); i++)
{
for (int j = 0; j < sign.size(); j++)
{
if (sign[j] == sign[i])
continue;
for (int z = 0; z < sign.size(); z++)
{
if(sign[j] == sign[z] || sign [z] == sign[i])
continue;
// si[0] = sign[i]; si[1] = sign[j]; si[2] = sign[z];
//cout << si[0] << " " << si[1] << " " << si[2] << endl;
//cout << sign[i] << " " << sign[j] << " " << sign[z] << endl;
si[sign[i]] = 3; si[sign[j]] = 2; si[sign[z]] = 1;
calculation(si, expression, answer);
}
}
}
return answer;
}설명
- 이 문제를 못풀었다. 다른 분들 풀이 법을 보니까, 우선순위인 기호들 부터 나열하고, 기열들을 베이스로, 먼저오는 기호들을 계산하고,문자열 사이에 다시 넣어주는 방법으로 계산을 햇다.
- 스터디 동료분은, 후위표기법을 사용해서 문제를 해결하셨는데, 이 방법은 너무 어려워서 접근하지 못했다 ㅠ.ㅠ.
- 다시 천천히 풀어보자.
5. 행렬의 곱셈
문제 설명
2차원 행렬 arr1과 arr2를 입력받아, arr1에 arr2를 곱한 결과를 반환하는 함수, solution을 완성해주세요.
제한 조건
- 행렬 arr1, arr2의 행과 열의 길이는 2 이상 100 이하입니다.
- 행렬 arr1, arr2의 원소는 -10 이상 20 이하인 자연수입니다.
- 곱할 수 있는 배열만 주어집니다.
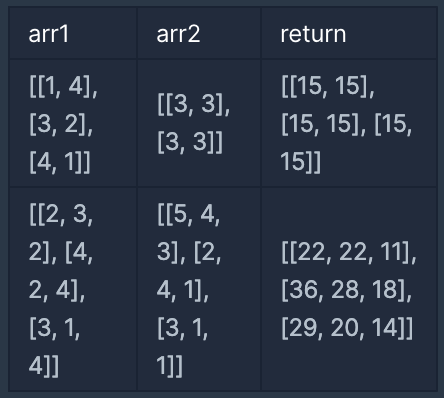
입출력 예
풀이
#include <string>
#include <vector>
using namespace std;
vector<vector<int>> solution(vector<vector<int>> arr1, vector<vector<int>> arr2) {
vector<vector<int>> answer;
vector<int> tmp;
int z = 0;
int save = 0;
for(int i = 0; i < arr1.size(); i++)
{
tmp.clear();
for(int z = 0; z < arr2[0].size(); z++)
{
save = 0;
for(int j = 0; j < arr1[0].size(); j++)
{
save += arr2[j][z] * arr1[i][j];
}
tmp.push_back(save);
}
answer.push_back(tmp);
}
return answer;
}설명
- 행렬 곱을 생각하며, 풀면 해결되는 문제엿다.
- 그런데 인덱스가 너무 보잡해서 생각보다 많이 햇갈렸다.
- 종이에 써가며 푸는게 이해도 잘되고 쉽게 푸는 방법인거 같다.