파트 1 - 4) 자료구조와 자료형 - 2) 숫자형

Lee·2021년 10월 24일

모던 자바스크립트 튜토리얼 정복하기

목록 보기

31/43

숫자형에는 number와 BigInt가 있다. (BigInt는 잘 쓰이지 않아 별도의 챕터에서 다룬다)

숫자를 입력하는 다양한 방법

0을 많이 사용하면 헷갈리기 때문에 e를 사용한다.
자바스크립트에서는 숫자 옆에 'e'를 붙이고 0의 개수를 그 옆에 쓰면 숫자 길이를 줄일 수 있다. ex) 1e9 == 1000000000

즉, 'e'는 e 왼쪽 수에 e 오른쪽에 있는 수만큼 10의 거듭제곱을 곱하는 효과가 있다.
ex)

<script>
  1e3 = 1 * 1000
  1.23e6 = 1.23 * 1000000
</script>

소수점 단위의 아주 작은 숫자를 표현할 때도 'e'를 사용할 수 있다.
let ms = 1e-6; // 0.000001, 1에서 왼쪽으로 6번 소수점 이동
이렇게 'e' 우측에 음수가 있으면, 이 음수의 절댓값 만큼 10을 거듭제곱한 수로 나누는 것을 의미한다.

16진수, 2진수, 8진수

16진수는 0x를 사용해 표현할 수 있다. (파이썬을 처음 배울때 봤던 기억이 있다)

<script>
  alert( 0xff ); // 255
  alert( 0xFF ); // 255 (대·소문자를 가리지 않으므로 둘 다 같은 값을 나타낸다)
</script>

2진수와 8진수는 각각 접두사 0b, 0o를 사용해 간단히 나타낼 수 있다.

<script>
  let a = 0b11111111; // 255의 2진수
  let b = 0o377; // 255의 8진수

  alert( a == b ); // true, 진법은 다르지만, a와 b는 같은 수임
</script>

이 세개 진법을 제외한 진법을 사용하려면 함수 parseInt를 사용해야한다.

toString(base)

num.toString(base) 메서드는 base진법으로 num을 표현한 후, 이를 문자형으로 변환해 반환한다. base 진법이라는 건 처음 본다.

<script>
  let num = 255;

  alert( num.toString(16) );  // ff
  alert( num.toString(2) );   // 11111111
</script>

base는 몇진법을 쓸 건지 넣어주는 값인데 2~36까지 쓸 수 있고 기본값은 10이다.

각각의 base 사용례는 아래와 같다.

base=16 – 16진수 색, 문자 인코딩 등을 표현할 때 사용. 숫자는 0부터 9, 10 이상의 수는 A부터 F를 사용하여 나타낸다.

base=2 – 비트 연산 디버깅에 주로 쓰인다. 숫자는 0 또는 1이 될 수 있다.

base=36 – 사용할 수 있는 base 중 최댓값으로, 0..9와 A..Z를 사용해 숫자를 표현.
알파벳 전체가 숫자를 나타내는 데 사용되고 36 베이스는 url을 줄이는 것과 같이 숫자로 된 긴 식별자를 짧게 줄일 때 유용
ex)alert( 123456..toString(36) ); // 2n9c
점을 두개 쓴 건 오타가 아니다. 숫자를 대상으로 toString 메서드를 직접 호출하려면 숫자 다음에 점 두개를 붙여야한다. 하나만 붙이면 그 점을 소수점으로 인식하게 된다...
점을 두개 쓰면 자바스크립트는 소수부가 없다고 생각하여 함수를 호출한다!

(parseInt(str, base)를 사용하면 str을 base 진수로 바꿔준다. 단 base는 진수를 의미하기 때문에 2 <= base <= 36 이어야 한다.)

어림수 구하기

어림수 관련 내장 함수는 대표적으로 아래와 같은 종류가 있다.

Math.floor
소수점 첫째 자리에서 내림(버림). 3.1은 3, -1.1은 -2
(왜 -1.1에서 0.1을 내리면 -2가 되는 걸까?? 3은 양수고 3보다 3.1이 큰 수니까 내려도 3이 된다. -1.1은 음수고 -1.1은 -1보다 더 작은 수다. 여기서 더 내리면 더 작은 수인 -2가 된다. 정신차리자.)

Math.ceil
소수점 첫째 자리에서 올림. 3.1은 4, -1.1은 -1

Math.round
소수점 첫째 자리에서 반올림. 3.1은 3, 3.6은 4, -1.1은 -1

Math.trunc (Internet Explorer에서는 지원하지 않음)
소수부를 무시. 3.1은 3이 되고 -1.1은 -1

만약 소수가 있는데 소수점 n번째 자릿수까지만 남겨 특정 숫자를 만들고 싶은 경우는?
1. 곱하기와 나누기를 이용하는 방법
2. 소수점 n번째 수까지의 어림수를 구한 후 이를 문자형으로 반환해주는 toFixed(n)을 이용하는 방법이 있다.

곱하기와 나누기

<script>
let num = 1.23456; //이 숫자를 1.23으로 만드려고 함.

alert( Math.floor(num * 100) / 100 ); // 1.23456 -> 123.456 -> 123 -> 1.23
</script>

100을 곱한 숫자에서 소숫점 자리를 다 버리고 다시 100으로 나눠 소숫점을 두번째에 찍히게 한다.

toFixed(n)사용
toFixed는 Math.round와 유사하게 가장 가까운 값으로 올림 혹은 버림한다.
주의! toFixed의 반환 값은 문자열이다! 따라서 소수부의 길이가 인수보다 작을 경우 끝에 '0'을 추가한다.
물론 이 문자열은 +단항연산자나 Number()를 이용하여 숫자형으로 변환할 수 있다.
ex) +num.toFixed(5), Number(num.toFixed(5))

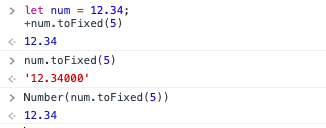
toFixed 예시)

<script>
  let num = 12.34;
  alert( num.toFixed(1) ); // "12.3", 버림

  let num = 12.36;
  alert( num.toFixed(1) ); // "12.4", 올림

  let num = 12.34;
  alert( num.toFixed(5) ); 
  // "12.34000", 소수부의 길이를 5로 만들기 위해 0이 추가됨
</script>

부정확한 계산

숫자는 내부적으로 64비트 형식 IEEE-754(IEEE에서 개발한 컴퓨터에서 부동소수점을 표현하는 가장 널리 쓰이는 표준)으로 표현되기 때문에 숫자를 저장하려면 정확히 64비트가 필요합니다. 64비트 중 52비트는 숫자를 저장하는 데 사용되고, 11비트는 소수점 위치를(정수는 0), 1비트는 부호를 저장하는 데 사용됩니다.
위에서 설명한 부호를 저장하는 1비트 덕분에 0을 포함한 모든 숫자에 부호를 붙일 수 있고 0도 -0으로 쓸 수 있다.
근데 -0은 모양만 다르지 그냥 0과 동일하게 취급한다.
숫자가 너무 커지면 64비트 공간이 넘쳐서 Infinity로 처리됩니다.
alert( 1e500 ); // Infinity

Infinity 외에 정밀도 손실(loss of precision) 문제도 있다.

<script>
	alert( 0.1 + 0.2 == 0.3 ); // false
    alert( 0.1 + 0.2 ); // 0.30000000000000004
</script>

정말 어이가 없다.
왜 이런 연산이 일어날까???

숫자는 0과 1로 이루어진 이진수로 변환되어 연속된 메모리 공간에 저장된다.
따라서... 0.1, 0.2 같은 소수들을 10진법으로 표현하면 문제가 없지만 이진법으로 표현하면 무한소수가 된다.
10진법 체계에서는 0.1(= 1/10), 0.2(= 2/10) 이런 수들이 잘 동작하겠지만 2진법 체계에서는 2의 거듭제곱으로 나눈 값들만 잘 동작한다.

10진법에서 1/3을 정확히 나타낼 수 없듯이, 2진법을 사용해 0.1 또는 0.2를 정확하게 저장하는 방법은 없다.

IEEE-754에선 가능한 가장 가까운 숫자로 반올림하는 방법을 사용해 이런 문제를 해결한다.
반올림 규칙을 적용하면 '작은 정밀도 손실’을 가릴 수 있지만 실제로는 손실이 발생된다.
toFixed를 사용하면 위 정밀도 손실을 확인할 수 있다.
alert( 0.1.toFixed(20) ); // 0.10000000000000000555

자바, C, Ruby 등에서도 같은 숫자형식을 사용하여 같은 결과를 얻는다고 한다.

소수점 끝자리에 0을 붙이고 싶으면 toFixed를 사용하면 유용하다.
문자열이라서 끝에 0이 와도 다 출력된다.

숫자에 임시로 100(또는 더 큰 숫자)을 곱하여 정수로 바꾸고, 원하는 연산을 한 후 다시 100으로 나누는 것도 하나의 방법이 될 수 있다. 하지만 결국 마지막 연산이 나눗셈이기 때문에 다시 소수를 만나게 된다...^^

정밀도 손실을 '완벽하게' 할 수 있는 방법은 없다!!!
손실을 완벽하게 하는 게 아니라 소수를 잘라서 완벽해 보이게 한다.

기가막힌 예시)

<script>
  alert( 9999999999999999 ); // 10000000000000000이 출력된다.
</script>

위의 예시는 또 왜이럴까? 마찬가지로 정밀도 손실 때문이다.
숫자를 담는 공간인 52비트짜리 공간은 위 숫자를 담기에는 부족하다.
자바스크립트는 숫자 손실이 일어나도 오류를 발생시키지 않고 적절하게 보여주려고 최선을 다한다... 그래서 노력의 결과로 다른 값을 보여준다.

isNaN과 isFinite

Infinity와 -Infinity : 그 어떤 숫자보다 큰 혹은 작은 특수 숫자 값
NaN : 에러를 나타내는 값

위 세 값은 숫자형에 속하지만 정상적인 숫자가 아니다. 따라서 위 값들과 정상적인 숫자를 구분하기 위한 함수가 존재한다.

<isNaN(value)>

인수를 숫자로 변환한 다음 NaN인지 테스트한다.

<script>
  alert( isNaN(NaN) ); // true
  alert( isNaN("str") ); // true
</script>

왜 굳이 n===NaN 이렇게 비교하지 않고 isNaN 함수를 쓸까?
NaN은 자기 자신과도 같이 않기 때문이다. (정말 골때리는 형식이 다 있다)
NaN === NaN 은 false를 반환한다.

<isFinite(value)>
인수를 숫자로 변환하고 변환한 숫자가 NaN, Infinity, -Infinity가 아닌 일반 숫자일 경우 true를 반환한다.

<script>
  alert( isFinite("15") ); // true
  alert( isFinite("str") ); // false, NaN이기 때문.
  alert( isFinite(Infinity) ); // false, Infinity이기 때문.
  
  let num = +prompt("숫자를 입력하세요.", '');

  // 숫자가 아닌 값을 입력하거나 Infinity, -Infinity를 입력하면 false 출력.
  alert( isFinite(num) );
</script>

주의! 빈 문자열이나 공백만 있는 문자열은 모든 숫자 관련 내장함수에서 0으로 취급된다. (그동안 null로 인식되지 않을까 생각했다.)

Object.is로 비교하기
Object.is는 ===처럼 값을 비교할 때 사용되는 내장 메서드인데 예외 경우가 좀 있다.
1. NaN을 대상으로 비교할 때: Object.is(NaN, NaN) === true
2. 0과 -0이 다르게 취급되어야 할 때: Object.is(0, -0) === false
숫자를 나타내는 비트가 모두 0이더라도 부호를 나타내는 비트는 다르므로 0과 -0은 사실 다른 값이긴 하다.

위 두가지 상황을 제외하고는 Object.is(a, b)와 a === b의 결과는 같다.

parseInt와 parseFloat

단항 덧셈 연산자 + 또는 Number()를 사용하여 숫자형으로 형 변환을 할 때 피연산자가 숫자가 아니면 형 변환에 실패한다.

만약 문자열에 숫자가 혼용되어 쓰인 경우 문자열 안의 숫자를 얻기 위해서는?
parseInt와 parseFloat을 사용한다.

두 함수는 불가능할 때까지 문자열에서 숫자를 읽어오고 숫자를 읽는 도중 오류가 발생하면 이미 수집된 숫자를 반환한다.
parseInt는 정수, parseFloat는 부동 소수점 숫자를 반환한다.

<script>
  alert( parseInt('100px') ); // 100
  alert( parseFloat('12.5em') ); // 12.5

  alert( parseInt('12.3') ); // 12, 정수 부분만 반환.
  alert( parseFloat('12.3.4') ); // 12.3, 두 번째 점에서 숫자 읽기를 멈춘다.
</script>