Graph란

단순히 생각해 여러 점들이 선으로 연결되어 있는 대부분의 것을 Graph라고 할 수 있다. 일상생활에서 우리가 쉽게 접하는 지하철노선도가 그 예시가 될 수 있을 것이다. 앞선 글에 있던 Tree보다는 좀 더 general한 개념이며, Tree가 Graph의 일종이라고 볼 수 있다.(다만 Tree는 hierarchical한 성격을 띈다.)

Terms

• Vertex
  우리가 쉽게 Node라고 부르는 '점'에 속하며, Graph에서는 vertex, vertices라는 표현을 사용한다.

• Edge
  (v, w)와 같이 a pair of vertices로 표현되며 두 vertices간의 연결관계를 뜻한다. Edge는 방향을 가질 수 있으며, 모든 Edge가 방향을 갖는 그래프를 Directed Graph라고 한다.
  두 vertex가 adjacent하다는 의미는 Edge로 연결되어 있다는 것과 동치이며, 이 경우 한 vertex를 나머지 vertex의 neighbor라고 부르기도 한다.

• Weight
  각각 Edge에 Weight가 있을 수 있다. 단순한 예시를 들자면 도시와 도로에 대한 Graph에서 Edge의 Weight는 도시사이의 거리를 뜻할 수 있다.

• Path
  Path V to W의 경우 (v->a->b->c->w)와 같이 V vertex에서 W vertex로 가는 경로를 의미한다. Tree와 다르게 Path는 여러개가 존재할 수 있으며, 'cycle'이 있을 경우 무한하다고도 볼수 '는' 있다.
  simple path는 path내에 같은 vertex가 중복되지 않는, 'cycle'이 없는 path를 뜻한다.

• Cycle
  V에서 출발해서 다시 V로 돌아오는 것이 가능할 경우 이를 Cycle이라고 한다. 즉 (V->a->b->V)가 될 경우 이를 Cycle이라고 한다. Cycle이 하나라도 포함된 graph를 Cyclic Graph, 그렇지 않은 Graph를 Acyclic Graph라고 한다.

• Simple Graph
  Cycle(loop)가 없고 Parallel Edge(v와 w를 잇는 Edge가 2개 이상인 것)가 없는 Graph를 뜻한다.

Graph를 표현하는 방법

Graph는 일반적으로 G = (V, E)로 표현한다. V는 Graph 내부에 있는 모든 Vertices를 뜻하고 E는 Edge로 (v, w)와 같이 vertices 두 개로 구성된 tuple들의 모임이다.

Adjacency Matrix

row와 column 모두 하나의 vertex를 의미하며 따라서 vertex가 N개이면 (N x N) matrix가 된다. (v, w)의 원소는 v에서 w로 가는 edge의 유무를 뜻하면 1이면 존재, 0 이면 없음이다.
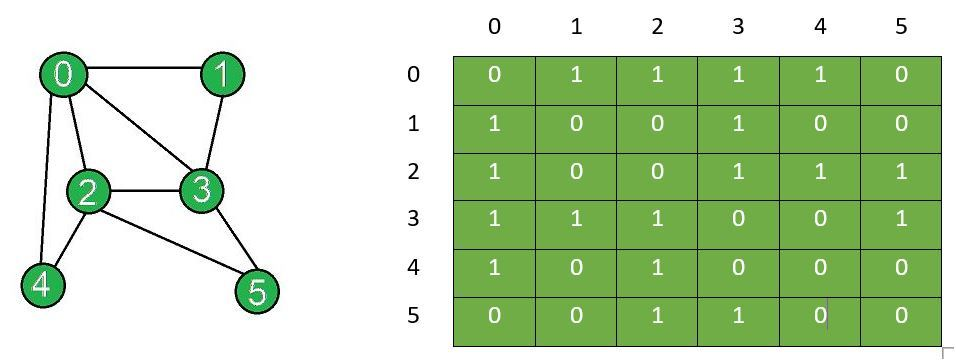(출처 : geeksforgeeks)

• 매우 간단한 방식이며 한눈에 Graph의 대략적인 생김새를 파악할 수 있다.
• Edge가 많을 경우 Graph를 표현하기 용이하다.
• 그러나 대부분의 경우 Edge가 그다지 많지 않아 대부분의 원소가 0 이다.

따라서 현실적으로 잘 쓰이지는 않는다.

Adjacency List

각 vertex 마다 어떤 vertex와 연결되었는지를 표시하는 방식이다.

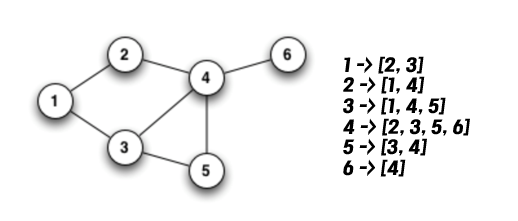
• space-efficient way이다. (Edge가 없음을 표현할 필요가 없다.)
• sparse한 graph를 표현하기 좋다
• vertex의 관점에서 주변 vertex들과의 관계를 확인하기 수월하다.

Graph 구현

Graph의 경우 구현하는 방식이 여러가지 있을 것이다. 애초에 Vertex를 새로운 class로 만들어 구현할 수 도 있을 것이고, 단순 Graph class 하나로 표현할 수도 있을 것이다. 여기서는 아주 간단한 Undirected Graph(Edge가 방향을 갖고있지 않음) 구현을 해보았다.

class UndiGraph:
    
    def __init__(self, V, E):
        self.V = set(V)
        self.adj_list = {}
        for v in V:
            self.adj_list[v] = []
        for v, w in E:
            self.adj_list[v].append(w)
            self.adj_list[w].append(v)
            
    def addVertex(self, name):
        if name in self.V:
            print(str(name) + 'is already exist')
        else:
            self.V.add(name)
            self.adj_list[name] = []
            
    #파라미터 명이 f(from), t(to) 이기는 하지만 is undirected이기에
    #양쪽으로 Edge를 만들어준다고 생각해야한다.
    def addEdge(self, f, t):
        self.adj_list[f].append(t)
        self.adj_list[t].append(f)
        
    def getNeighbors(self, name):
        if name in self.V:
            return self.adj_list[name]
        else:
            return None

이어서 나올 탐색에 관한 글에는 아래 예시 Graph를 기준으로 진행한다.

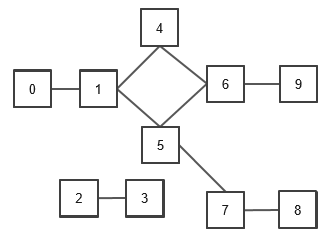
BFS

Tree 글에서도 나왔었던 BFS이다. 상단의 Graph class 내부 method로 구현했으며, Tree에서와 어떤 차이점이 있는지 알아보자.

    # 이 파트는 참 애매하다고 생각한다. Tree는 root가 있기에 그 점에서 시작하면 되지만
    # Graph는 특정한 점이 없어 여기선 시작지점을 직접 넣는 것으로 코드를 작성하였다.
    def BFS(self, start):
        if not start in self.V:
            print('Input Vertex is not in Graph')
            return None
        else:
            visited = {vertex:False for vertex in self.V}
            q = [start]
            while q:
                curr = q.pop(0)
                if not visited[curr]:
                    visited[curr] = True
                    print(curr)
                    q += self.getNeighbors(curr)   

중간에 등장하는 visited가 Graph와 Tree에서의 가장 큰 차이라고 할 수 있다. Graph에는 cycle이 존재할 수 있기 때문에 edge를 따라 가다보면 이미 방문했던 Vertex를 재방문하게 될 수도 있다. 이를 방지하고자 visited라는 변수를 설정하여 방문여부를 따로 관리한다.
나머지 부분은 Tree와 유사하다. q에 있는 vertex들을 하나씩 방문하며, 해당 vertex의 neighbor을 다시 q에 주입해준다. q를 FIFO으로 사용하고 있기 때문에 Breadth-First한 탐색이 가능한 것이다.

시행해본 결과는 아래와 같다.
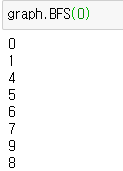현재 구현에서는 모든 vertex를 방문하는게 아닌 시점에서부터의 탐색을 목적으로 구현하여 [2, 3] vertex들은 방문되지 않았다.

DFS

DFS 또한 tree에서와의 큰 차이점은 visited를 두어 방문여부를 관리한다는 점이다. DFS에는 preorder, inorder, postorder 세가지가 있었지만 결국 하나를 작성할줄 안다면, 세 가지의 차이점은 방문을 언제시키냐(아래 코드에선 print(start))의 문제이므로, inorder 코드는 작성하지 않았다. 또한 아래 코드는 Recursion을 이용하였지만 stack을 통해서도 구성할 수 있다!

    def DFS(self, start, order):
        visited = {vertex:False for vertex in self.V}
        if order == 'pre':
            self.__DFS_preorderHelp(visited, start)
        elif order == 'post':
            self.__DFS_postorderHelp(visited, start)
        else:
            print('적절한 order를 넣어주세요')
            
    def __DFS_preorderHelp(self, visited, start):
        if not visited[start]:
            visited[start] = True
            print(start)
            for v in self.getNeighbors(start):
                self.__DFS_preorderHelp(visited, v)
            
    def __DFS_postorderHelp(self, visited, start):
        if not visited[start]:
            visited[start] = True
            for v in self.getNeighbors(start):
                self.__DFS_postorderHelp(visited, v)
            print(start)

구현은 recursive하게 진행하였다. 이해를 쉽게 하기 위해선 각 vertex가 세가지 상태를 가질 수 있다고 생각하면 편하다.

1. 아예 방문되지 않은 vertex
2. 해당 vertex는 방문됐지만, neighbor들의 방문이 끝나지 않은 경우
3. 자신과 자신의 neighbor 모두 방문이 끝난 경우

preorder의 경우 1번에서 2번이 되었을 때 print가 된다고 생각하면 된다. 따라서 각 vertex가 최초 방문되었을 때 print된다.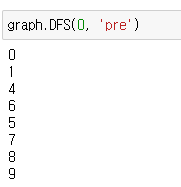
postorder의 경우 2번에서 3번이 되었을 때 print 된다고 생각하면 된다. 즉 끝까지 탐색하고 돌아오는 과정에서 print된다.

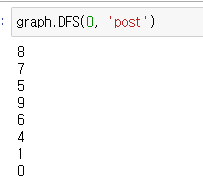
BFS와 DFS는 주어지는 상황에 따라 적절하게 사용할 수 있다면 문제를 해결하는데 꽤나 도움이 될 것이다.(아직 나도 잘 하지는 못한다...)

구글에 검색해보면 많은 사람들이 그래프의 BFS, DFS에 대해 자신의 코드를 설명하고 있는데, 댓글들을 보면 작성자의 구현이 틀렸다고 얘기하는 사람들이 종종 있다. 내가 보기에 그들은 BFS(BFT)와 DFS(DFT)를 알고리즘으로 착각하여 그러는 것같다. 이 두가지는 알고리즘이라기 보다는 방법론에 좀 더 가깝다고 생각한다. 따라서 그 원리를 충분히 이해하여 코드를 작성한다면 동일한 input에 대해 output이 다르더라도, 그저 자신의 규칙이 있는 코드인 것이다.
결국 BFS, DFS의 핵심인 '너비와 깊이'만을 이해하고 기억하면 된다.

마치며

Graph에 대한 개략적인 내용을 정리하는 것으로 자료구조와 알고리즘에 대한 기본적인 내용은 마무리 된 것같다. 공부를 하면서도 아직 많이 부족한게 느껴진다. 긍정적인 부분이라면 무분별하게 사용하던 Recursion에 대해 조금은 익숙해져 가는 느낌이다. 이후로는 코딩 문제들을 풀어보며 공부한 내용을 체화시켜볼 예정이다!