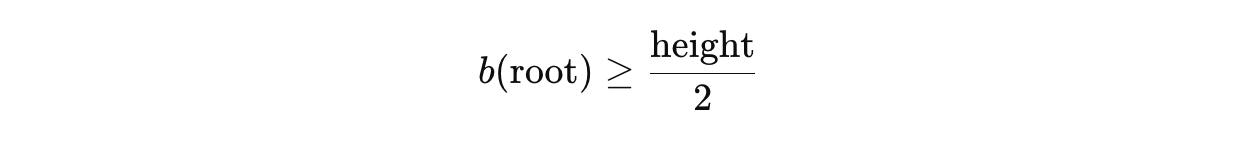이전 시간까지 우리는 다양한 정렬 알고리즘에 대해서 공부했다.
지금부터는 자료구조를 기반으로한 다양한 알고리즘에 대해 알아보자.

그 중에서도 이번 시간엔 BST (Binary Search Tree), 특히 Red-Black Tree를 배워볼 것이다.

🌲 Why are we studying BSTs?

✅ 1. 핵심 포인트

컴퓨터 과학에서 가장 중요한 주제 중 하나는 데이터의 저장과 검색 (Storage and Retrieval) 이다.

✅ 2. BST는 빠른 저장 및 검색을 가능하게 해준다

BST는 데이터를 정렬된 상태로 유지하면서도 다음과 같은 연산들을 빠르게 처리할 수 있다. (단, 트리가 균형 잡혀 있을 경우)

INSERT, DELETE, SEARCH ∈ O(logn)

✅3. Red-Black Tree는 좋은 아이디어다

Red-Black Tree와 같은 균형 이진 탐색 트리는
항상 트리의 높이를 O(logn)으로 유지하기 위한 똑똑한 전략을 사용한다

그래서 이런 구조를 배우는 건, 논리적인 아이디어와 문제 해결 방식을 접하는 좋은 경험임.

---

🧩 Sorted Array

정렬된 배열에서의 연산과 시간복잡도는 다음과 같다.

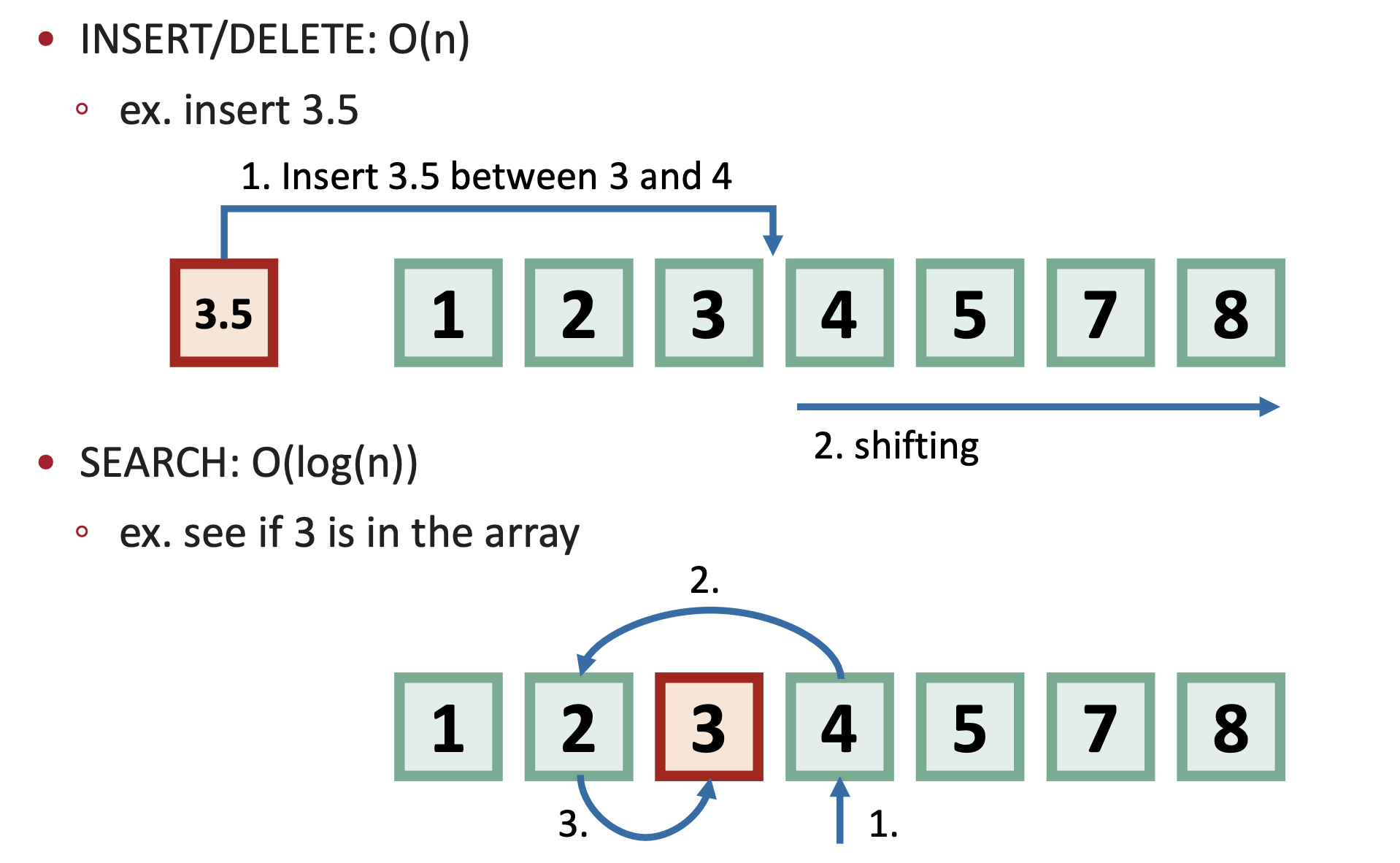
📌 삽입(INSERT) / 삭제(DELETE)

시간 복잡도: O(n)

이유: 삽입/삭제 위치는 이진 탐색으로 빠르게 찾을 수 있지만,
그 위치 이후의 모든 원소를 밀거나 당겨야 하기 때문에 최악의 경우 $n$개의 요소 이동이 필요함.

🔍 탐색(SEARCH)

시간 복잡도: O(logn)
이유: 배열이 정렬되어 있으므로 이진 탐색(Binary Search) 사용 가능하며 절반씩 Divide하기 때문

---

🧩 Linked List

반면, 연결리스트에서의 연산과 시간복잡도는 다음과 같다.

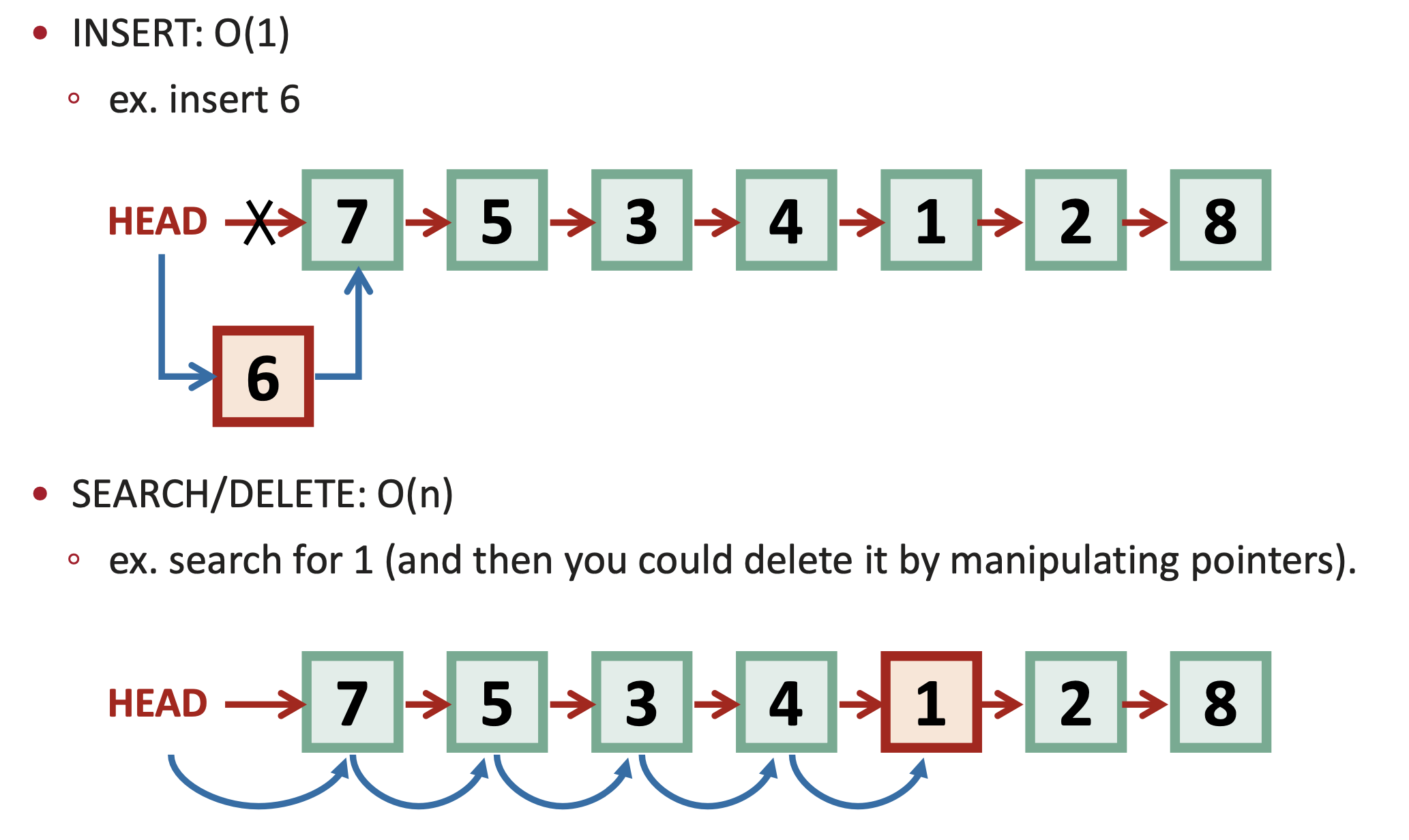
✅ 삽입 (INSERT)

시간복잡도: O(1)
이유: 새로운 노드를 리스트 앞에 그냥 끼워 넣으면 되므로 포인터 2개만 바꾸면 끝이다.

❌ 탐색 / 삭제 (SEARCH / DELETE)

시간복잡도: O(n)
이유: 연결 리스트는 인덱스로 접근할 수 없기 때문에, 맨 앞부터 순차적으로 탐색해야 한다.

---

Motivation For BSTs

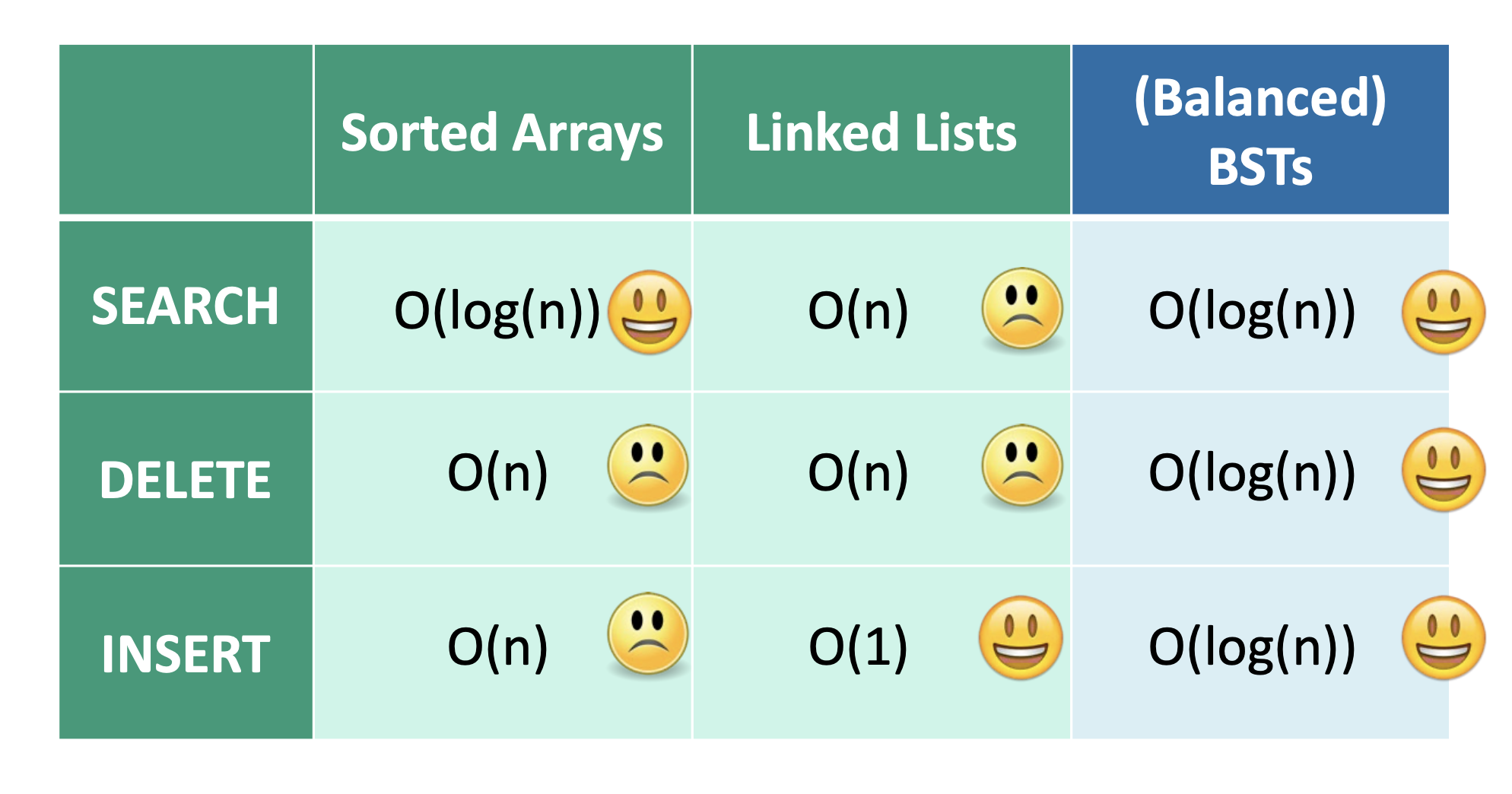정렬된 배열과 연결리스트의 연산 중 최악의 경우, O(n)이 걸리는 것을 알 수 있다.
문제점을 알았으니 모든 경우에서도 O(logn)이 걸리는 BST를 안 배우면 안되겠지요?

---

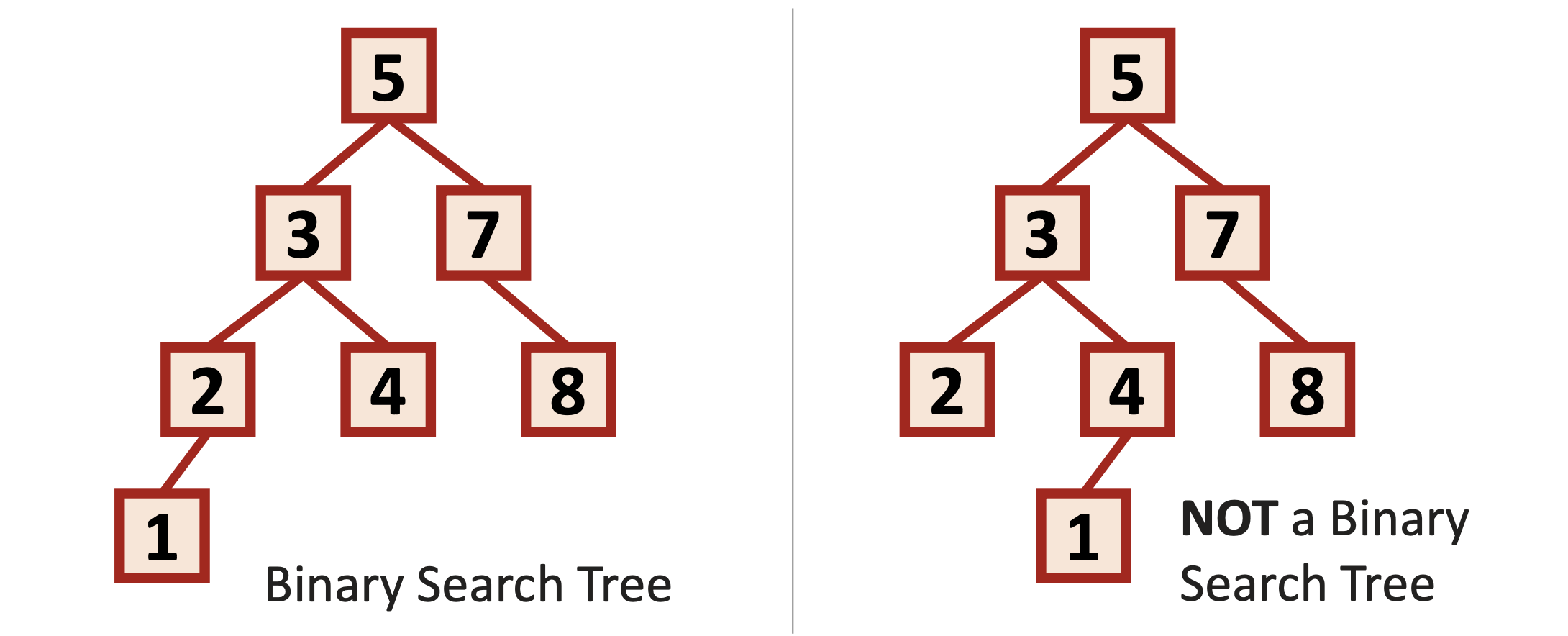
🧠 Binary Search Tree (BST)란?

📌 정의: BST는 이진 트리 중에서 다음 조건을 만족하는 트리를 말한다.

왼쪽 서브트리의 모든 값은 부모 노드보다 작아야 함
오른쪽 서브트리의 모든 값은 부모 노드보다 커야 함

기존의 이진트리의 속성을 모두 가지면서 모든 노드에 대해 위 조건을 만족하는 트리를 의미한다!

---

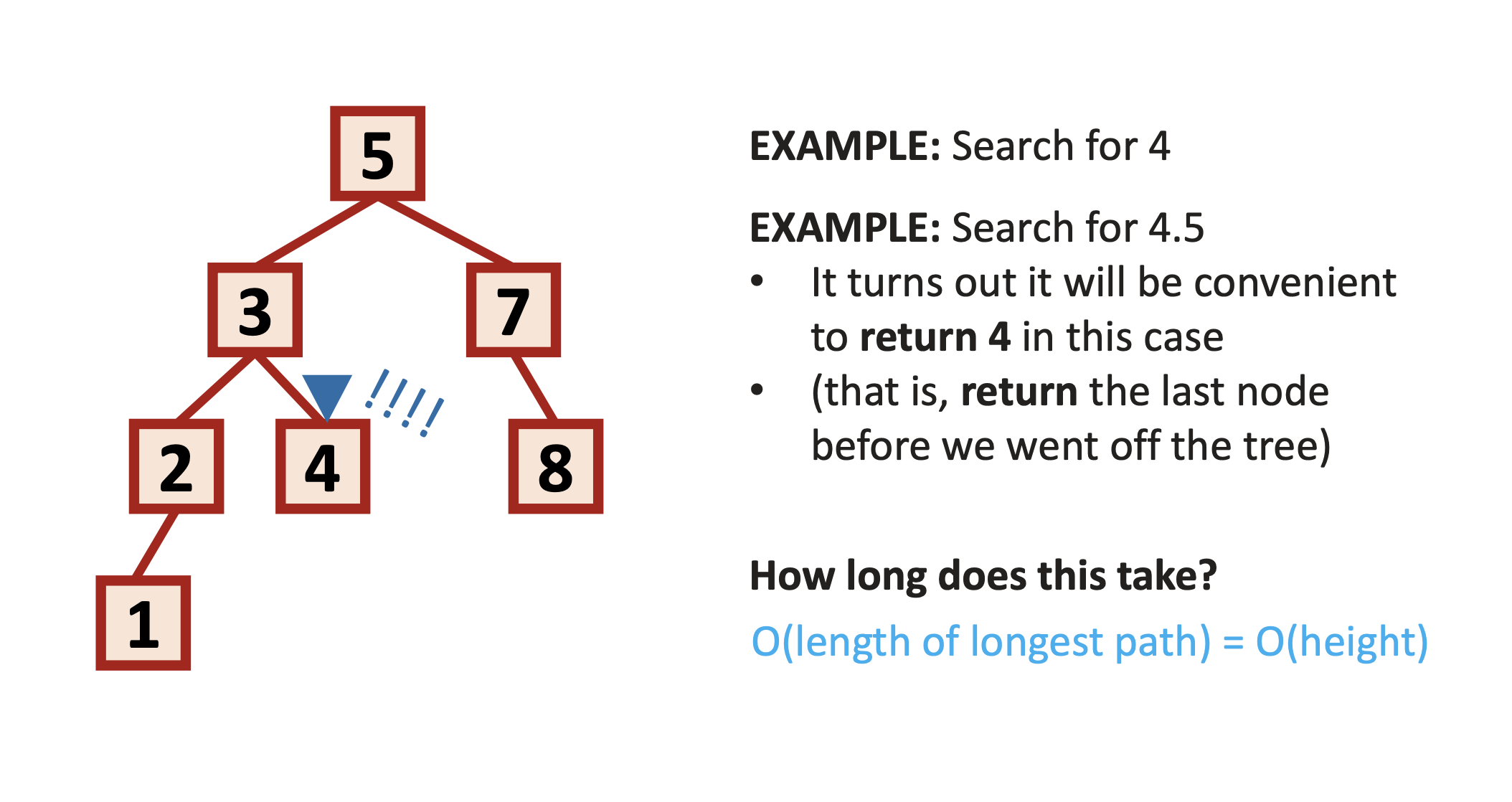
🔍 SEARCH in BSTs

⏱️ 시간복잡도

BST에서 탐색은 트리의 루트부터 리프까지 가는 경로 중 하나를 따르므로,
최악의 경우는 트리의 높이(Height) 만큼 탐색해야 한다.
따라서 시간복잡도는 O(h) (균형 잡힌 트리라면 O(log n), 편향되면 최악의 경우 O(n))

✅ INSERT in BSTs

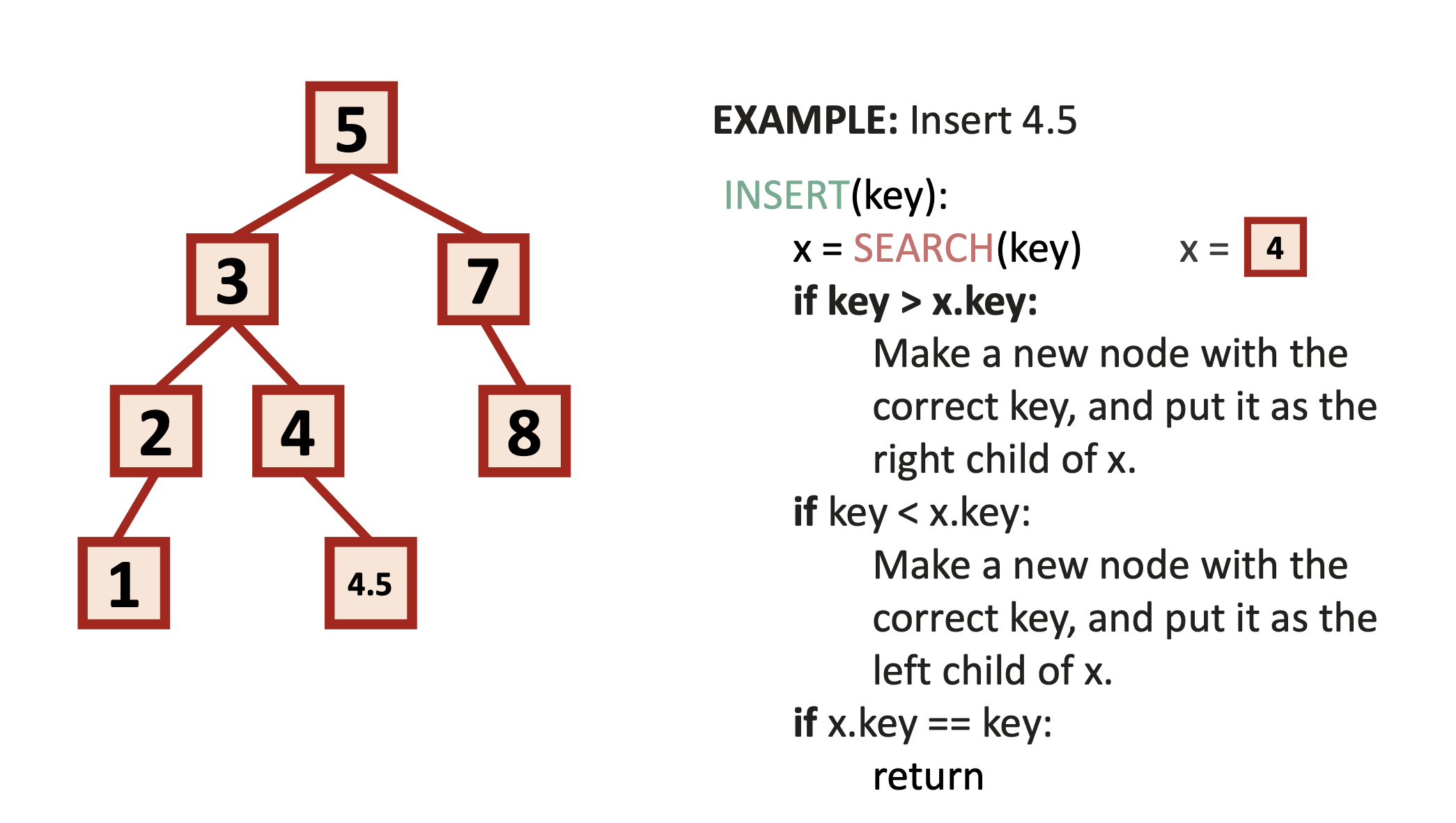
1️⃣ 먼저 SEARCH로 적절한 위치 탐색

SEARCH(4.5) → 마지막으로 도달한 노드는 4

2️⃣ 삽입 조건 분기

if key > x.key: 오른쪽 자식으로 삽입
if key < x.key: 왼쪽 자식으로 삽입
if key == x.key:
이미 있음 → 삽입 안 함

✅ 실제 동작 흐름

4.5는 4보다 크니까 → 4의 오른쪽 자식으로 삽입 (새로운 노드 4.5 생성하여 붙임)

⏱️ 시간복잡도

BST에서 삽입 또한 탐색이 필요하므로 삽입도 결국 트리의 높이만큼 걸린다
따라서 시간복잡도는 균형 잡힌 트리라면 O(log n), 편향되면 최악의 경우 O(n)

---

❌ DELETE in BSTs

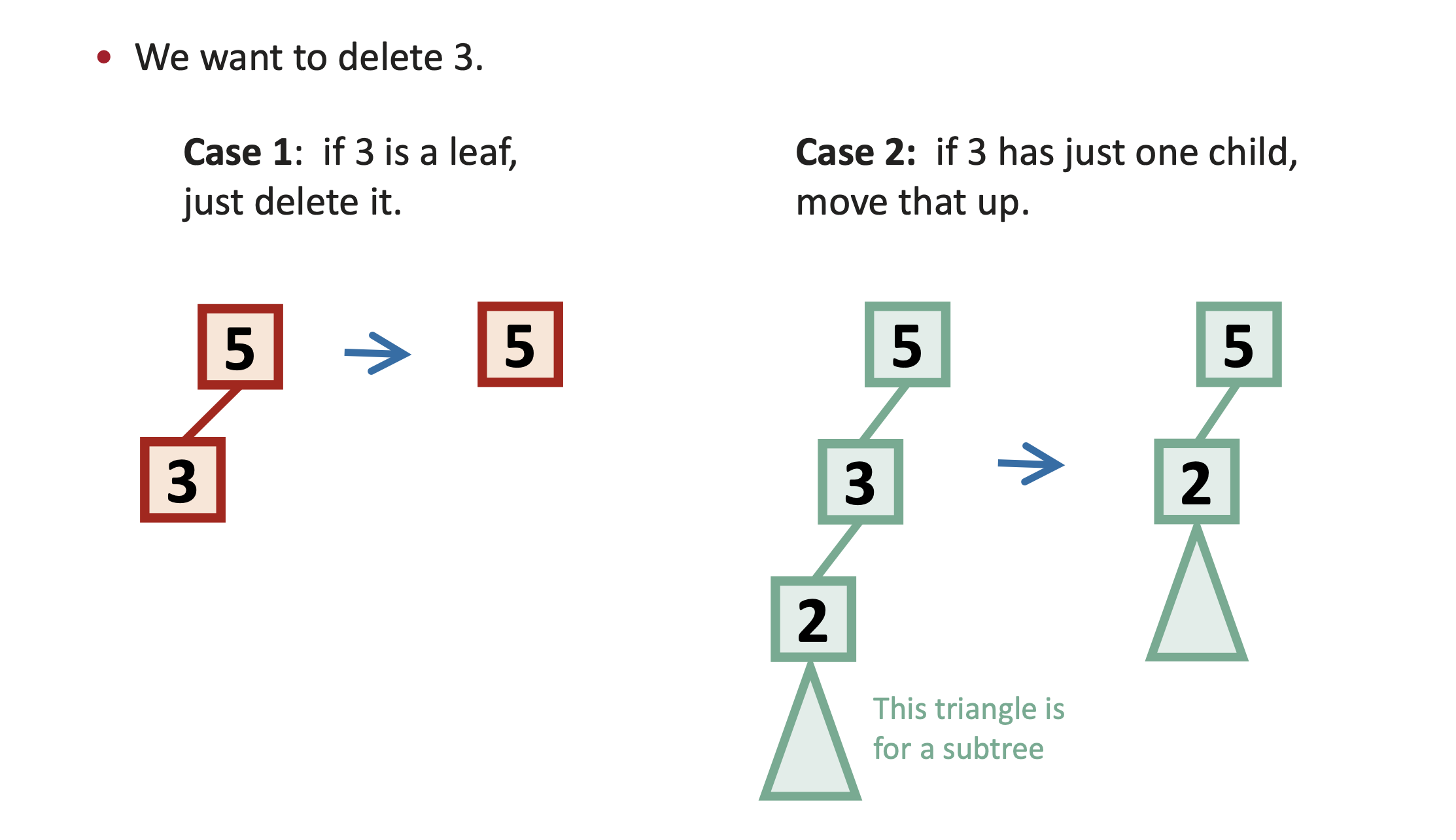
🌳 Case 1: 삭제할 노드가 리프(leaf)

삭제할 노드가 자식이 하나도 없다면 그냥 제거하면 된다

🌳 Case 2: 삭제할 노드가 자식이 하나 있음

자식이 하나뿐인 경우 → 그 자식을 위로 올리면 된다

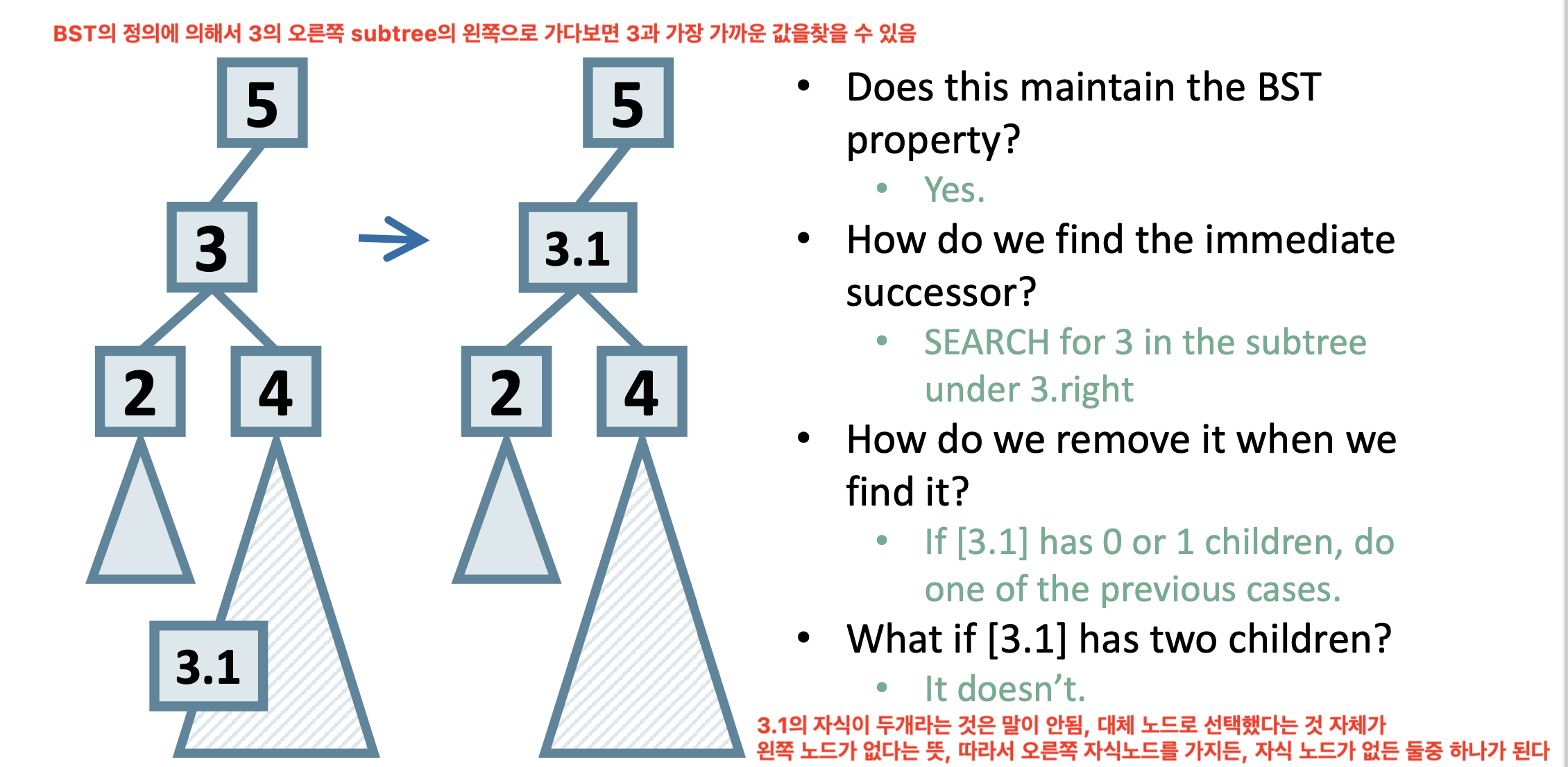
🌳 Case 3: 삭제할 노드가 두 개의 자식을 가지는 경우

✅ 해결 방법:
3을 그 다음으로 큰 값(immediate successor) 으로 대체하면 된다.

사진에서처럼 3의 오른쪽 서브트리에서 가장 왼쪽에 있는 노드를 찾으면
그게 바로 "immediate successor"이다

⏱️ 시간복잡도

BST에서 삭제 또한 탐색이 필요하므로 삽입도 결국 트리의 높이만큼 걸린다
따라서 시간복잡도는 균형 잡힌 트리라면 O(log n), 편향되면 최악의 경우 O(n)

---

Height Problem

앞서 모든 연산에서 말했듯이, 이진탐색트리가 편향되면 시간 복잡도는 늘어난다.
이를 해결하기 위한 몇가지 아이디어를 생각해보자

🧠 Idea 0 (초기 아이디어)

높이를 계속 추적하다가 너무 커지면 트리를 아예 다시 만들어버리자!

⛏️ 전략 요약

• 트리의 깊이(height)를 추적하다 너무 깊어지면 → 전부 다시 짠다 (rebuild)
• 최소한 $Ω(n)$마다 한 번씩은 해야 할 수도 있기에 썩 좋은 아이디어는 아니다.
  

나가~

🧠 Idea 1: Rotations

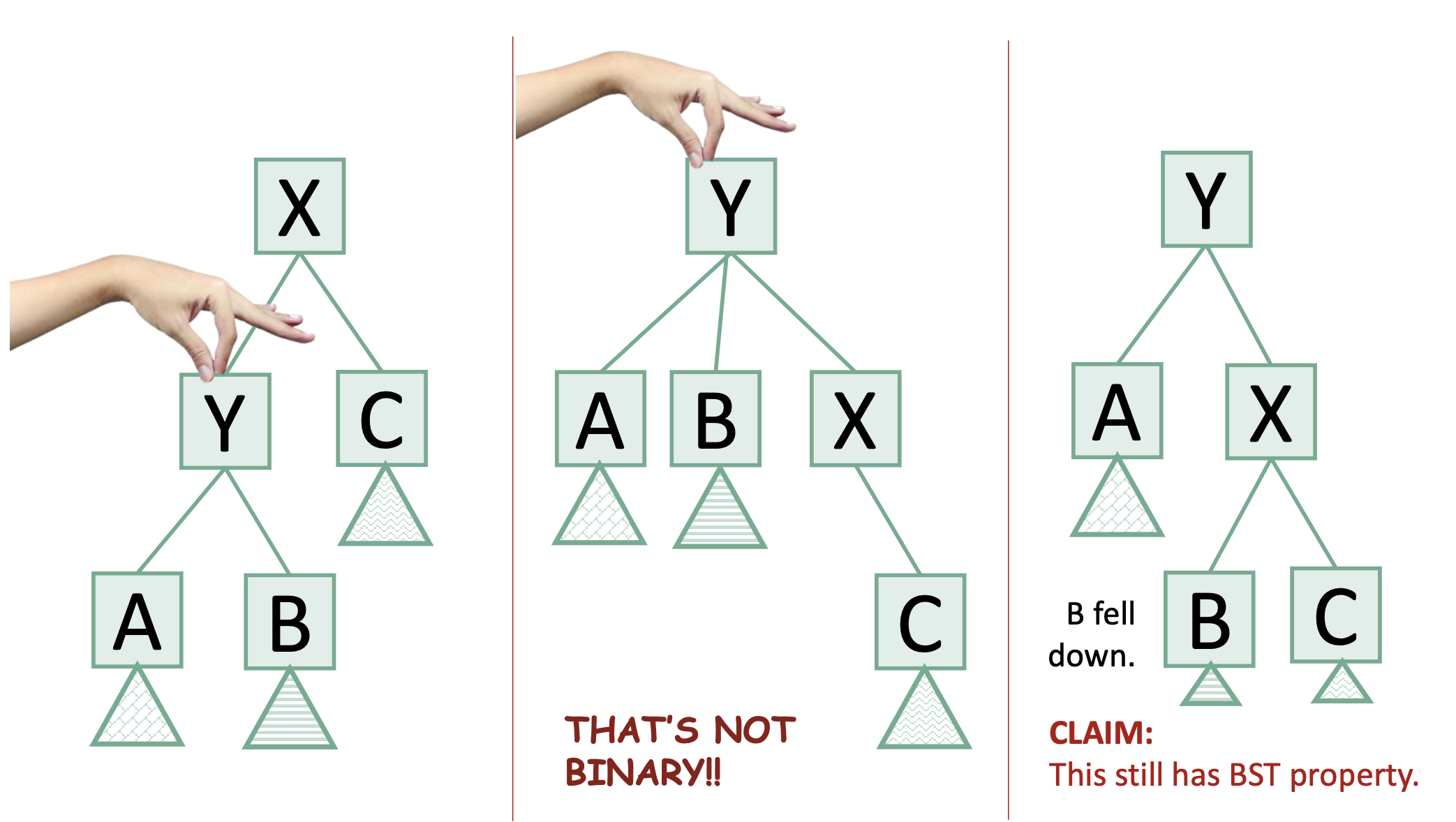
BST의 성질을 깨뜨리지 않으면서도, 노드들의 위치를 회전시켜서 트리의 높이를 줄이거나 균형을 맞춘다!

✅ 회전의 목적

• 높이 줄이기: 높이를 줄이면 탐색 시간이 줄어듦
• 균형 맞추기: 특정 서브트리에 너무 치우치지 않도록

🤔 하지만 이건 너무 애매하지

도대체 언제 불균형이라고 하고, 뭘 기준으로 괜찮다고 판단하는가?

이를 해결하기 위해, 우린 Red-Black Tree에 대해 배워 볼 것이다

---

🔴⚫ Red-Black Tree

Red-Black 트리는 다음과 같은 규칙을 가진다

1. 각 노드는 빨강(Red) 또는 검정(Black)

→ 트리에 있는 모든 노드는 색깔을 갖고 있다.

2. 루트 노드는 항상 검정색(Black Node)

→ 트리의 루트는 반드시 검정이어야 한다.

3. 모든 NIL 자식(leaf로 간주됨)은 검정색으로 간주

→ 실제로 존재하지 않는 자식(null 포인터)도 검정으로 생각한다.

4. 빨간 노드의 자식은 반드시 검정 노드여야 함

→ Red 노드 밑에 또 Red 노드가 올 수 없다. (Red는 연속 불가!)

5. 어떤 노드 x에서 NIL로 가는 모든 경로는 동일한 수의 검정 노드를 거쳐야 함

→ 이게 핵심 균형 조건입니다.
→ 모든 경로의 블랙 노드 수가 같아야 균형을 이룬다고 보는 것!

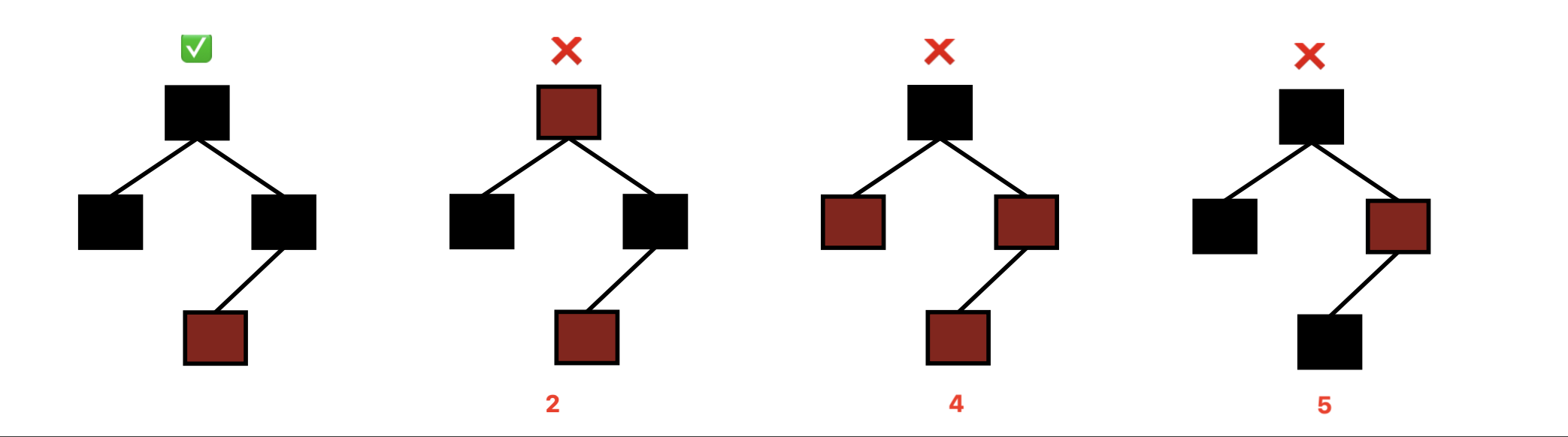
이 그림 속 첫번째 트리 빼곤 다 RB트리의 조건을 하니씩 어기고 있다.

Red-Black Tree의 규칙은 완벽한 균형을 유지하는 것보다 느슨하지만,
충분히 균형에 가까운 구조를 유지하기 위한 프락시(proxy)이다.

즉, 완전한 AVL Tree 같은 트리보단 덜 엄격하지만,
탐색 시간 O(log n)을 보장하기 위해 약간의 "균형 조건"을 설정해 놓은 것

⚫ 검정 노드(black nodes)는 균형을 만들어준다
어떤 노드에서 리프(NIL 노드)까지 가는 모든 경로는 같은 수의 black 노드를 거쳐야하므로
이 덕분에 트리가 한쪽으로 쏠리지 않음.

🔴 빨간 노드(red nodes)는 드물게 퍼져 있어야 함
빨간 노드의 자식은 반드시 검정 노드여야 하므로 빨간 노드는 절대로 연속되지 않는다
→ 트리의 깊이에 큰 영향을 주지 않게 막아주는 역할을 함.

---

How can we prove?

🔴⚫ 규칙 덕분에 트리가 너무 치우칠 수 없다!

모든 리프까지의 경로에서 검정 노드 수는 항상 같다 (black-height).
빨간 노드는 연속될 수 없기 때문에, 길이를 더 늘리려면 검정-빨강-검정-빨강... 구조로 늘리는 수밖에 없음.
그러면 어떤 경로라도 검정 노드 수의 2배 길이를 넘을 수 없다!

📏 높이 증명 직관

어떤 경로의 검정 노드 수가 bh (black-height) 라고 해보자.
그러면 전체 경로의 최대 길이는 2 × bh (검정, 빨강 번갈아 최대한 붙였을 때).
그리고 검정 노드 수는 $\ge \log(n+1)$ 이라는 성질이 있으니...

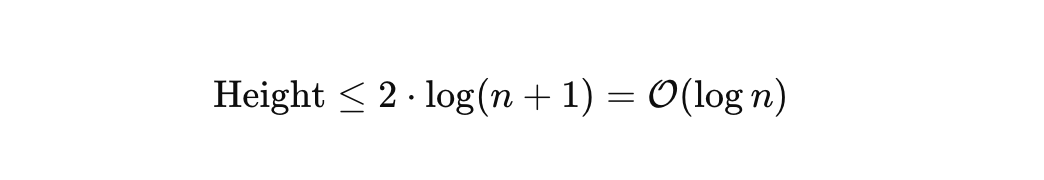
🌲 정리

레드블랙트리는 약간의 불균형을 허용하지만, 불균형이 최대 2배 이상이 되지 않게 강제함
그래서 높이는 항상 $\mathcal{O}(\log n)$, → 탐색, 삽입, 삭제도 $\mathcal{O}(\log n)$

---

용어 정의

b(x) = 노드 x에서 NIL까지 가는 모든 경로 중 black node의 수
(단, x는 포함하지 않고, NIL은 포함함, 즉, x의 아래쪽 서브트리 깊이 중에서 black node 개수)

📢 Step 1 : Claim (귀납 주장)

어떤 노드 x에 대해, x의 서브트리에는 최소 $2^b(x) - 1$ 개의 노드가 존재한다. (NIL 제외)
즉, black node 수가 많을수록 그 아래 서브트리는 더 크다는 뜻이다.

🧮 Step 2: 이 Claim을 전체 트리에 적용

루트 노드를 기준으로 하면 $n \ge2^b(root) -1$,
그리고 red-black tree의 규칙에 따라 다음이 항상 성립함:

빨간 노드는 연속으로 못 오니까, 전체 height 중 절반 이상은 black이어야 함

🔄 Step 3: 정리 (Rearranging)

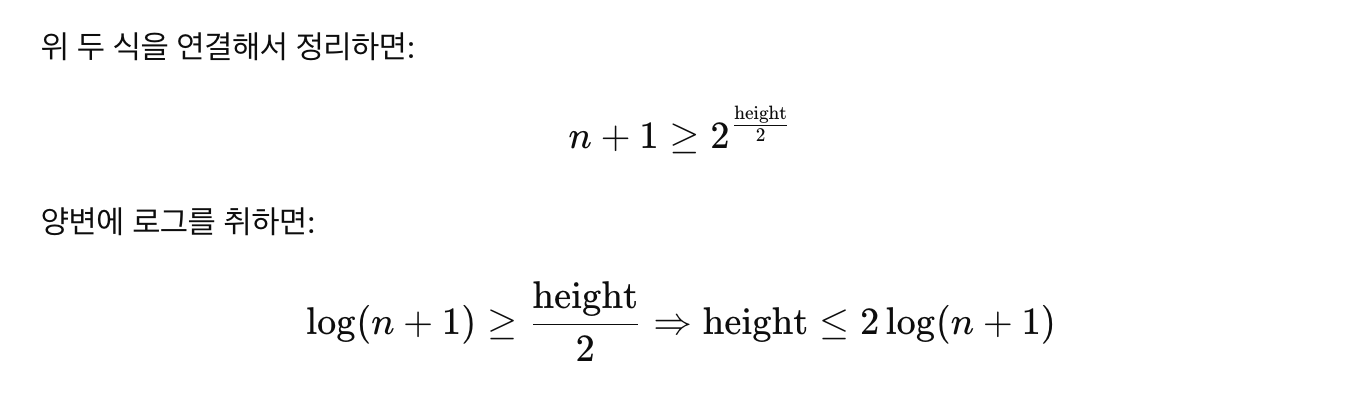
🎯 최종 결론

레드블랙 트리의 높이는 항상 $height \le 2log(n+1)$ 이므로
-> 탐색/삽입/삭제 모두 $\mathcal{O}(\log n)$ 보장!