[1스4코3파] #274. Leetcode 746. Min Cost Climbing Stairs

[1스4코3파] 1명의 스위프트 개발자와 4명의 코틀린 개발자, 3명의 파이썬 개발자코딩 테스트 서막 : 1스4코3파

START :

[3코1파] 2023.01.04~ (274일차)
[4코1파] 2023.01.13~ (266일차)
[1스4코1파] 2023.04.12~ (178일차)
[1스4코2파] 2023.05.03 ~ (156일차)
[1스4코3파] 2023.10.01 ~ (4일차)

Today :

2023.10.04 [274일차]

문제 설명

계단을 오를 때마다 필요한 cost를 담은 배열이 주어지고,
계단은 한 칸 또는 두 칸을 오를 수 있는데 그 때마다 해당 인덱스에 대한 cost가 발생한다.
주어진 cost에서 인덱스 0 또는 1에서 시작할 수 있을 때, 해당 계단의 가장 높은 층 까지 오를 때의 최소 비용을 구하라.

문제 풀이 방법

dynamic programming 문제라, 계단을 오르기 위해서 필요한 비용들을 한 번 스텝을 움직일 때, 두 번의 스텝으로 움직일때로 문제를 분할해야 한다.
먼저 주어진 cost 배열의 길이의 +1 이 해당 계단의 정점이므로,
주어진 cost 배열의 끝에 top 인덱스를 임의로 추가한다음
주어진 cost의 배열의 끝에서 각 인덱스가 한 칸 이동, 그리고 두 칸 이동 할때 필요한 cost들을 더해주면서 해당 cost를 update 한다.

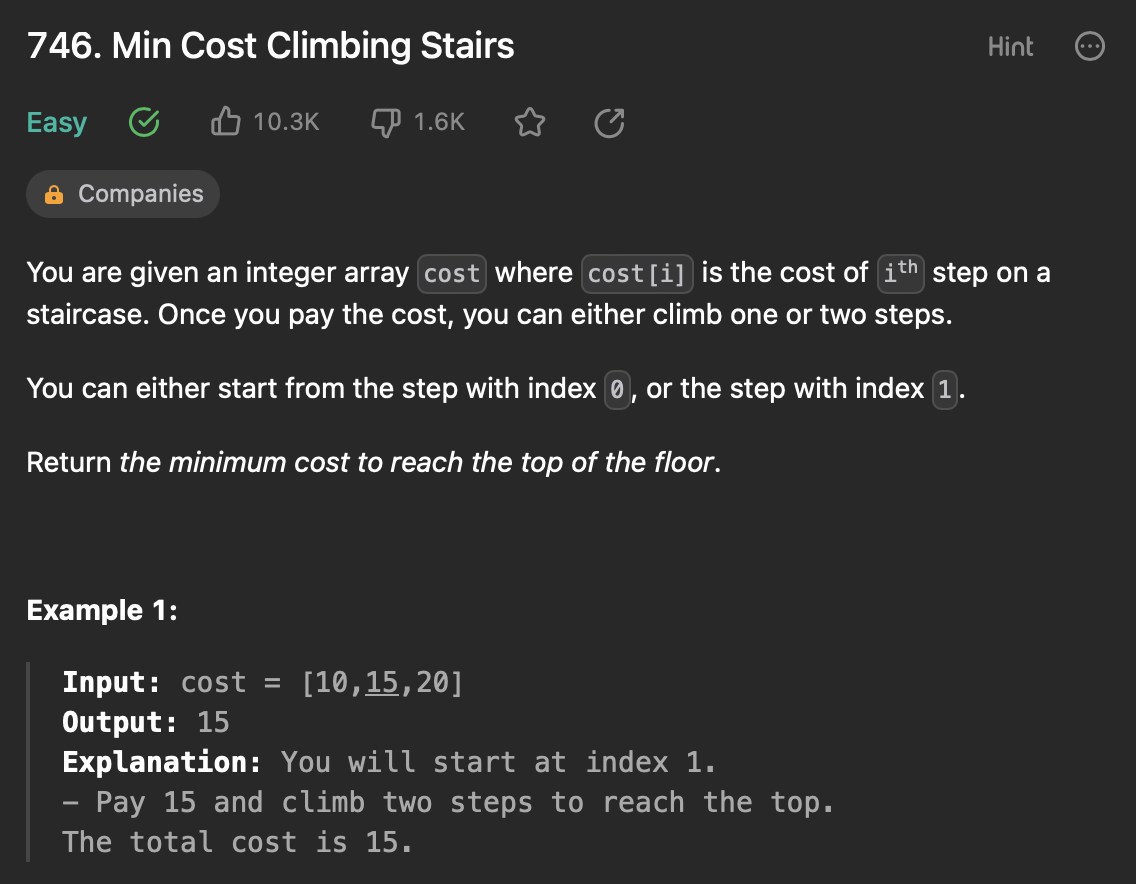
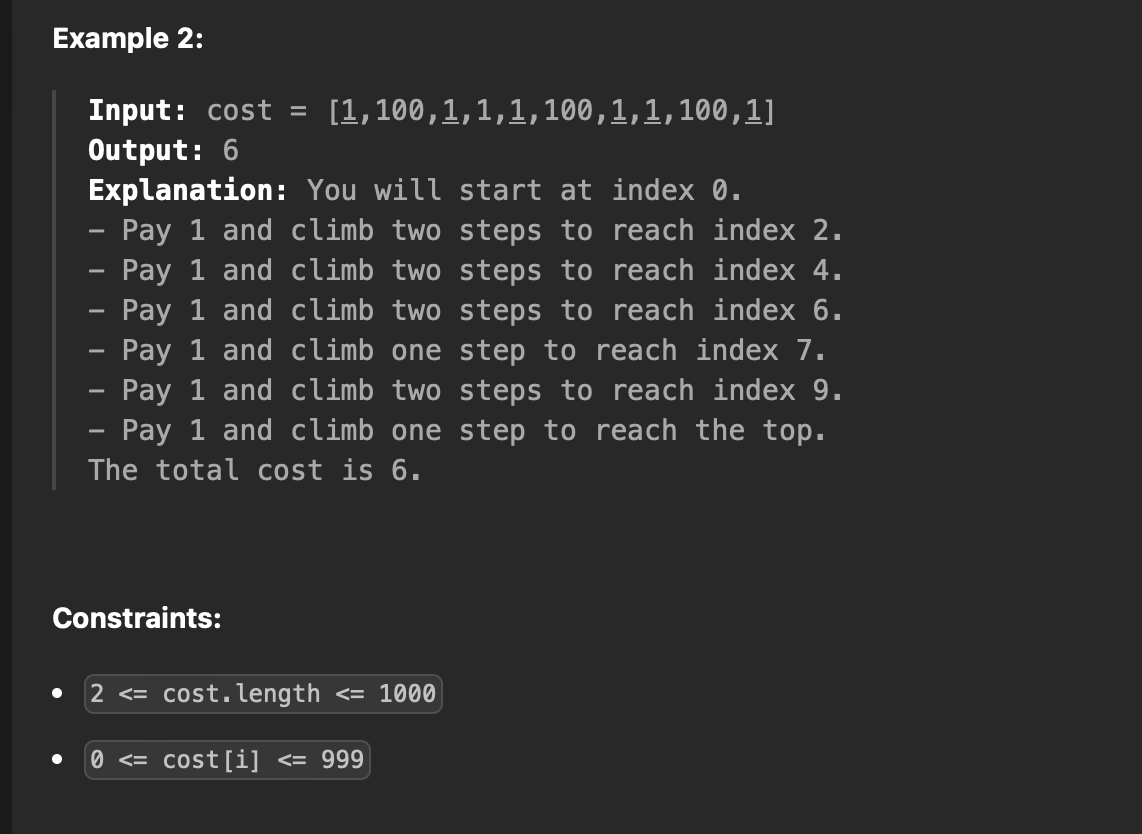
예를 들어 case 1의 cost=[10,15,20] 의 경우, 주어진 계단 3개(cost의 배열의 길이)를 모두 오른 4층이 최고점이므로, 4층까지 가기 위해서의 최소 cost를 구해야 한다.

위에서 정점으로 배열을 추가해주면 cost = [10,15,20,0] 이 되고,
최종 0에 도달하기 위해서는 최종 층에 도달하기 위해서 움직일 수 있는 경우의 수, 한 칸 전과 두 칸전의 cost를 업데이트한다.
한 칸 전의 경우인 cost[3]은 도달하기 위해서 한 번만 이동할 수 있기 때문에 cost는 20이고 그대로 업데이트하지 않고 둔다.
두 칸 전의 cost는 cost[2]인 15가 한 칸씩 움직여서 도달가능한 cost 35(15+20)과, 두칸을 한번에 이동해서 도달하는 cost 15가 있다. 여기서의 최저 비용인 15를 cost[2]에 업데이트 한다.

이렇게 계단을 올라가지않고 정점에서부터 내려가면서, cost들을 업데이트하는데, 한 칸 및 두 칸을 이동했을 때의 cost들을 더해서 mininum 한 cost를 첫 번째 칸까지 이동하면서 update 한 후에
주어진 cost 배열의 0과 1 인덱스 중에서 가장 낮은 cost의 값을 return 한다.

내 코드

 class Solution:
    def minCostClimbingStairs(self, cost: List[int]) -> int:
        cost.append(0)

        for i in range(len(cost)-3, -1, -1):
            cost[i] += min(cost[i+1], cost[i+2])
            
        return min(cost[0], cost[1])

        

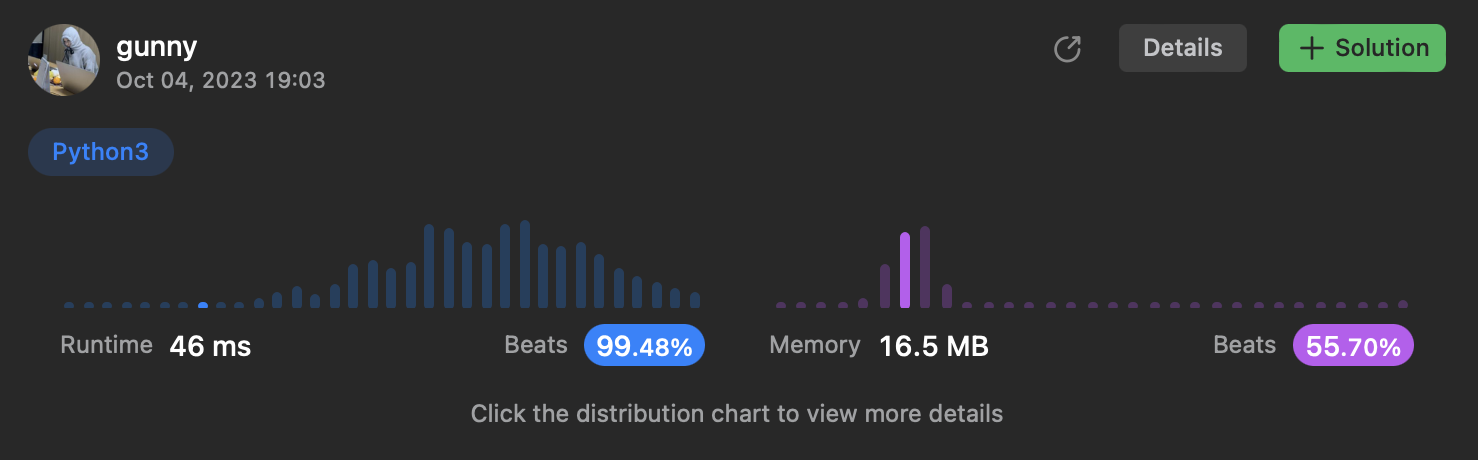
증빙

여담

완벽히 한국으로 돌아온 나 릿코드 시작 빠밤