[2024] Day18. 931. Minimum Falling Path Sum

gunny·2024년 1월 20일

931. Minimum Falling Path Sum 931. Minimum Falling Path Sum python leetcode 931. Minimum Falling Path Sum

코딩테스트

목록 보기

331/530

2024년부터 새롭게 다시 시작하는 코딩테스트

2024년 1월 18일 (목)
Leetcode daily problem

931. Minimum Falling Path Sum

https://leetcode.com/problems/minimum-falling-path-sum/description/?envType=daily-question&envId=2024-01-19

Problem

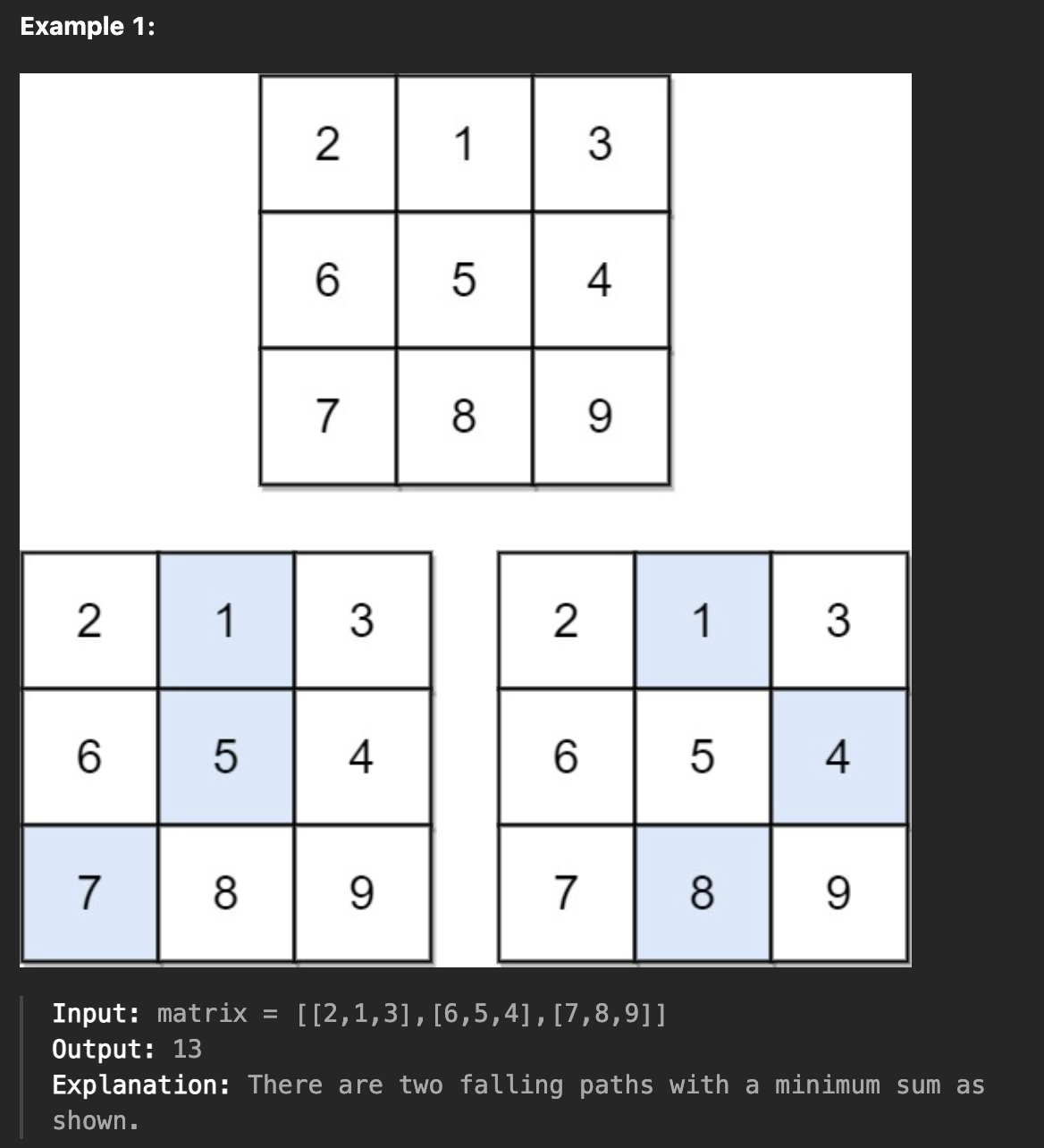
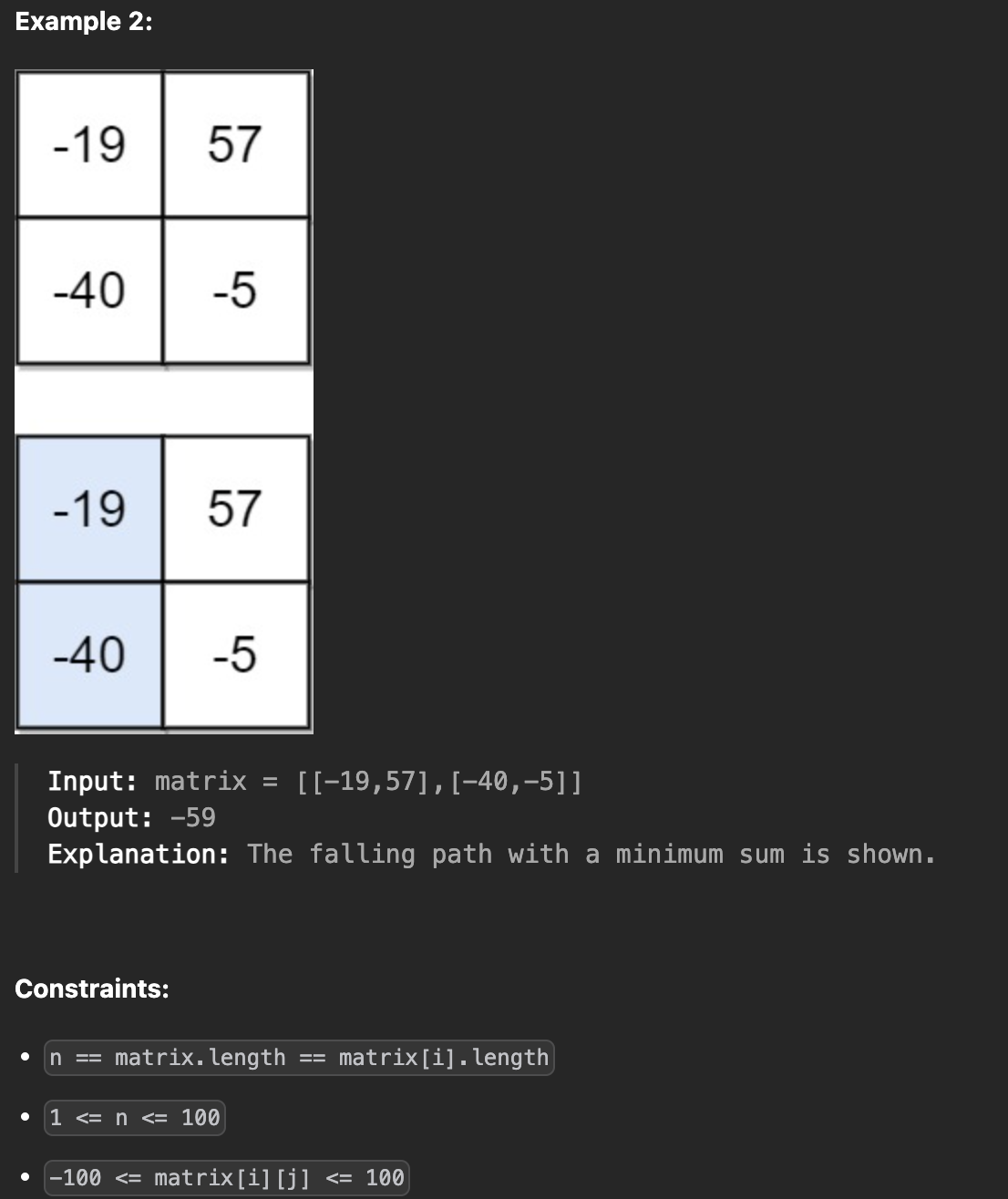
정수로 구성된 정사각형(nxn) 그리드가 있을 때,
경로가 첫 번째 행에서 마지막 행으로 이동하고, 행의 이동시 현재 좌표 기준 대각 왼쪽, 직선 아래, 대각 오른쪽으로 이동할 수 있다.
첫 번째 행의 무작위 위치에서 시작해서 아래로 내려가는 경로에서 선택된 정수 원소의 숫자을 합해 가는데, 가장 적은 합을 찾아 반환한다.

Solution

동적 프로그래밍(Dynamic Programming)

문제를 간단한 하위 문제로 나누고 하위 문제의 답을 기반으로 전체 문제의 답을 찾아나가는 Dynamic programming을 사용한다.

행렬의 각 행을 반복하면서 이전 행에 대한 최소 합계를 유지하기 위해 임시 목록을 활용한다.

한 행에서 다음 행으로 이동할 때 최소 합계 목록을 업데이트해서 행의 가능한 각 끝 위치에 대해 해당 지점까지의 최소 합계를 항상 포함하게 한다. 각 단계에서 가능한 세 가지 이동(아래, 왼쪽 아래, 오른쪽 아래)을 살펴보고 지금까지 합이 가장 작은 것을 선택한다.

여기서는 행의 각 위치에서의 최소 합계가 이전 행의 바로 위 또는 대각선 위에 있는 위치의 합계에만 의존한다는 것으로, 따라서 최소 합계를 계산하기 위해 전체 경로를 기억할 필요가 없으며 이전 행의 값만 기억하면 된다는 것이다.

행의 탐색이 끝나면 마지막 행에 대한 최소 합계가 포함되며 가장 작은 숫자는 전체 행렬에 대한 최소 합계가 된다.

Code

class Solution:
    def minFallingPathSum(self, matrix: List[List[int]]) -> int:
        ROWS, COLS = len(matrix), len(matrix[0])
        dp= matrix[0]

        for row in range(1, ROWS):
            tmp = [0] * COLS
            for col in range(COLS):
                tmp[col] = matrix[row][col] + min(dp[max(0,col-1):min(col+2,COLS)])
            dp = tmp
        return min(dp)