[2024] Day6. 1235. Maximum Profit in Job Scheduling

2024년부터 새롭게 다시 시작하는 코딩테스트

2024년 1월 6일 (토)
Leetcode daily problem

1235. Maximum Profit in Job Scheduling

https://leetcode.com/problems/maximum-profit-in-job-scheduling/?envType=daily-question&envId=2024-01-06

Problem

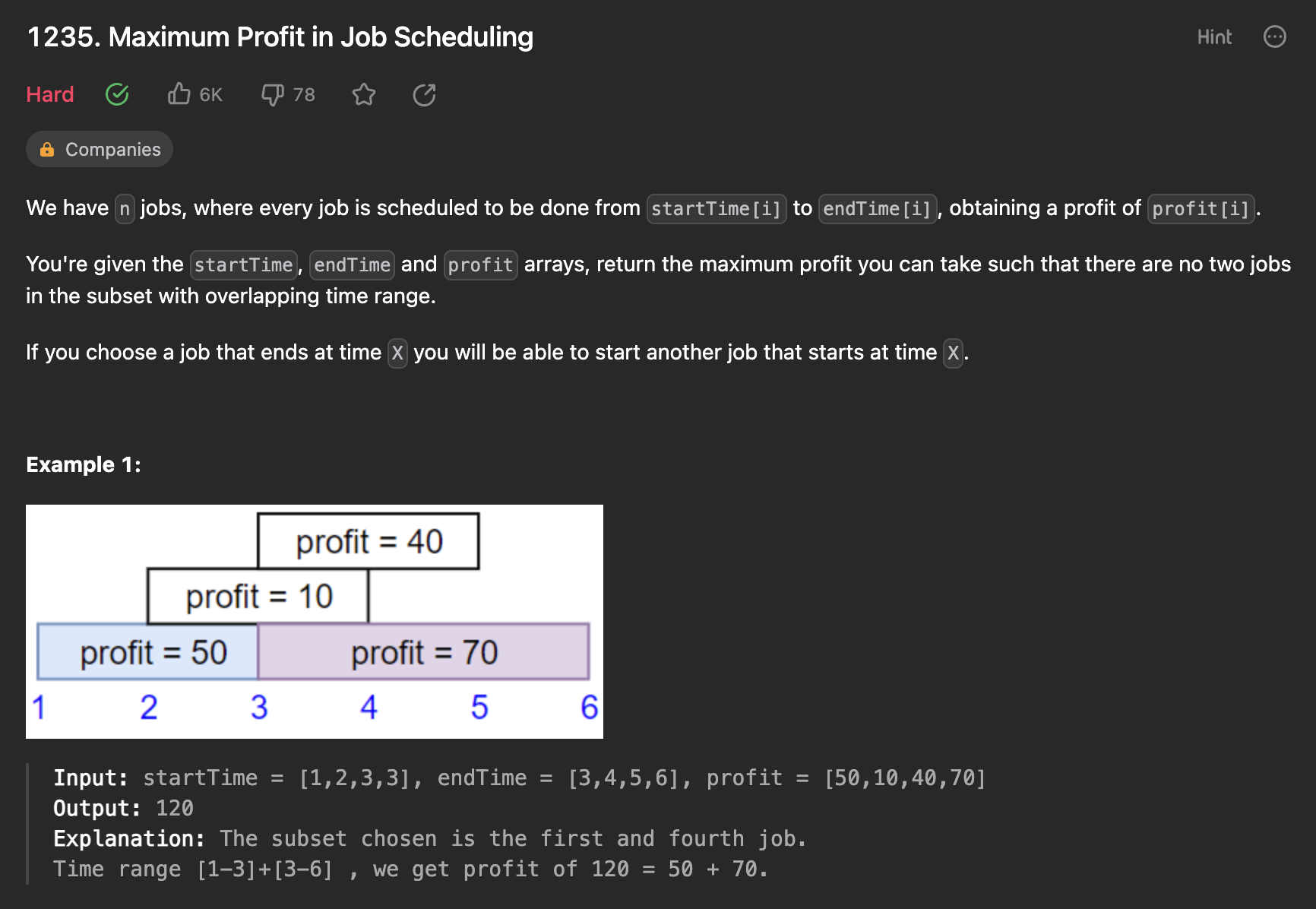
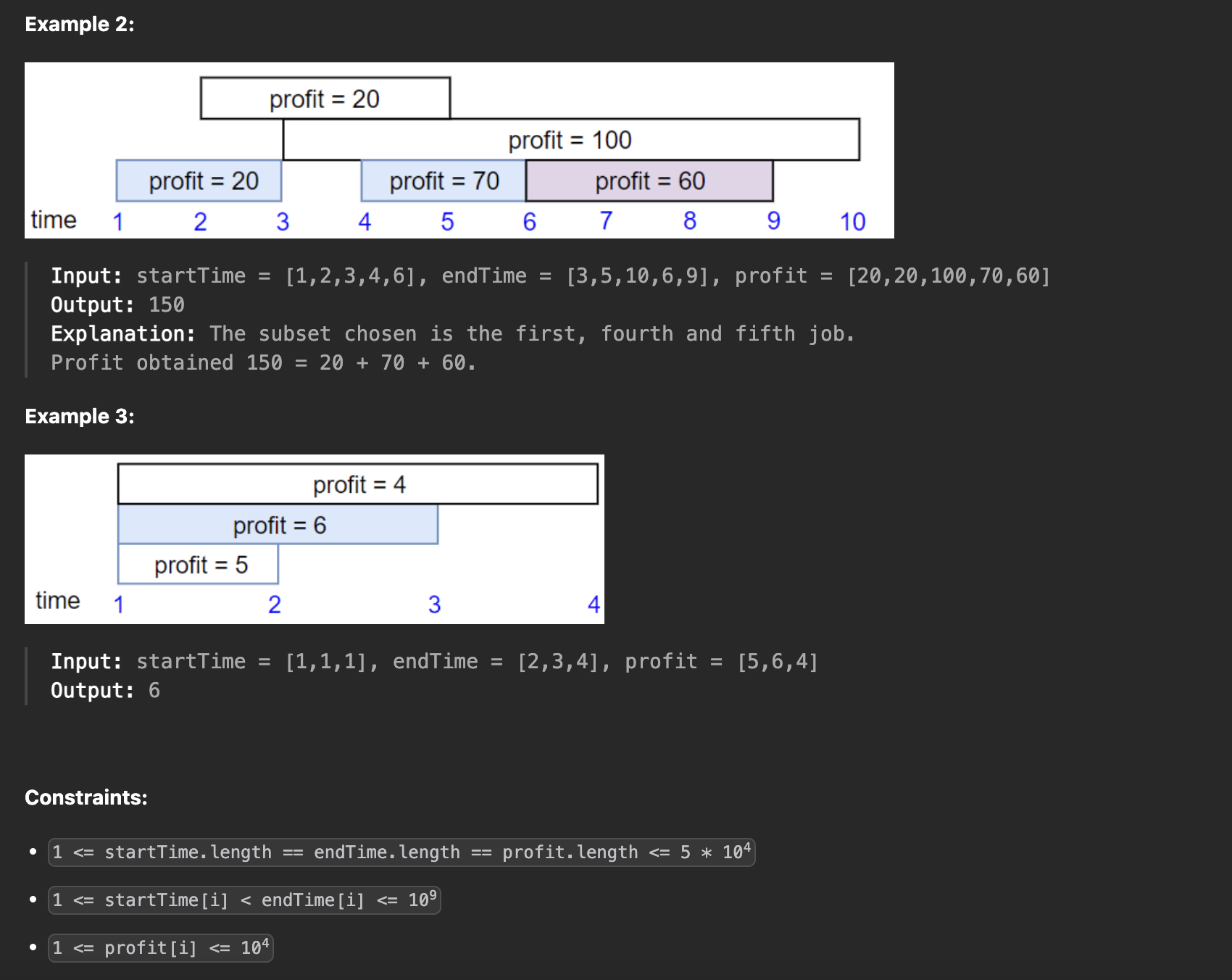
주어진 작업들을 수행하여 최대 이익을 얻는 문제이다.
각 작업은 시작 시간(startTime), 종료 시간(endTime), 이익(profit)으로 구성되어 있으며, 한 작업을 수행하면 해당 작업의 종료 시간까지의 이익이 얻어진다. 동시에 두 개 이상의 작업을 수행할 수 없고, 작업들은 서로 겹치지 않아야 한다.

Solution

Dynamic programming + binary search

Dynamic programming으로만 풀면 time limit error가 발생한다.
그래서 Dynamic programming과 binary search를 같이 이용해야한다.

(1) 먼저 작업을 종료 시간을 기준으로 오름차순 정렬한다.
(2) 동적 프로그래밍(dp)를 사용하여 최대 이익을 계산한다.
각 작업에 대해 현재 작업을 선택했을 때의 최대 이익을 계산하느넫,
현재 작업의 이전에 종료된 작업 중에서 가장 큰 이익을 갖는 작업을 찾아야한다.
(3) 이진 탐색을 통해 현재 작업의 시작 시간보다 빨리 끝나는 작업 중 가장 큰 이익을 갖는 작업을 찾는다.
(4) 현재 작업을 선택했을 때의 최대 이익을 계산하여 dp table을 갱신한다.

Code

class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        ans = [1] * len(nums)

        for i in range(len(nums)-2,-1,-1):
            for j in range(i+1, len(nums)):
                if nums[i] < nums[j]:
                    ans[i] = max(ans[i], 1+ans[j])

        return max(ans)
        

Complexicity

시간 복잡도

이중 반복문을 사용하고 있으므로 O(n^2) 이다.

공간 복잡도

배열 nums의 길이에 비례하는 O(n) 이다.

---

개선

• 위의 코드는 배열의 길이가 길어질수록 효율성이 떨어져서, 이진탐색을 통해서 개선할 수 있다.

class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        tmp = [0]*len(nums)
        size = 0

        for num in nums:
            left, right = 0, size
            while left<right:
                mid = (left+right)//2
                if tmp[mid] < num:
                    left = mid+1
                else:
                    right = mid
            
            tmp[left] = num
            if left == size:
                size +=1
        
        return size