[2024] day 104. Leetcode 42. Trapping Rain Water

2024년부터 새롭게 다시 시작하는 코딩테스트

2024년 4월 12일 (금)
Leetcode daily problem

42. Trapping Rain Water

https://leetcode.com/problems/trapping-rain-water/?envType=daily-question&envId=2024-04-12

Problem

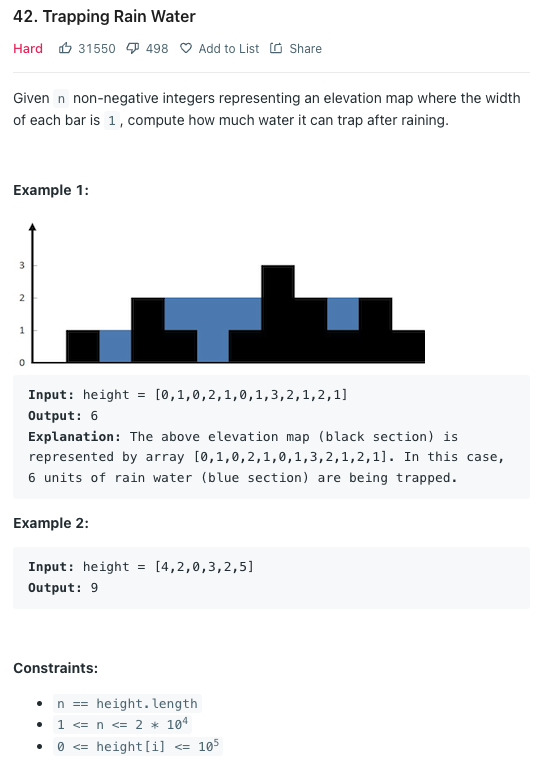
각 막대의 너비가 1인 높이를 나타내는 음이 아닌 정수 n으로 구성된 배열이 주어 질 때, 해당 배열에 얼마나 많은 물을 가둘 수 있는지 계산한다.

Solution

two pointer 혹은 stack

해당 문제는 stack을 이용해서 주어진 배열에서 각 지점의 높이를 토대로 물이 쌓일 수 있는 부분을 파악해서 해결할 수 있다.

1. 각 지점에서 왼쪽과 오른쪽으로 가장 높이를 저장하는 배열을 만든다.
2. 스택을 이용해 배열을 순회하면서 현재 높이와 스택의 top을 비교한다.
3. 만약 현재 높이가 top보다 높다면 top을 pop하고 현재 높이와 top 사이에 빗물이 채워질 수 있는 공간을 계산한다.
4. 그렇지 않으면 현재 높이를 stack에 push 한다.
5. 배열을 끝까지 반복해서 빗물이 쌓이는 부분을 계산한다.

Code

class Solution:
    def trap(self, height: List[int]) -> int:
        if not height:
            return 0
        
        stack = []
        water = 0
        
        for i in range(len(height)):
            while stack and height[i] > height[stack[-1]]:
                top = stack.pop()
                if not stack:
                    break
                
                distance = i - stack[-1] -1
                h = min(height[i], height[stack[-1]])- height[top]
                water += distance * h
                
            stack.append(i)
            
        return water

각 높이를 스택에 push하면서 현재 높이가 스택의 top보다 큰 경우, 스택에서 top을 pop하여 현재 높이와 스택의 top 사이에 빗물이 쌓일 수 있는 부분을 계산하는 방식이다.

Complexicity

시간 복잡도

배열을 한 번 순회하면서 스택을 조작하고 계산하는 과정이 있다. height 배열의 모든 요소를 한 번씩 방문하므로, 배열의 길이가 n일 때 O(n)의 시간이 소요된다. 시간 복잡도는 O(n)이다.

공간 복잡도

주어진 배열에 대해 스택을 사용하여 최악의 경우에는 배열과 동일한 길이의 스택이 필요하기 때문, 공간 복잡도는 배열의 크기에 선형적으로 증가한다.
공간 복잡도는 O(n)이다.

---

two pointer Solution

그외에 two pointer로 해결할 수 있는 방법이다.

class Solution:
    def trap(self, height: List[int]) -> int:
        if not height:
            return 0

        l,r = 0, len(height)-1
        leftmax, rightmax = height[l], height[r]
        water = 0
        while l<r:

            if leftmax < rightmax:
                l+=1
                leftmax = max(leftmax, height[l])
                water += leftmax - height[l]

            else:
                r -=1
                rightmax = max(rightmax, height[r])
                water += rightmax - height[r]

        return water