[2024] day 108. Leetcode 623. Add One Row to Tree

gunny·2024년 4월 18일

LeetCode 623. Add One Row to Tree leetcode 623. Add One Row to Tree python

2024년부터 새롭게 다시 시작하는 코딩테스트

2024년 4월 16일 (화)
Leetcode daily problem

623. Add One Row to Tree

https://leetcode.com/problems/add-one-row-to-tree/?envType=daily-question&envId=2024-04-16

Problem

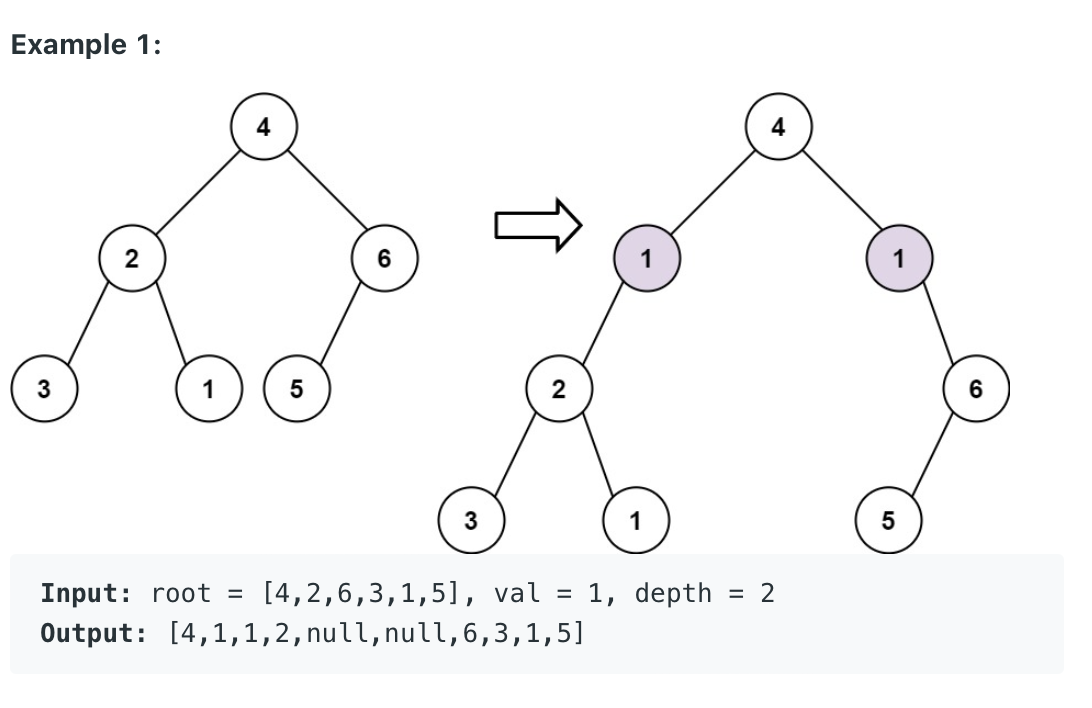
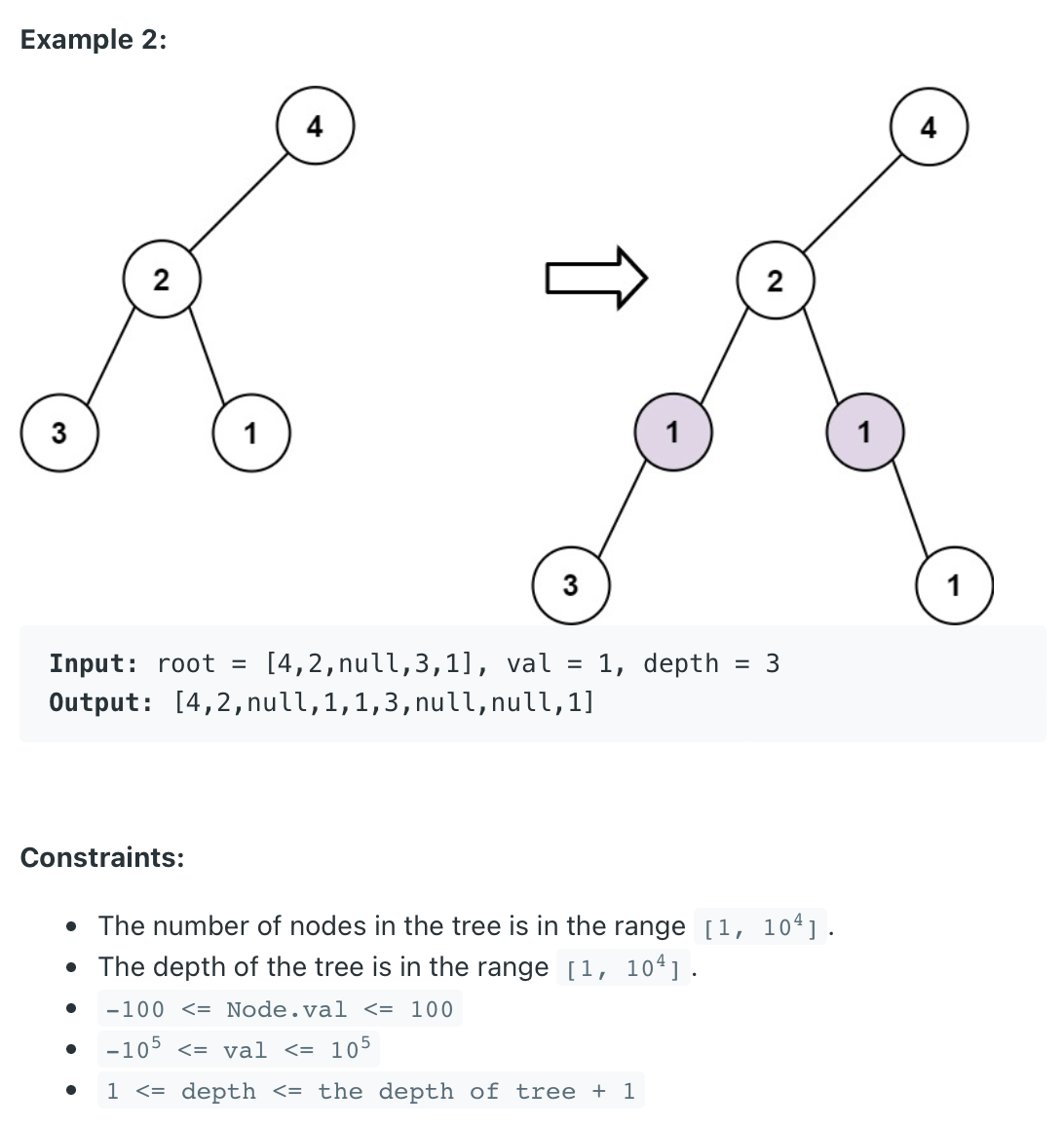
이진 트리와 두 개의 정수 val, depth가 주어지면 주어진 depth에 해당하는 이진 트리의 depth에 값이 val인 노드 행을 추가한다.
여기서 root 노드의 depth는 1이다.

추가 규칙은 다음과 같다.

정수인 depth가 주어지면 이진트리의 depth-1의 null이 아닌 각 트리 노드 cur에 대해 값 val을 cur의 왼쪽 하위 트리 루트와 오른쪽 하위 트리 루트로 사용하여 두 개의 트리 노드를 만든다.
cur의 원래 왼쪽 하위 트리는 새로운 왼쪽 하위 트리 루트의 왼쪽 하위 트리여야 합니다.
cur의 원래 오른쪽 하위 트리는 새로운 오른쪽 하위 트리 루트의 오른쪽 하위 트리여야 합니다.
깊이 == 1이면 깊이가 없음을 의미하고 즉, 전체 원래 트리의 새 루트로 val 값을 사용하여 트리 노드를 만들고 원래 트리는 새 루트의 왼쪽 하위 트리입니다.

Solution

DFS(Depth-First Search, 깊이 우선 탐색)

해당 문제는 주어진 이진 트리에 대해 특정 깊이(depth)에 새로운 노드를 추가하는 문제이다.
깊이 우선 탐색(DFS, Depth-First Search)을 통해서 트리의 각 노드를 방문하면서 목표 깊이에 도달하면 새로운 노드를 추가하고, 기존의 자식 노드를 새로운 노드의 자식으로 이동시킨다.

엣지 포인트는 주어진 depth가 1일 경우 깊이가 없음을 의미하므로 원래 트리의 새 루트로 val 값을 사용해 트리 노드를 만드는 것이다.

주어진 이진 트리를 탐색해 나갈 때 해당 트리의 깊이가 주어진 depth와 같아질 경우에는 val을 이용해 TreeNode를 만들고, 좌,우에 생성한 트리노드(new_left, new_right)를 넣은 후에 트리노드의 new_left, new_right node에 현재 루트의 left, right를 넣어준다는 것이다. 그 후에 현재 루트의 left, right를 new_left, new_right로 교체해준다.

Code

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right
class Solution:
    def addOneRow(self, root: Optional[TreeNode], val: int, depth: int) -> Optional[TreeNode]:

        if depth == 1:
            new_tree = TreeNode(val)
            new_tree.left = root
            return new_tree
        
        def dfs(node, d):
            if not node:
                return
            
            if d==depth-1:
                left_child, right_child = TreeNode(val), TreeNode(val)
                left_child.left, right_child.right = node.left, node.right
                node.left, node.right = left_child.left, right_child.right
                
            else:
                dfs(node.left, d+1)
                dfs(node.right, d+1)

        dfs(root, 1)

        return root