[2024] day 143. leetcode 78. Subsets

2024년부터 새롭게 다시 시작하는 코딩테스트

2024년 5월 21일 (화)
Leetcode daily problem

78. Subsets

https://leetcode.com/problems/subsets/?envType=daily-question&envId=2024-05-21

Problem

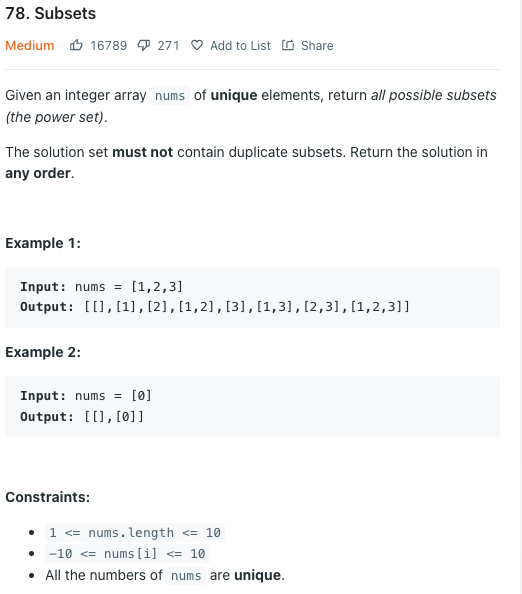
고유한 정수 요소로 구성된 배열이 주어지면 가능한 모든 하위 집합(멱집합)을 반환한다.

반환되는 하위 집합에는 중복된 하위 세트가 포함되어서는 안된다. 순서는 상관없이 하위 집합을 반환한다.

Solution

Backtracking

주어진 정수 배열의 부분집합을 구하기 위해서 비트 마스크 , 백트래킹 방법 사용이 가능한데 여기서는 백트래킹 방법을 사용했다,
재귀 함수를 이용해서 현재 인덱스의 원소를 포함하는 경우와 포함하지 않는 경우로 나누고, 현재 인덱스가 배열의 끝에 도달하면 현재 부분집합을 결과 리스트에 포함한다.
재귀 호출을 통해 모든 가능한 조합을 탐색한다.

Code

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        
        def backtracking(nums, idx, subset, subsets):
            
            if idx==len(nums):
                subsets.append(subset[:])
                return
                
            subset.append(nums[idx])
            
            backtracking(nums, idx+1, subset, subsets)
            subset.pop()
            backtracking(nums, idx+1, subset, subsets)
        
        subsets = []
        backtracking(nums, 0, [], subsets)
        
        return subsets

Complexicity

시간 복잡도

주어진 배열의 요소의 부분집합을 생성하는데 각 원소에 대해 두 가지 선택지를 가진다. (포함한다/포함하지 않는다) 따라서, 배열의 길이를 n이라고 할 때 모든 부분집합의 개수는 2^n 이다.

각 부분 집합을 만들기 위해.평균적으로 재귀호출마다 현재까지의 부분집합을 생성하고 관리하므로 O(n) 시간이 소요되어 전체 시간복잡도는 O(n*2^n)이다.

공간 복잡도

최대 재귀 호출 깊이는 배열의 길이로, 각 재귀 호출에서 새로운 재귀 호출이 생성될 때마다 하나의 함수 호출이 스택에 쌓이므로 재귀 호출 스택의 공간복잡도는 O(n) 이다. 이때 결과를 저장하는 공간에서 결과를 저장하는 subsets은 2^n 개의 부분집합을 저장하고, 각 부분집합의 평균 길이는 n/2 이다.
그래서 결과를 저장하는데 필요한 공간 복잡도는 O(n*2^n) 이다.

시간 복잡도 및 공간복잡도 모두 지수적 복잡도에 기인한다.