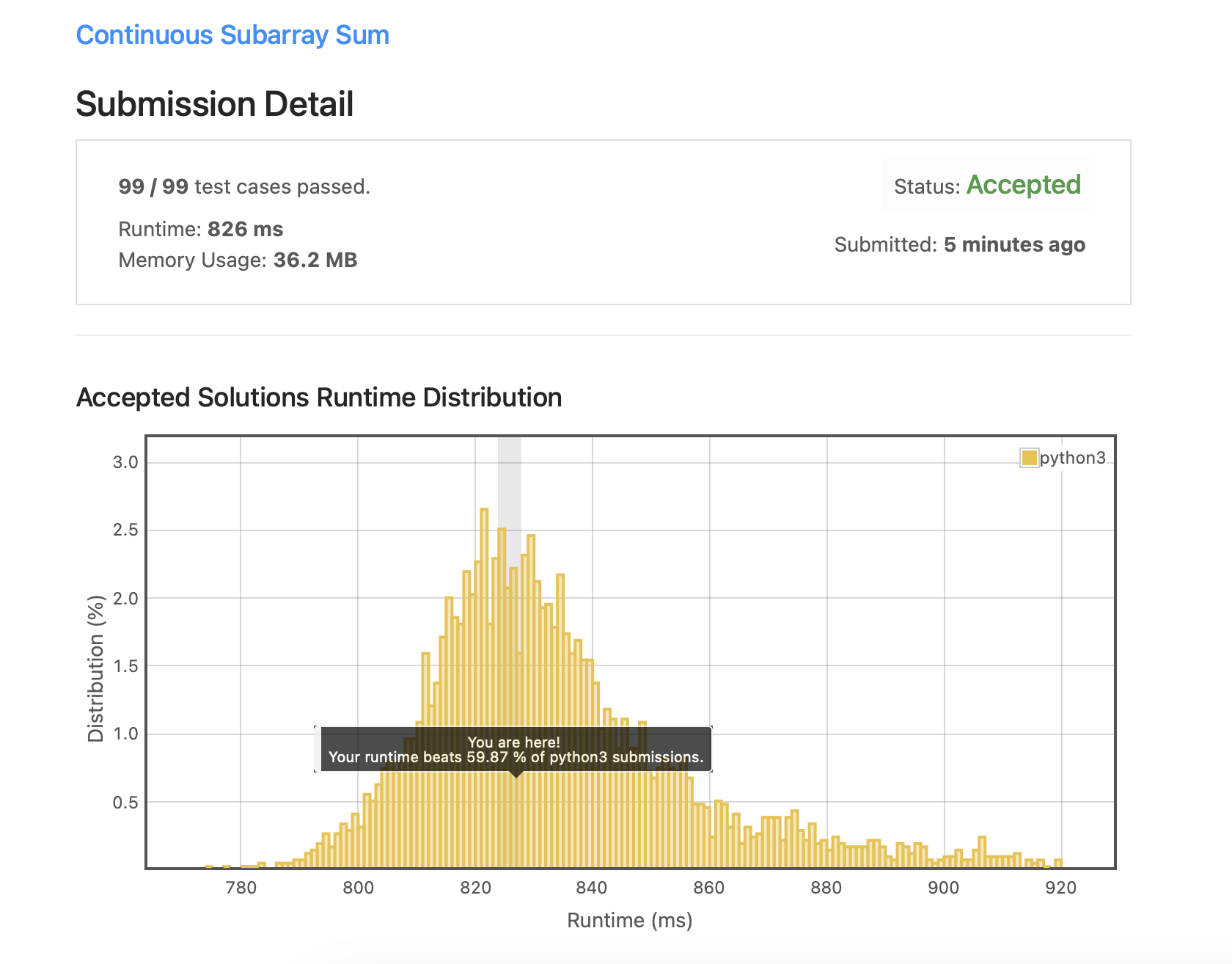
[2024] day 161. Leetcode 523. Continuous Subarray Sum

2024년부터 새롭게 다시 시작하는 코딩테스트

2024년 6월 8일 (토)
Leetcode daily problem

648. Replace Words

https://leetcode.com/problems/continuous-subarray-sum/?envType=daily-question&envId=2024-06-08

Problem

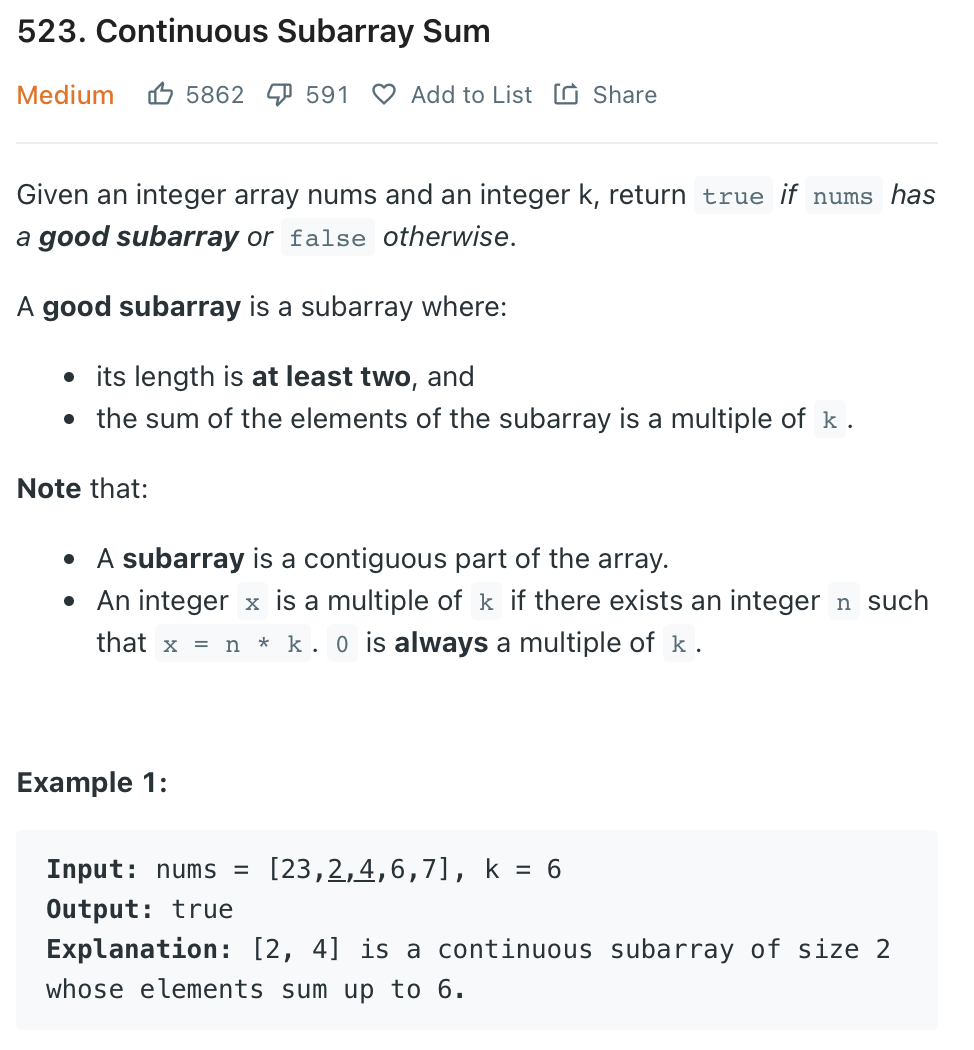
정수 배열 nums와 정수 k가 주어지면 nums에 "good subarray" 에 해당하면 True를 반환하고 그렇지 않으면 False를 반환한다.

여기서 "good subarray"는 다음과 같은 배열이다.

• 길이가 적어도 2보다 크고,
• 하위 배열 요소의 합이 k의 배수

참고 사항:

• 하위 배열은 배열의 인접한 부분(연속된 부분)
• x = n * k인 정수 n이 존재하는 경우 정수 x는 k의 배수이다.
  0은 항상 k의 배수이다.

Solution

Prefix Sum + Hashing

이 문제를 해결하기 위해서는 모듈러 연산(modular arithmetic)을 활용하여 부분 배열의 합이 k의 배수인지 확인할 수 있다.
모듈러 연산(Modular Arithmetic)은 수학에서 두 숫자를 나눈 나머지를 계산하는 연산이다.

연속 부분 배열의 합이 k의 배수인지 확인하는 문제에서 모듈러 연산을 사용할 수 있는데, 부분 합의 모듈러 값을 저장하여 같은 모듈러 값을 갖는 두 부분 배열이 있으면, 그 사이의 부분 배열의 합이 k의 배수임을 확인할 수 있다.

예를 들어, 배열 [23, 2, 6, 4, 7]가 있을 때, 각 인덱스에서의 부분 합은 다음과 같다.

부분 합 1: 23
부분 합 2: 23 + 2 = 25
부분 합 3: 23 + 2 + 6 = 31
부분 합 4: 23 + 2 + 6 + 4 = 35
부분 합 5: 23 + 2 + 6 + 4 + 7 = 42

이를 모듈러 연산 k=6 으로 나머지를 계산하면

23 mode 6 = 5
25 mod 6 = 1
31 mod 6 = 1
35 mod 6 = 5
42 mod 6 = 0

이 되고 부분 합의 나머지는 [5,1,1,5,0] 이 된다.

동일한 나머지를 갖는 두 부분의 합이 있을 때, 이 두 부분의 합 사이의 구간 합이 k의 배수임은

23 mod 6 = 5,
35 mod 6 = 5 일때

35-23 = 12로 12는 6의 배수이다.
즉 이 구간의 합은 k의 배수가 된다.

Code

class Solution:
    def checkSubarraySum(self, nums: List[int], k: int) -> bool:
        prefix_sum = 0
        sum_map = {0:-1}
        
        for i in range(len(nums)):
            prefix_sum = (prefix_sum + nums[i]) % k
            
            if prefix_sum in sum_map:
                if i - sum_map[prefix_sum] > 1:
                    return True
            else:
                sum_map[prefix_sum] = i
                
        return False

Complexicity

시간 복잡도

주어진 배열 nums 배열을 한 번 순회한다.
각 배열을 순회하면서 prefix_sum 업데이트와 prefix_sum%k와 sum_map의 조회는 상수 시간 O(1)로 이루어진다.
즉, 전체 시간 복잡도는 O(n)이다.

공간 복잡도

여기서 추가적으로 사용하는 주요 공간은 해시맵 sum_map이다.
최악의 경우, 모든 서로 다른 prefix_sum % k 값들이 해시맵에 저장될 수 있다.
그러나 해시맵의 크기는 최대 배열 nums의 길이 n에 비례한다.
즉, 해당 코드의 전체 공간 복잡도는 O(n) 이다.