[2024] day 168. Leetcode 502. IPO

2024년부터 새롭게 다시 시작하는 코딩테스트

2024년 6월 15일 (토)
Leetcode daily problem

502. IPO

https://leetcode.com/problems/ipo/?envType=daily-question&envId=2024-06-15

Problem

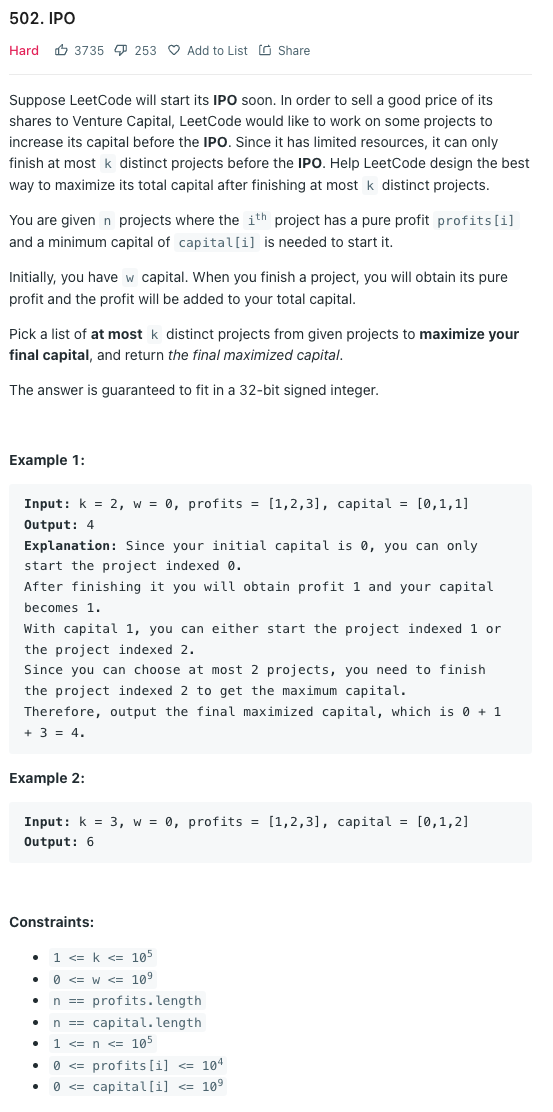
LeetCode가 곧 IPO를 시작한다고 가정한다.
LeetCode는 자사 주식을 좋은 가격에 Venture Capital에 매각하기 위해 IPO 이전에 자본금을 늘리는 일부 프로젝트를 진행하고자 한다.
자원이 제한되어 있기 때문에 IPO 이전에는 최대 k개의 개별 프로젝트만 완료할 수 있다. LeetCode가 최대 k개의 개별 프로젝트를 마친 후 총 자본을 극대화할 수 있는 최선의 방법을 설계해야 한다.

i번째 프로젝트가 profits[i]을 갖고 이를 시작하려면 capital[i]이 필요한 n개의 프로젝트가 제공된다.
처음에는 'w' 만큼의 capital이 있고, 프로젝트를 완료하면 순수한 profit을 얻게 되며 이 profit은 전체 자본(total capital)에 추가됩니다.

최종 자본을 최대화하기 위해 주어진 프로젝트에서 최대 k개의 개별 프로젝트 목록을 선택하고 최종 최대화된 자본(final capital)을 반환합니다.

답은 32비트 부호 있는 정수가 보장된다.

Solution

greedy + priority heap (그리디 + 우선순위 큐)

각 프로젝트에 필요한 capital과 profit을 합친 후에, capital을 기준으로 오름차순으로 정렬한다. 처음 주어진 'w' 만큼의 capital에 해당하는 project를 진행할 수 있기 때문이다.

그 이후 현재 capital로 실행 가능한 프로젝트들을 최대 힙에 추가하고, 최대 힙에서 가장 profit이 큰 프로젝트를 선택한다.
그 프로젝트로 얻은 profit을 현재 capital에 더하는 과정을 반복하는데 주어진 최대 'k' 개의 프로젝트를 선택하거나 더 이상 선택할 수 없는 프로젝트가 없을 때 까지 반복한다.

즉, capital 요구량을 기준으로 프로젝트를 정렬하고, 현재 자본 'w'로 시작 가능한 프로젝트를 최대 힙에 추가하면서, 최대 힙에서 가장 큰 이익을 내는 프로젝트를 선택해 해당 이익을 현재 자본에 더해간다. 최대 'k'개에 도달하거나 더 이상 선택할 프로젝트가 없으면 로직을 종료한다.

Code

class Solution:
    def findMaximizedCapital(self, k: int, w: int, profits: List[int], capital: List[int]) -> int:
        projects = list(zip(capital, profits))
        projects.sort(key=lambda x: x[0])
        
        n = len(projects)
        i = 0
        max_heap = []
        heapq.heapify(max_heap)
        
        for _ in range(k):
            while i < n and projects[i][0] <= w:
                heapq.heappush(max_heap, -projects[i][1])
                i+=1
                
            if not max_heap:
                break
            
            w += -heapq.heappop(max_heap)
            
        return w

Complexicity

시간 복잡도

해당 코드의 알고리즘은 시간복잡도가 O(n log n)이다.
주어진 프로젝트에 대해서 heapq.heappush를 사용할 때 최악의 경우 'n'번까지 호출할 수 있고 각 호출은 O(logn)의 시간이 소요된다.
heapq.heappush 또한 최대 'k'번 호출당할 수 있으므로 O(log n)의 시간이 소요된다.

즉, 정렬과 힙 연산을 통한 시간 복잡도는 O(nlogn + klogn)이다.
여기서 n은 프로젝트의 개수, k는 최대힙이 호출되는 횟수 이다.

공간 복잡도

projects의 배열을 정렬하는 과정에서 O(n)의 공간이 필요하다.
최악으로 최대 힙에서도 모든 프로젝트가 들어갈 수 있어 O(n)의 공간이 필요하다.
즉 최종 공간복잡도는 O(n) 이다.