[2024] day 178. Leetcode 1038. Binary Search Tree to Greater Sum Tree

2024년부터 새롭게 다시 시작하는 코딩테스트

2024년 6월 25일 (화)
Leetcode daily problem

1038. Binary Search Tree to Greater Sum Tree

https://leetcode.com/problems/binary-search-tree-to-greater-sum-tree/?envType=daily-question&envId=2024-06-25

Problem

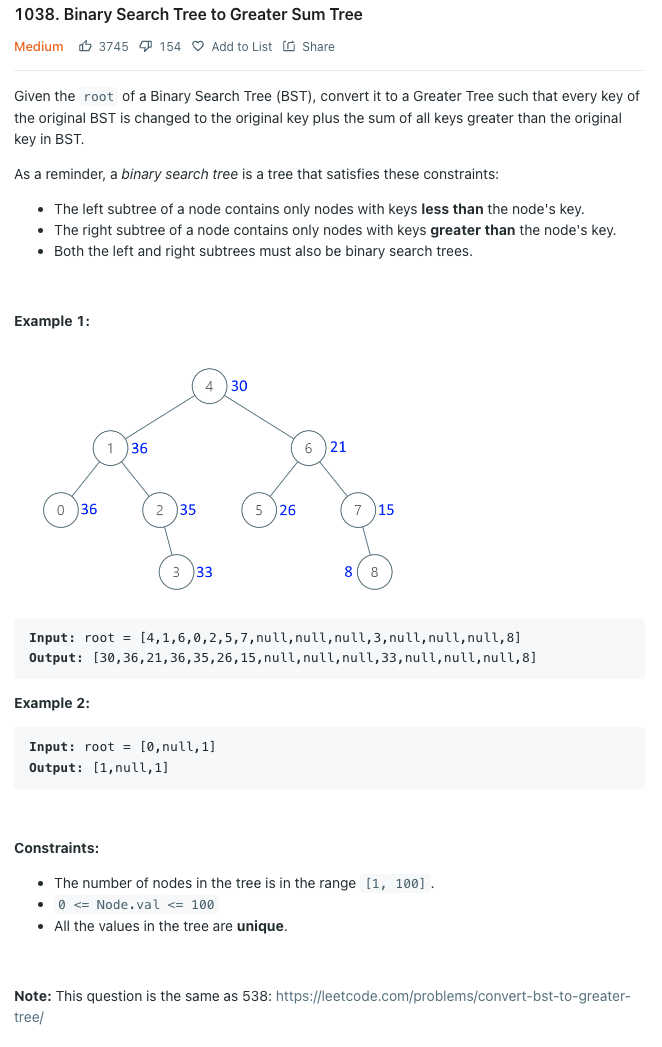
BST(이진 검색 트리)의 루트가 주어지면 "Greater Sum Tree"로 변환하는 것이다. 각 노드의 값을 원래 트리에서 그 노드보다 크거나 같은 모든 노드의 값의 합으로 바꾸는 것이다.

이진 검색 트리는 다음 제약 조건을 충족하는 트리이다.

• 노드의 왼쪽 하위 트리에는 해당 노드의 키보다 작은 키를 가진 노드이다.
• 노드의 오른쪽 하위 트리에는 노드의 키보다 큰 키를 가진 노드이다.
• 왼쪽 및 오른쪽 하위 트리도 모두 이진 검색 트리여야 함

Solution

brute force (in-order), reverse in-order, iterative reverse in-orer

[1] in-order traversal (brute-force)

제일 먼저 접근 했던 방식은 burte-force 방법으로 중위 순회(in-order) 알고리즘을 사용하는 방법이다.

이진 검색 트리에서 노드의 왼쪽 하위 트리에 있는 모든 노드는 해당 노드보다 작은 값을 가지며 오른쪽 하위 트리에 있는 모든 노드는 더 큰 값을 갖는다. 순차 순회 중에는 왼쪽 하위 트리에서 루트 노드로 이동한 다음 오른쪽 하위 트리로 이동하게 된다, 따라서 이진 검색 트리에서 순차 순회는 오름차순으로 노드 값을 생성한다.

순차 순회를 사용하여 트리를 순회하면서 모든 노드 값을 배열에 저장해서 이제 트리를 다시 탐색하고 배열에 있는 모든 더 큰 값의 합으로 원래 값을 증가시켜 각 노드의 값을 수정한다.

class Solution:
    def bstToGst(self, root: TreeNode) -> TreeNode:
        self.inorder_travel = []
        self.inorder(root)
        self.inorder_travel.reverse()
        self.replaceVal(root)
        
        return root
    
    def inorder(self, root):
        if not root:
            return
        
        self.inorder(root.left)
        self.inorder_travel.append(root.val)
        self.inorder(root.right)
        
    def replaceVal(self, root):
        if not root:
            return
        
        self.replaceVal(root.left)
        self.replaceVal(root.right)
        
        val_sum = 0
        
        for i in self.inorder_travel:
            if i > root.val:
                val_sum += i
                
            else:
                break
                
        root.val += val_sum

해당 코드는 중위 순회를 사용해서 모든 노드를 방문하고 O(n), 위의 replaceVal 함수에서 각 노드를 방문하면서 self.inorder_travel의 배열을 탐색하면서 조건에 맞는 값을 합산하는데 배열의 크기가 n이고 노드의 방문도 n번 일어나 해당 시간 복잡도가 O(n^2) 이다.
위의 self.inorder_travel을 reverse 하는데서도 O(n)이 소요된다. 즉 전체 시간복잡도는 O(n^2) 이다.
공간복잡도는 트리의 모든 노드 값을 저장하므로 O(n) 이고, inorder함수와 replaceVal 함수 모두 재귀 호출을 사용하고, 해당 재귀 호출 시 트리의 깊이 만큼 재귀 호출 스택을 사용해 트리의 깊이에 따라 공간이 필요하여 전체 공간 복잡도는 O(n) 이다.

이 방법을 최적화 하기 위해서 reverse in-order traversal 을 사용한다.

[2] reverse in-order traversal

여기서는 오른쪽 서브트리를 먼저 순회하는 방법을 사용해서 큰 값부터 닥은 값 순서대로 노드를 방문한다.
재귀를 이용해 오른쪽 서브 트리르 먼저 방문하는데 이렇게 되면 가장 큰 값을 가진 오른쪽 끝 노드에 도달할 수 있다.
트리를 순회하면서 각 노드의 값을 현재까지 방문한 노드의 값들로 업데이트하여 큰 값에서 작은 값 순서로 노드를 방문하면서 합계를 점진적으로 업데이트 한다.
오른쪽 서브트리를 모두 방문하면 왼쪽 서브트리로 이동해 동일한 과정을 반복하면 된다. 즉 오른쪽->루트->왼쪽 순으로 방문하고, 방문 순서는 가장 큰 값-> 다음 큰 값 -> 가장 작은 값 등이 된다.
이 과정에서 모든 노드를 내림차순으로 방문해서, 각 노드의 값을 이전에 방문했던 모든 노드의 값들의 합으로 업데이트 할 수 있다.

class Solution:
    def bstToGst(self, root: TreeNode) -> TreeNode:
        node_sum = [0]
        self.getSum(root, node_sum)
        return root
        
        
    def getSum(self, root, node_sum):
        if not root:
            return
        
        self.getSum(root.right, node_sum)
        node_sum[0] += root.val
        root.val = node_sum[0]
        self.getSum(root.left, node_sum)

재귀 호출을 통해서 각 노드의 상수 시간 연산을 수행하므로 전체 시간 복잡도는 트리의 노드 수인 O(n) 이 소요된다.
즉, 전체 시간복잡도는 O(n)이다.
공간 복잡도로는 재귀 호출이 트리의 높이 만큼 쌓이므로, 최악의 경우 편향된 트리가 되어 O(n)이 될 수 있다. node_sum의 경우 크기가 1이므로 상수 공간 O(1)을 차지하므로 전체 공간 복잡도는 O(n)이다.

[3] Iterative Reverse in-order traversal

재귀 호출로 중위 탐색을 하는 것이 아니라 stack 을 사용해 반복적인 중위 탐색을 수행하는 것이다. 트리의 노드를 순회하면서 오른쪽 끝 노드에 도달할 때 까지 스택에 노드를 추가하고, 노드를 방문할 때 마다 누적 합계를 유지한다. 현재 노드의 값을 누적 합계로 업데이트하고 왼쪽 서브트리로 이동하는 것이다.

class Solution:
    def bstToGst(self, root: TreeNode) -> TreeNode:
        node_sum = 0
        stack = []
        node = root
        
        while stack or node:
            while node:
                stack.append(node)
                node = node.right
                
            node = stack.pop()
            
            node_sum += node.val
            node.val = node_sum
            
            node = node.left
            
        return root

외부 루프는 스택이 비어있지 않거나 node가 null 이 아닐 때까지 아래의 과정을 반복하기 때문에 트리의 모든 노드를 반복하므로 트리의 노드 수인 n과 관련이 있다.
내부 루프는 node가 null이 될 때 까지 실행되고, 노드의 오른쪽 자식으로 이동하면서 스택에 노드를 추가하는 O(n)이 소요된다.
스택에서 노드를 팝하고 노드의 값을 업데이트 하는 것도 노드 당 한 번씩 발생한다. stack의 pop과 값 업데이느는 상수 시간이 소요된다.
즉, 전체 시간 복잡도는 O() 이다.

현재 스택이 경로에 있는 모든 노드를 저장하므로 스택에 최대 n개의 노드가 저장될 수 있다. 나머지는 상수 공간을 차지해 전체 공간복잡도는 O(n) 이 소요된다.

Code

하나의 문제를 풀기 위해서 3가지 접근법을 사용했고,
brute force 외에 시간 및 공간 복잡도를 O(n)으로 풀 수 있고 가장 와닿았던 풀이이다.

class Solution:
    def bstToGst(self, root: TreeNode) -> TreeNode:
        stack = []
        node_sum = 0
        node = root
        
        while stack or node:
            while node:
                stack.append(node)
                node = node.right
                
            node = stack.pop()
            node_sum += node.val
            node.val = node_sum
            
            node = node.left
            
        return root

Complexicity

시간 복잡도

외부 while 루프에서 스택이 비어 있지 않거나 노드가 null 이 아닐 때 까지이므로 트리의 모든 노드를 탐색하므로 트리의 노드의 수 n 만큼 실행된다. 내부 루프는 node가 null이 될 때 까지이며 노드의 오른쪽 자식으로 이동하면서 스택에 노드를 추가하므로 각 노드가 한 번씩 스택에 추가되 해당 루프도 n번 실행된다.
스택에서 pop하고 노드의 값을 업데이트 하는데는 상수 시간 O(1)이 소요되므로 전체 시간 복잡도는 O(n)이 소요된다.

공간 복잡도

스택에 현재 경로에 있는 모든 노드를 저장하므로, 최악의 경우에는 편향된 트리로 최대 n개의 노드가 저장될 수 있으므로 공간 복잡도는 O(n)이다.