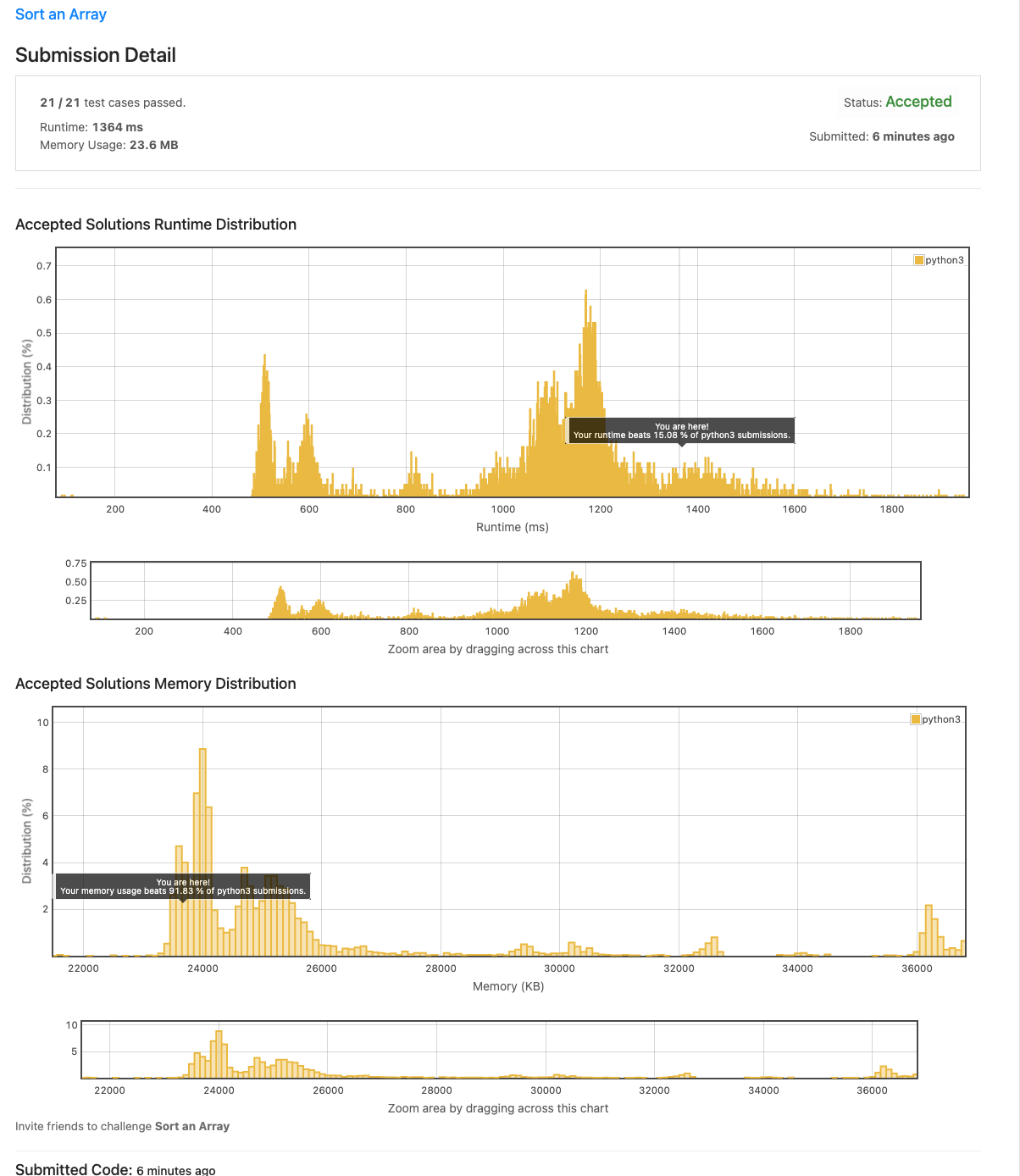
[2024] day 205. 912. Sort an Array

2024년부터 새롭게 다시 시작하는 코딩테스트

2024년 7월 25일 (목)
Leetcode daily problem

912. Sort an Array

https://leetcode.com/problems/sort-an-array/?envType=daily-question&envId=2024-07-25

Problem

주어진 정수 배열을 오름차순으로 정렬하는 문제로, 빌트인 정렬 함수를 사용하지 않고 시간복잡도 𝑂(𝑛log𝑛)를 유지하고 가능한 작은 공간 복잡성을 유지해야 한다.

Solution

Heap Sort

주어진 배열을 정렬하기 위해서는 다양한 정렬 알고리즘을 사용할 수 있는데, 몇 가지 일반적인 정렬 알고리즘을 살펴보면

[1] 퀵 정렬(Quick Sort)

• 분할 정복 알고리즘, 배열을 pivot 기준으로 두 부분으로 나누고 재귀적으로 정렬
• 평균 시간 복잡도 O(nlogn)
  최악의 시간복잡도 O(n^2) : 이미 정렬된 배열
• 공간 복잡도 O(logn) : 재귀호출로 인한 스택 공간

[2] 병합 정렬(Merge Sort)

• 분할 정복 알고리즘, 배열을 반으로 나눈 뒤 각각 정렬하고 합침
• 시간 복잡도 O(nlogn)
• 공간 복잡도 O(n) : 임시 배열 사용

[3] Heap 정렬(heap sort)

• 힙 자료 구조 기반으로 하고, 배열을 힙으로 구성해 가장 큰 값을 하나씩 추출해서 정렬
• 시간복잡도 O(nlogn)
• 공간 복잡도 O(1)

[4] 버블 정렬(Buble Sort)

• 인접한 두 원소를 비교해서 작은 것을 앞으로 보내는 방식으로 정렬, 여러번의 패스를 통해 정렬
• 시간 복잡도 O(n^2)
• 공간 복잡도 O(1)

[5] 삽입 정렬(Insertion Sort)

• 정렬된 부분과 정렬되지 않은 부분으로 배열을 나누고 정렬되지 않ㅇ느 부분의 원소를 하나씩 정렬된 부분에 삽입
• 시간 복잡도 O(n^2)
  이미 정렬된 경우 O(n)
• 공간 복잡도 O(1)

[6] 선택 정렬(Selection Sort)

• 배열을 순회하면서 가장 작은(또는 가장 큰) 원소를 선택해 정렬의 부분의 끝에 배치
• 시간 복잡도 O(n^2)
• 공간 복잡도 O(1)

: 시간 복잡도가 built-in 함수를 사용하지 않아도 O(nlogn)이면서 공간 복잡도를 O(1)으로 쓰는 힙정렬을 사용해본다.

Code

class Solution:
    def sortArray(self, nums: List[int]) -> List[int]:
        def heapify(arr, n, i):
            largest = i
            left = 2*i+1
            right = 2*i+2
            
            if left < n and arr[largest] < arr[left]:
                largest = left
                
            if right < n and arr[largest] < arr[right]:
                largest = right
                
            if largest != i:
                arr[i], arr[largest] = arr[largest], arr[i]
                heapify(arr, n, largest)

        def heap_sort(arr):
            n = len(arr)

            for i in range(n // 2 - 1, -1, -1):
                heapify(arr, n, i)

            for i in range(n - 1, 0, -1):
                arr[i], arr[0] = arr[0], arr[i]
                heapify(arr, i, 0)

    
        heap_sort(nums)
        return nums

Complexicity

시간 복잡도

시간복잡도는 O(nlogn)

공간 복잡도

공간복잡도는 O(1) 이다.