[2024] day 51. Leetcode 231. Power of Two

2024년부터 새롭게 다시 시작하는 코딩테스트

2024년 2월 19일 (월)
Leetcode daily problem

231. Power of Two

https://leetcode.com/problems/power-of-two/description/

Problem

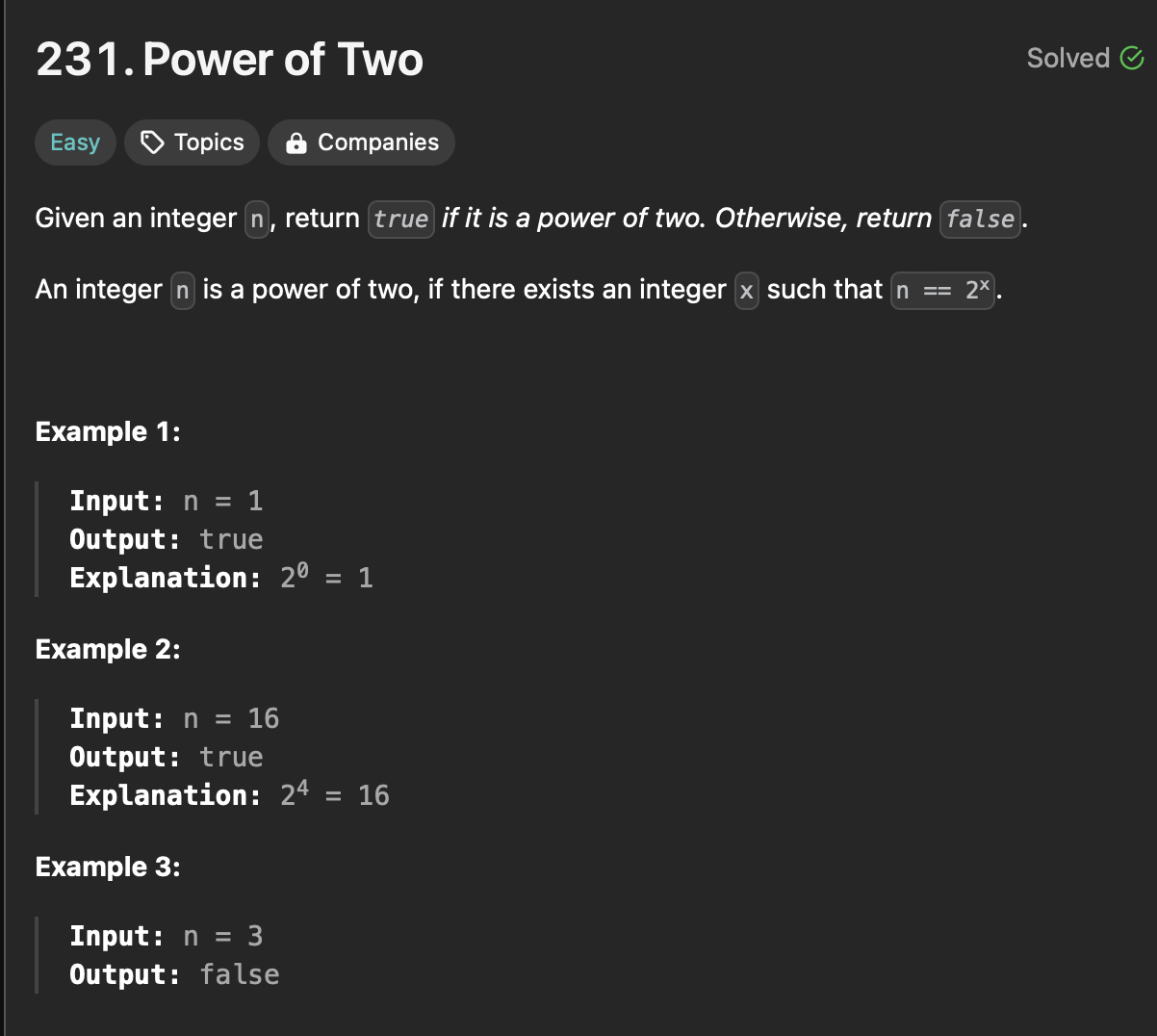
정수 n이 주어질 때 2의 거듭제곱이면 true를 반환하고, 그렇지 않으면 false를 반환한다.

n == 2x인 정수 x가 존재하는 경우 정수 n은 2의 거듭제곱이다.

Solution

AND bit 연산

주어진 n의 값이 0이라면 false, 1이라면 2^0 이므로 true를 반환하는 엣지케이스를 따로 구현하고,
그 후에 2의 거듭제곱을 업데이트해나가는 변수 two_pow를 처음에 2로 할당한 후에 n이 two_pow보다 클 동안 tow_pow에 2를 계속 곱해 나간다.
n만큼 2의 거듭제곱의 값이 업데이트 됐으면 정수 n이 거듭제곱이려면 two_pow와 같아야 하므로 해당 값이 같으면 True, 아니면 False를 반환한다.

Code

class Solution:
    def isPowerOfTwo(self, n: int) -> bool:
        if n==0:
            return False
        if n==1:
            return True
        
        two_pow = 2
        while n > two_pow:
            two_pow *=2

        return n == two_pow
        

Complexicity

시간 복잡도

two_pow 값을 n보다 크거나 같을 때까지 계속해서 두 배씩 증가시킨다. 최종 시간 복잡도는 O(log n)이다.

공간 복잡도

상수값만 계속 업데이트 하므로 최종 공간 복잡도는 O(1)이다.

---

아래에 without loops/recursion 라고 되어있어서
재귀 혹은 루프를 돌지 않고 푸는 방법이 있는데 그것은 바로 비트 연산자이다. 2진수에서 2로 나눠지는 숫자들은 맨 왼쪽 숫자빼고 모두 0으로 구성되어 있다.
2 (이진으로는 10)
4 (이진으로는 100)
8 (이진으로는 1000)
16 (이진으로는 10000)

2의 거듭제곱에서 1을 뺄 경우, 세트된 비트 이후의 모든 비트는 1이 되고, 해당 비트는 0이 된다.

2 - 1 = 1 (이진으로는 01)
4 - 1 = 3 (이진으로는 011)
8 - 1 = 7 (이진으로는 0111)
16 - 1 = 15 (이진으로는 01111)

만약 n이 2의 거듭제곱이라면, 한 개의 비트만 세트되어 있고, n - 1은 세트된 비트 이후의 모든 비트가 뒤집혀지게 된다.
n과 n - 1 사이의 비트 AND 연산을 수행하면 0이 나오게 되는데, 이는 n이 2의 거듭제곱이라는 것을 나타낼 수 있다.

즉 비트 연산으로 수행하면 시간복잡도 O(1), 공간복잡도 O(1)로 해결할 수 있다.

class Solution:
    def isPowerOfTwo(self, n: int) -> bool:
        if n==0:
            return False
        if n==1:
            return True
        
        two_pow = 2
        while n > two_pow:
            two_pow *=2

        return n == two_pow