[2024] day 59. Leetcode 543. Diameter of Binary Tree

2024년부터 새롭게 다시 시작하는 코딩테스트

2024년 2월 27일 (화)
Leetcode daily problem

543. Diameter of Binary Tree

https://leetcode.com/problems/diameter-of-binary-tree/

Problem

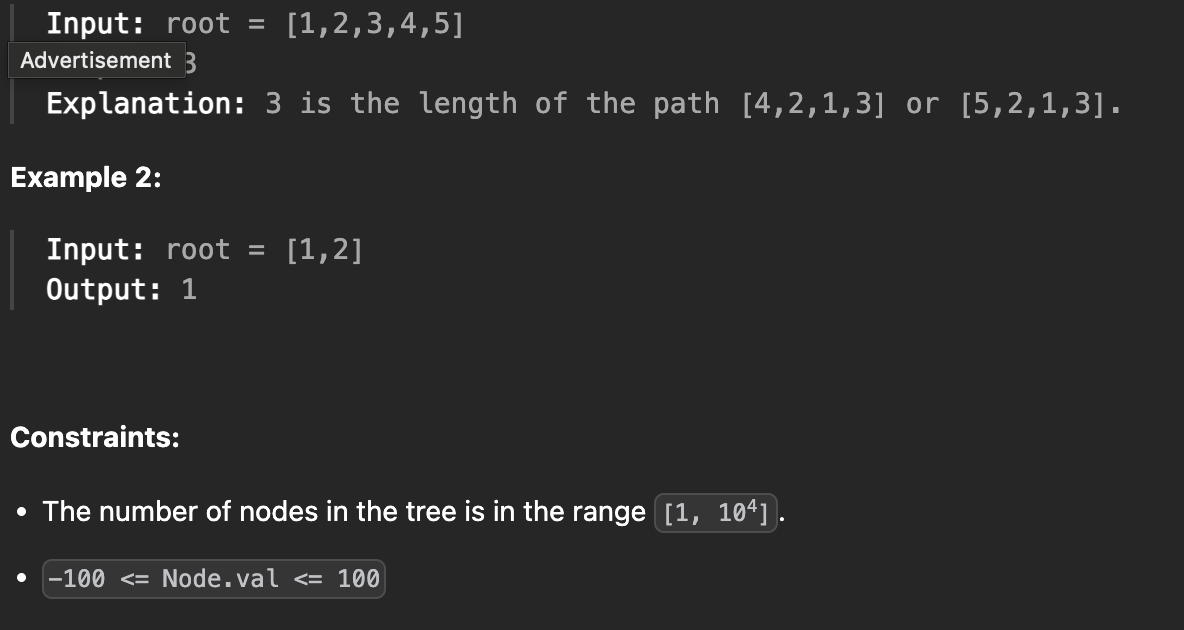
이진 트리의 루트가 주어지면 트리 지름의 길이를 반환한다.
이진 트리의 지름은 트리의 두 노드 사이에서 가장 긴 경로의 길이이다. 두 노드 사이의 경로 길이는 두 노드 사이의 간선 수로 표시된다.

Solution

Tree

주어진 트리의 터미널 노드. 즉 left node 까지의 깊이(높이)를 구하는 문제이다. 이진트리의 왼쪽, 오른쪽 노드의 각 터미널 노드까지 훑어서 최대값을 업데이트하면서 루트노드로 다시 돌아온다.
이때, 최대값을 업데이트 할 공간을 따로 만들어 줘야 한다.
업데이트할 공간을 가변 객체(mutable object)인 리스트로 하나 생성한 후 트리를 탐색하면서 깊이(직경)을 업데이트 해 간다.

Code

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def diameterOfBinaryTree(self, root: Optional[TreeNode]) -> int:
        ans = [0]
        def dfs(node):
            if not node:
                return 0
            
            left, right = dfs(node.left), dfs(node.right)
            ans[0] = max(ans[0], left+right)
            return 1+max(left,right)

        dfs(root)
        return ans[0]
       

Complexicity

시간 복잡도

해당 코드의 시간 복잡도는 주어진 트리를 다 순회하는 깊이 우선 탐색(DFS) 알고리즘으로, 이진 트리의 모든 노드를 방문하는데는 O(n)의 시간이 소요된다.
따라서 전체 시간 복잡도는 O(n) 이다.
n은 이진 트리의 노드 수입

공간 복잡도

깊이 우선 탐색(DFS) 알고리즘이 재귀적으로 구현되고,
재귀 호출 스택은 트리의 높이만큼의 메모리가 필요하다.
이진 트리의 최대 높이가 n일 수 있으므로 공간 복잡도는 O(n) 이다.
이진 트리의 직경을 담는 리스트는 상수 공간을 차지한다.
따라서 최종 공간복잡도는 O(n) 이다.