[2024] day 64. Leetcode 19. Remove Nth Node From End of List

2024년부터 새롭게 다시 시작하는 코딩테스트

2024년 3월 3일 (일)
Leetcode daily problem

19. Remove Nth Node From End of List

https://leetcode.com/problems/remove-nth-node-from-end-of-list/description/?envType=daily-question&envId=2024-03-03

Problem

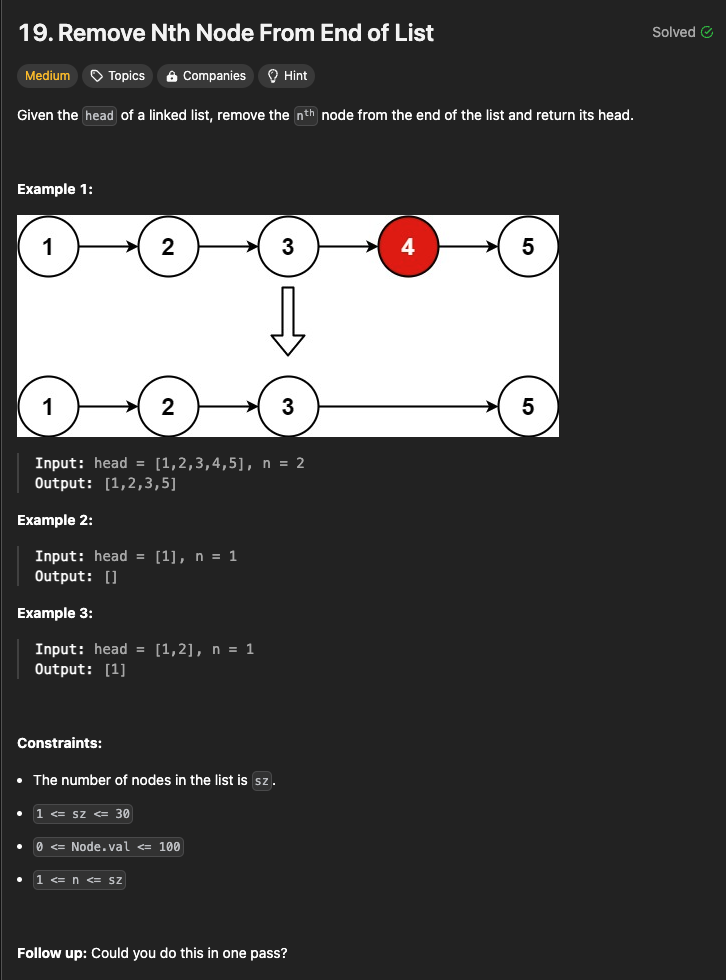
링크드 리스트(연결형 리스트)와 n이 주어질 때, 연결형 리스트의 끝에서 n번째 노드를 제거한 링크드 리스트(연결형 리스트)를 반환한다.

Solution

연결리스트, linked list

여기서는 두개의 포인터를 사용해서, 연결형 리스트를 순회하고 하나는 연결형 리스트의 끝에서 n번째 노드를 찾는데 사용한다.

먼저, dummy 노드를 생성하고 첫번째 val을 0으로 next에 주어진 head로 구성된 노드를 최적화한다.

첫 번째 포인터를 n번 만큼 이동시키고, 그런 다음 첫 번째 포인터와 두 번째 포인터를 함께 이동시킵니다. 첫 번째 포인터가 끝에 도달하면, 두 번째 포인터는 끝에서 n번째 노드의 이전 노드를 가리키게 됩니다.
노드 제거: 두 번째 포인터가 가리키는 노드의 다음 노드를 건너뛰어 해당 노드를 제거합니다.
더미 노드 반환: 더미(dummy) 노드의 다음 노드를 반환합니다.

Code

# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def removeNthFromEnd(self, head: Optional[ListNode], n: int) -> Optional[ListNode]:

        dummy = ListNode(0, head)
        slow = dummy
        fast = head

        while n>0 and fast:
            n-=1
            fast = fast.next
           
        
        while fast:
            slow = slow.next
            fast = fast.next

        slow.next = slow.next.next

        return dummy.next

Complexicity

시간 복잡도

fast 포인터를 리스트의 끝까지 이동시키는데 리스트의 크기에 비례하므로, 리스트의 길이가 n이면 시간 복잡도는 O(n) 이다.
다음 반복문에서 slow와 fast 포인터가 함께 리스트를 탐색하는데, 이 루프는 최악의 경우 fast 포인터가 리스트의 끝까지 이동하며, 이는 최대 n번 까지 걸릴 수 있어, 시간 복잡도도 O(m)이다.
즉 최종 시간복잡도는 O(m)이다.

공간 복잡도

공간 복잡도는 주어진 head 리스트 노드를 copy 하므로 O(n) 이고, 주어진 입력 링크드 리스트의 노드를 수정하면서 조작하므로 dummy, slow, fast 포인터 모두 상수 개의 포인터이므로 공간 복잡도는 O(n)이다.

[최적화]

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def removeNthFromEnd(self, head: Optional[ListNode], n: int) -> Optional[ListNode]:
        if not head:
            return None
        
        cur = head
        l = 0

        while cur:
            l +=1
            cur = cur.next

        if l == n:
            return head.next

        cur = head
        for i in range(l-n-1):
            cur = cur.next

        cur.next = cur.next.next
        return head

위의 공간 복잡도를 O(1)로 최적화 해서 푸는 방법이 존재하는데,

먼저 주어진 링크드 리스트(연결 리스트)의 길이를 구한다.
링크드 리스트를 처음부터 끝까지 순환하면서 길이를 업데이트 하고, 엣지케이스인 리스트의 길이가 0일 때 None을 리턴, 리스트의 길이가 주어진 n과 같을 때는 현재 head node의 next 값을 리턴해준다.

그 후에 주어진 길이에서 n을 빼준 값만큼 이동하면 해당 노드인데, 인덱스는 0부터 시작하므로 여기서 -1을 더 빼준 만큼만 이동한다. 그리고 나서 해당 노드의 인덱스에서 next를 한 칸 더 이동한 노드로 옮겨주면 된다.

그러면 해당 시간복잡도는 O(n), 공간복잡도는 O(1)로 풀이가 가능하다.