[2024] day 68. Leetcode 876. Middle of the Linked List

2024년부터 새롭게 다시 시작하는 코딩테스트

2024년 3월 7일 (목)
Leetcode daily problem

876. Middle of the Linked List

https://leetcode.com/problems/middle-of-the-linked-list/description/

Problem

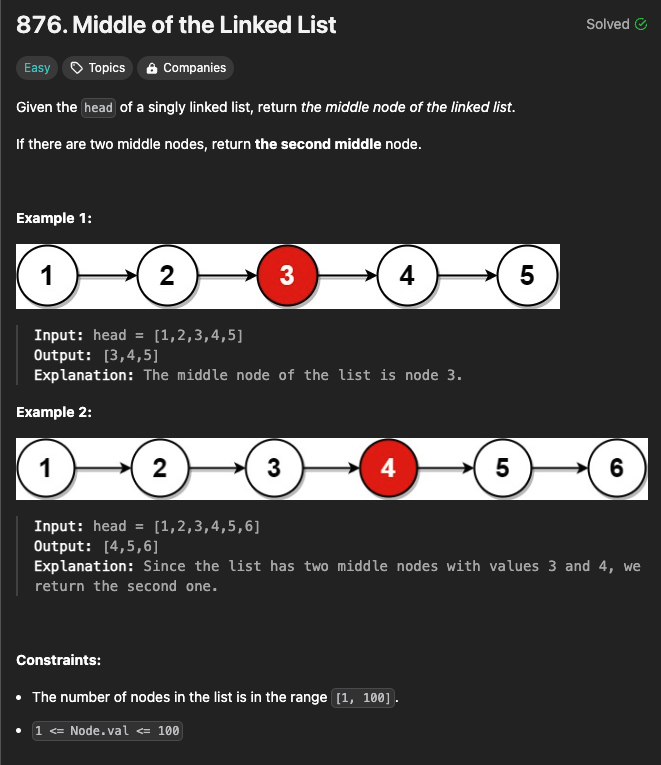
단방향 linked list가 주어질 때 해당 링크드 리스트의 중간 지점부터의 링크드 리스트를 반환한다.
만약 2개가 중간 노드이면 가장 작은 노드를 중간 지점이라고 생각한다.

Solution

linked list, two pointer

주어진 단방향 연결 리스트의 중간값을 알기 위해서
먼저 연결 리스트를 한번 탐색하면서 길이를 파악하고,
해당 길이를 2로 나누어 중간 노드의 노드 위치를 얻는다.

얻은 중간 노드 위치까지 헤드를 움직여서 해당 노드를 반환한다.

Code

class Solution:
    def hasCycle(self, head: Optional[ListNode]) -> bool:
        
        slow, fast = head, head

        while fast and fast.next:
            slow = slow.next
            fast = fast.next.next

            if slow==fast:
                return True
        
        return False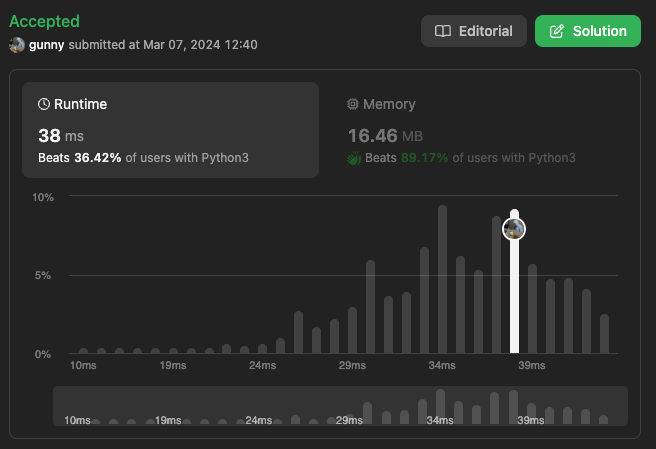

Complexicity

시간 복잡도

연결형 리스트의 모든 노드를 한 번씩 탐색하므로 시간 복잡도는 O(n)이 된다. 중간에 중간 까지 한 번 더 탐색하는 가정은 O(n/2)이고 전체적인 시간 복잡도는 O(n)이다.

공간 복잡도

포인터로만 이동하기 때문에 다른 메모리를 차지 하지 않아 공간 복잡도는 O(1) 이다.

---

# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def middleNode(self, head: Optional[ListNode]) -> Optional[ListNode]:
        slow, fast = head, head

        while fast and fast.next:
            slow = slow.next
            fast = fast.next.next

        return slow

그 외에 two pointer를 가지고 해결하는 솔루션도 있다.
slow, fast를 각 연결형 리스트의 첫 번째 노드로 두고
fast는 한 번에 2칸, slow는 한 번에 한 칸 이동한다.
2칸 씩 이동하는 빠른 fast 포인터가 연결형 리스트 끝에 도달할 때, slow 포인터는 중간 지점에 도착해 있기 때문에 slow를 반환한다.

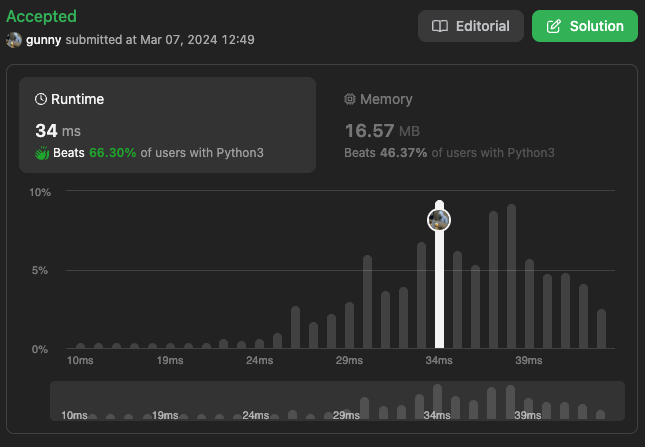
해당 코드의 시간복잡도도 O(n), 공간복잡도도 O(1) 이다.
연결 리스트를 한 번만 순회하는 해당 코드가 더 간단한 것 같다.