[4코3파] #296. Leetcode Binary Search (1)
[4코3파] 1명의 스위프트 개발자가 도망가고 4명의 코틀린 개발자, 3명의 파이썬 개발자의 코딩 테스트 스터디 : 4코3파
START :
[3코1파] 2023.01.04~ (296일차)
[4코1파] 2023.01.13~ (288일차)
[4코3파] 2023.10.01 ~ (26일차)
Today :
2023.10.26 [296일차]
Leetcode Binary Search 문제
[1] 704. Binary Search
문제 설명
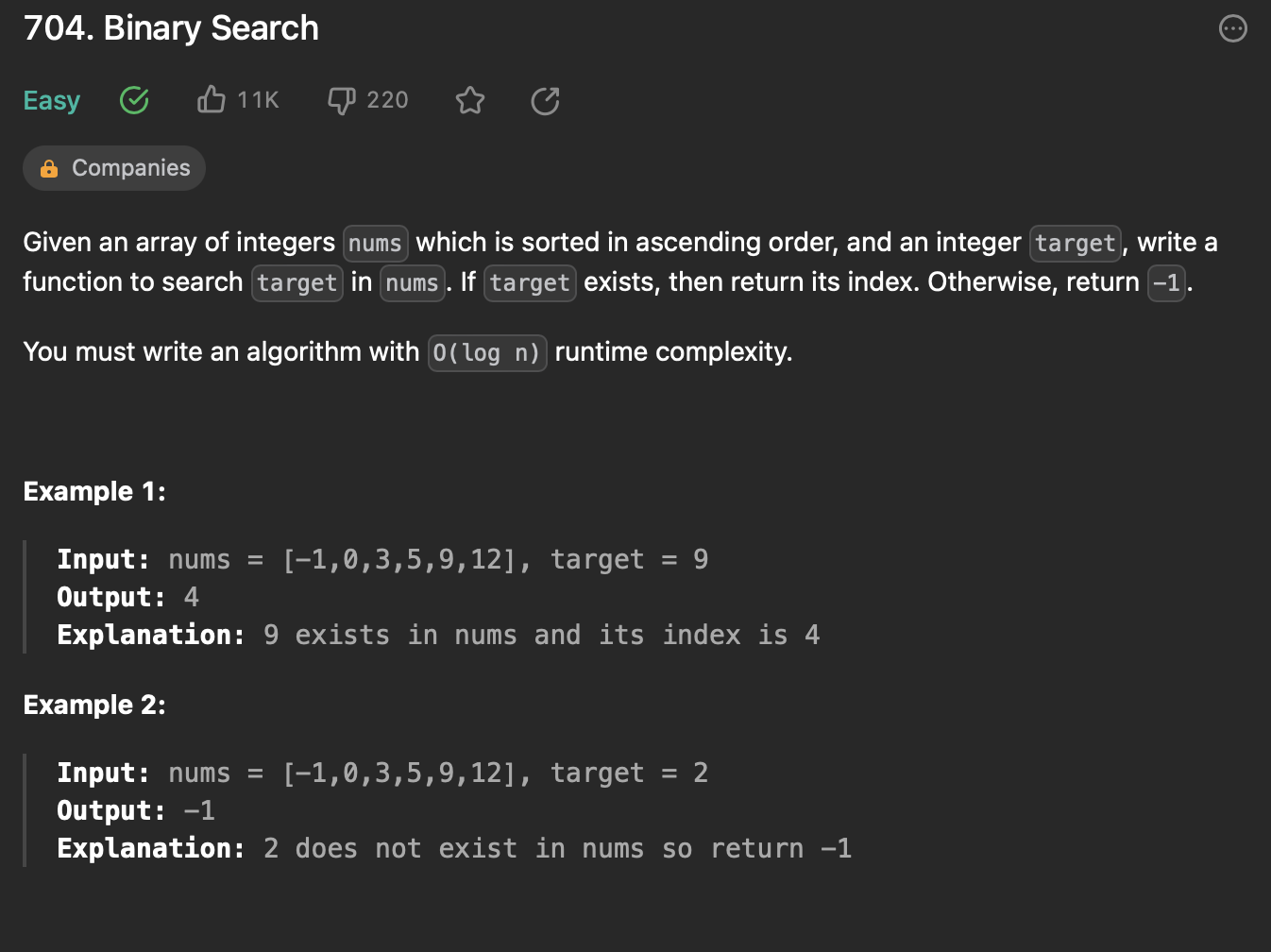
오름차순으로 정렬되어 있는 정수 배열에서 target 을 찾아, 해당 배열의 인덱스를 return한다.
target이 배열에 존재하지 않으면 -1을 반환한다.
문제 풀이 방법
모든 nums 배열을 서치하면 O(n)이지만, binary search로 범위를 좁혀나가면서 찾는 (사전에서 단어 찾는 것처럼) 알고리즘을 사용하면 O(logn)으로 찾을 수 있다.
배열의 시작과 마지막의 중간지점을 찾는 위치로 설정해 해당 원소와 target을 비교하고, target이 더 크다면, 찾기 시작하는 첫 지점을 중간지점바로 뒤로, target이 더 작다면 찾는 범위를 중가지점 바로 전으로 하면서 범위를 좁혀나가면서 찾는다.
내 코드
class Solution:
def search(self, nums: List[int], target: int) -> int:
l, r = 0, len(nums)-1
while l<=r:
mid = l + ((r-l)//2)
if nums[mid] < target:
l = mid+1
elif nums[mid] > target:
r = mid-1
else:
return mid
return -1
[2] 74. Search a 2D Matrix
문제 설명
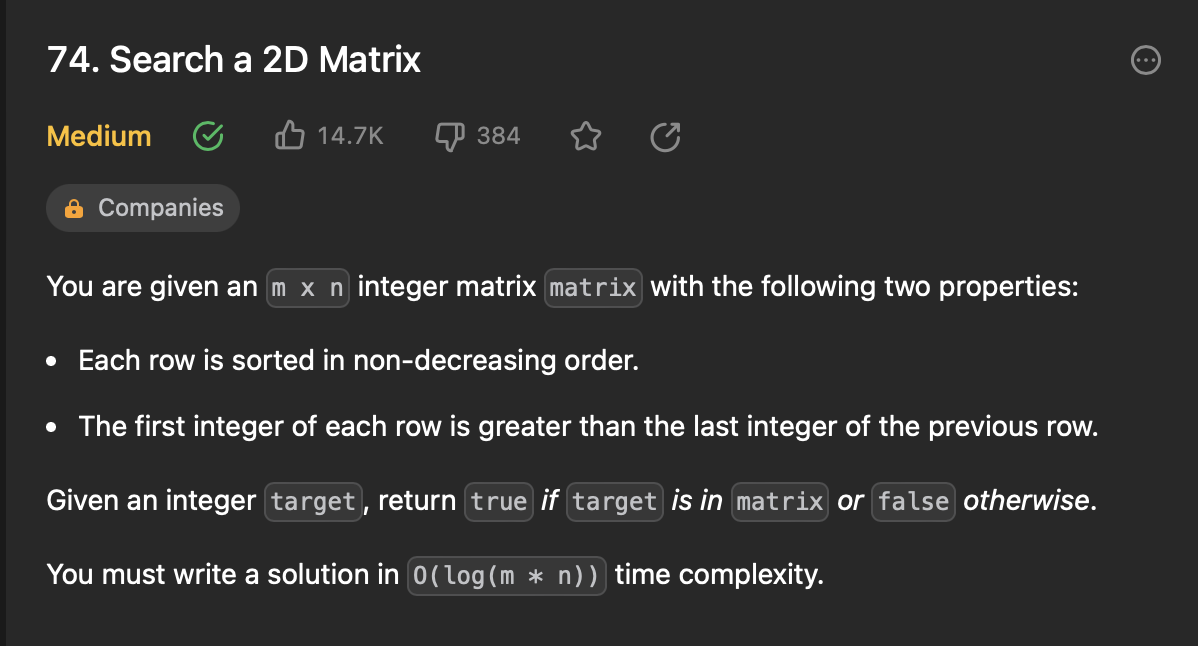
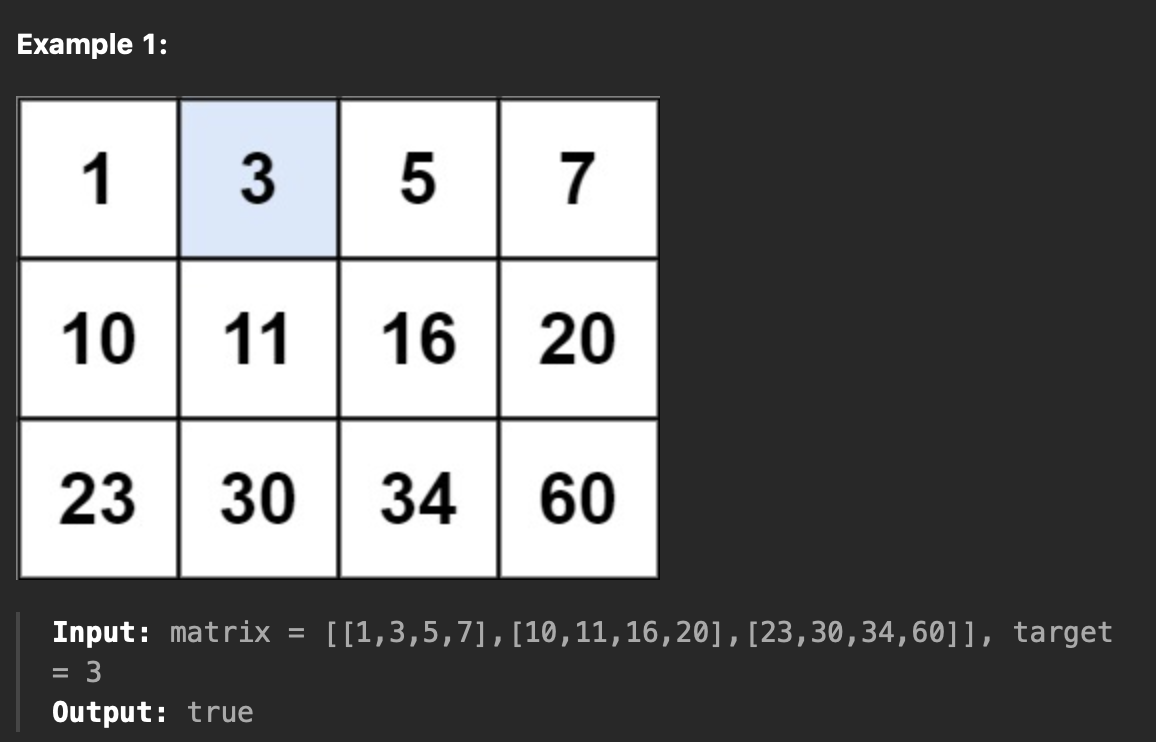
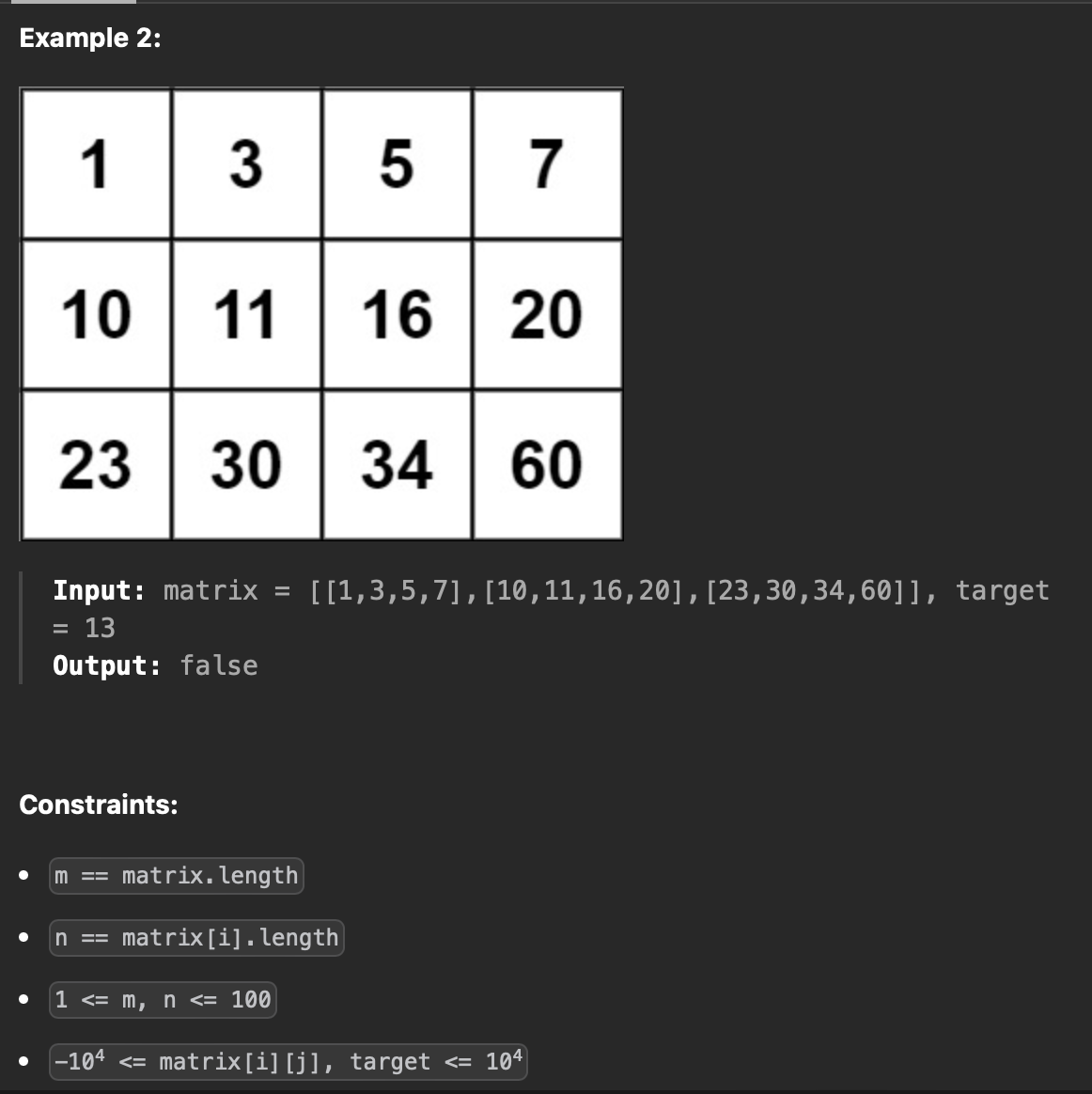
2x2 matrix에서 target 정수가 있으면 True, 없으면 False를 반환함!
시간 복잡도는 O(log(m*n))으로 해결하기!
문제 풀이 방법
모든 행과 열을 돌면서 찾으면 O(mn) 이 나온다.
행을 찾는 것도 binary search, 각 행에서 타겟을 찾는 것도 binary search로 찾으면 O(log(mn)) 으로 풀 수 있다!
내 코드
class Solution:
def searchMatrix(self, matrix: list[list[int]], target: int) -> bool:
ROWS, COLS = len(matrix), len(matrix[0])
top,bot = 0, ROWS-1
while top <= bot:
row = (top+bot)//2
if matrix[row][-1] < target:
top = row+1
elif matrix[row][0] > target:
bot = row-1
else:
break
if not (top <= bot):
return False
l,r = 0, COLS-1
while l<=r:
m = (l+r)//2
if matrix[row][m] < target:
l = m+1
elif matrix[row][m] > target:
r = m-1
else:
return True
return False
[3] 875. Koko Eating Bananas
문제 설명
바나나 개수가 담긴 배열이 주어지고,h 라는 시간이 주어질때
h 시간내에 배열의 바나나를 다 먹을 수 있는 시간 k를 구한다.
문제 풀이 방법
처음에는 무슨 말인가 했는데,,
바나나 다발은 총 배열의 개수 라고 할 때 [3,6,7,11]
각 다발에 달려있는 바나나는 배열의 원소이다.
첫번째 다발은 3개, 두번째 다발은 6개의 바나나가 있는 셈
주어진 시간이 8시간이라고 하면
배열의 모든 바나나를 먹기 위해 소요되는 시간 k를 구해야 하는 것이다.
딱 시간에 맞춰서 먹어야 한다.
예를 들어 바나나 한 다발을 먹는데 5시간이 걸린다고 하면
첫번째 다발은 5시간 내에 3개를 다먹을 수 있으니까 5시간내에 1번 소요
두번째 다발은 5시간 내에 6개를 먹을 수 없다. 그러나 먹기를 시도하는 시간은 5시간으로 고정되어 있으므로 6개를 먹기 위해서는 5시간을 2 번 시도 해야 한다.
세번째 또한 7개를 먹기 위해서는 5시간 2번 소요
이런 식으로 바나나 다발을 다 먹기 위한 시간 k 당 횟수가 h 시간내에 맞는 시간 k를 찾는 것이다.
처음 시도는 l,r를 바나나 다발의 min, max라고 지정했는데 잘 안나왔다. k개가 무조건 바나나 다발의 최소 값보다 낮으라는 보장이 없기 때문에 l을 1로 맞춰주어야 한다!
내 코드
시간복잡도는 이진 검색을 사용하므로, O(log(max(piles)))
공간복잡도는 O(1)이다.
class Solution:
def minEatingSpeed(self, piles: List[int], h: int) -> int:
left, right = 1, max(piles)
ans = right
while left <= right:
mid = (left+right)//2
hours = 0
for p in piles:
hours += math.ceil(p/mid)
if hours <= h:
ans = min(ans, mid)
right = mid-1
else:
left = mid+1
return ans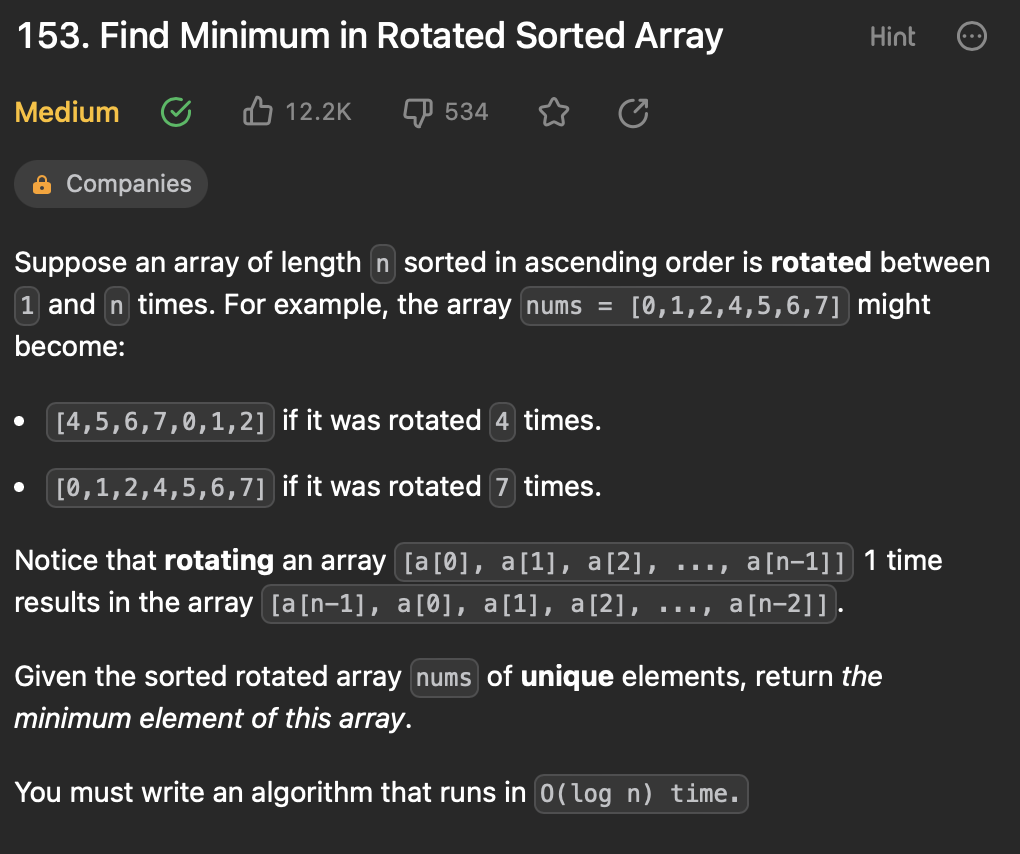
[4] 153. Find Minimum in Rotated Sorted Array
https://leetcode.com/problems/find-minimum-in-rotated-sorted-array/
문제 설명
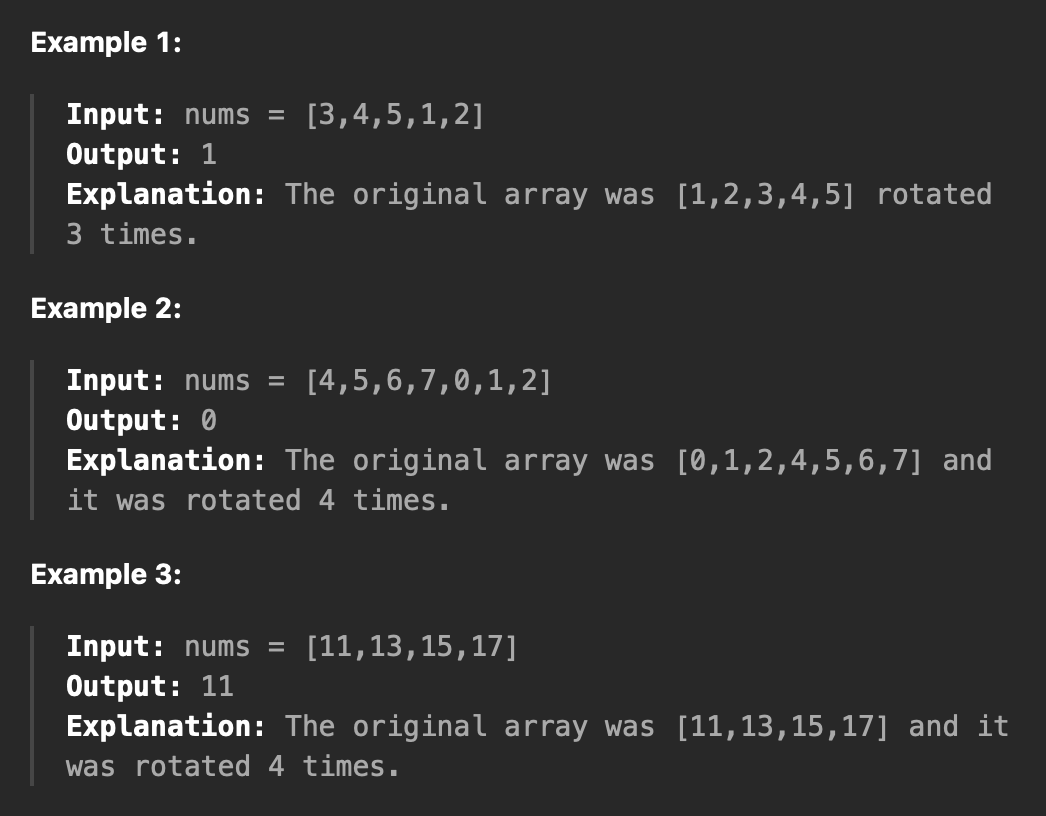
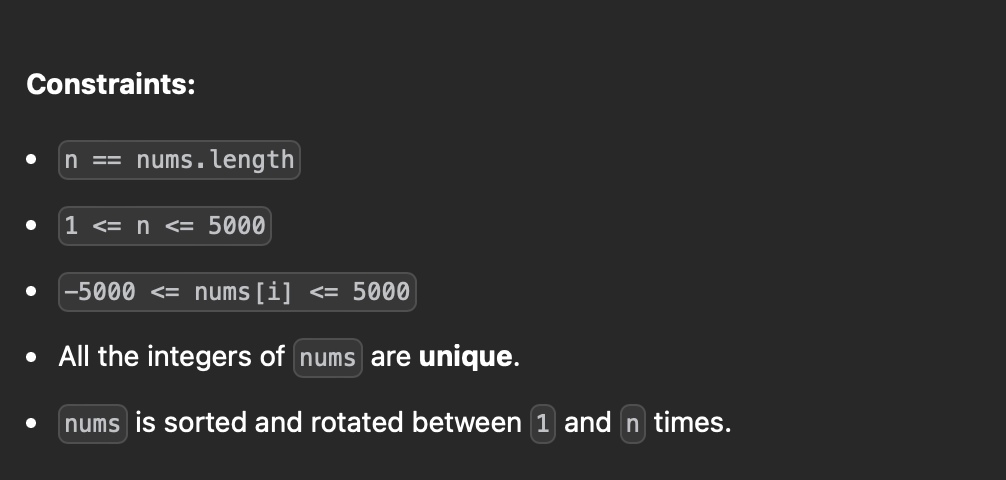
오름차순으로 정렬된 길이 n의 배열이 1회에서 n회 회전된다고 가정한다.
배열 [a[0], a[1], a[2], ..., a[n-1]]을 한 번 회전하면 배열 [a[n-1], a[0]이 됩니다. , a[1], a[2], ..., a[n-2]] 이 된다.
해당 배열에서 가장 작은 원소의 인덱스를 찾아서 return 한다.
O(log n) 시간에 실행되는 알고리즘으로 작성해야 한다.
문제 풀이 방법
주어진 배열 n 에서 특정 원소를 찾기 위해서는 binary search를 이용해야 한다.
그냥 오름차순으로 되어 있으면 left, right, mid를 사용해서 풀면 되는데, 여기서는 오름차순으로 되어 있긴 하지만 배열이 rotate 되어 있어서 어느 시점부터가 시작지점인지를 찾아낸 다음 해당 target을 찾아야 한다..
찾는 방법은 일단은
가장 왼쪽 원소와 가장 오른쪽 원소를 비교해본다.
가장 오른쪽 원소가 왼쪽 원소보다 큰 경우에는 순차적으로 증가하고 있기 때문에 가장 왼쪽 원소를 낮은 원소로 업데이트하고 끝내면된다.
그러나, 그렇지 않은 경우에는 배열을 쪼갠다.
배열의 중간의 원소와 가장 왼쪽원소를 비교해본다.
가장 왼쪽 원소가 배열의 중간 원소보다 작을 경우에는
배열의 왼쪽은 무조건 작은 원소로 구성되어 있는 것으로 가정할 수 있다.
그 이후에 타겟이 왼쪽보다 크고, 가운데 배열보다 클 경우에는
가운데 위치 +1 이 새로운 왼쪽 좌표가 된다.
그러나, 타겟이 가운데 배열보다 작다면 가운데 위치-1이 새로운 오른쪽 좌표가 된다.
이러한 식으로 왼쪽, 오른쪽을 업데이트 해가는 binary search를 해가면서, 탐색하면서 배열의 최소값을 업데이트 해간다.
내 코드
lass Solution:
def findMin(self, nums: List[int]) -> int:
ans = nums[0]
l,r = 0, len(nums)-1
while l<=r:
if nums[l] < nums[r]:
ans = min(ans, nums[l])
break
mid = (l+r)//2
ans = min(ans, nums[mid])
if nums[l] <= nums[mid]:
l = mid+1
else:
r = mid-1
return ans여담
binary search 7문제 풀어야 하는데
오늘 이벤트가 있어서 4문제 밖에 못풀었네..
나머지 3문제는 지금부터 풀고 자야겠다
