[4코3파] 1명의 스위프트 개발자가 도망가고 4명의 코틀린 개발자, 3명의 파이썬 개발자의 코딩 테스트 스터디 : 4코3파
START :
[3코1파] 2023.01.04~ (300일차)
[4코1파] 2023.01.13~ (292일차)
[4코3파] 2023.10.01 ~ (30일차)
Today :
2023.10.30 [300일차]
Leetcode Trees
[1] 226. Invert Binary Tree
https://leetcode.com/problems/invert-binary-tree/description/
문제 설명
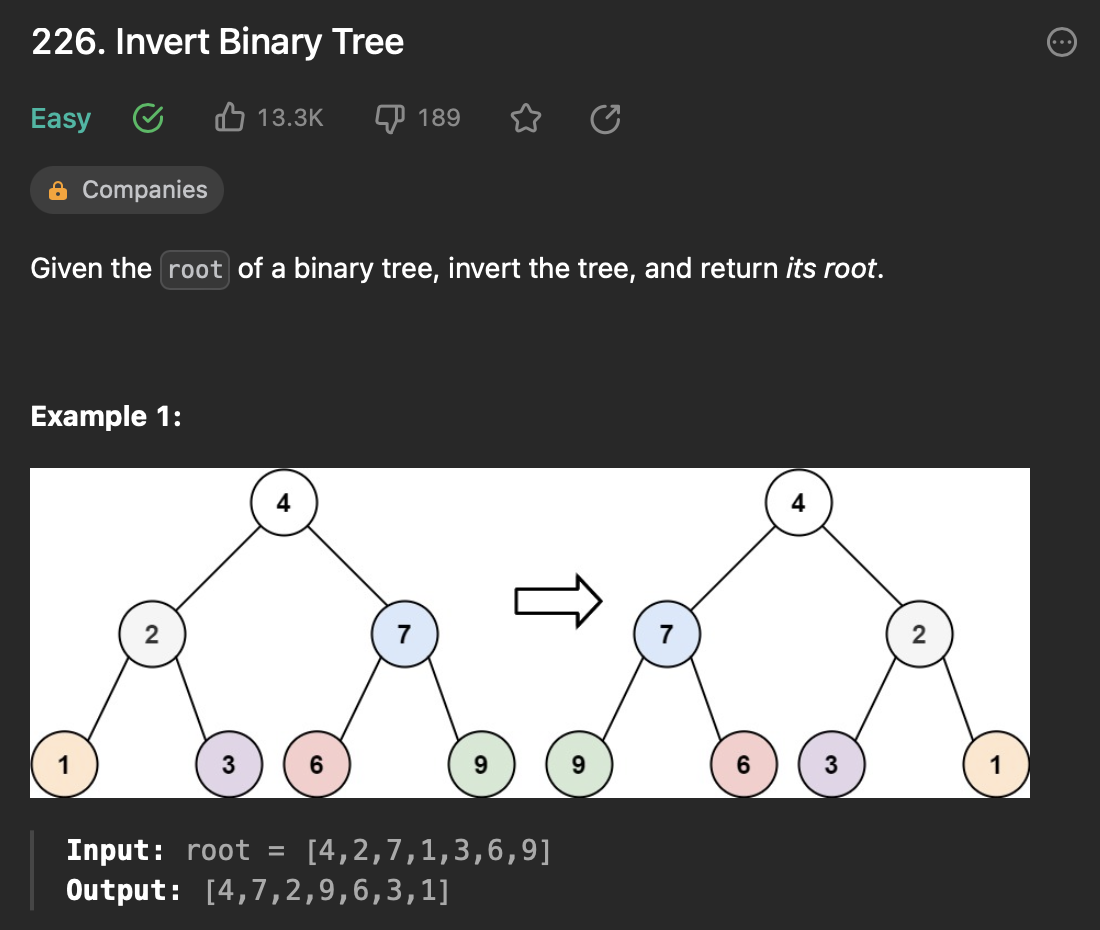
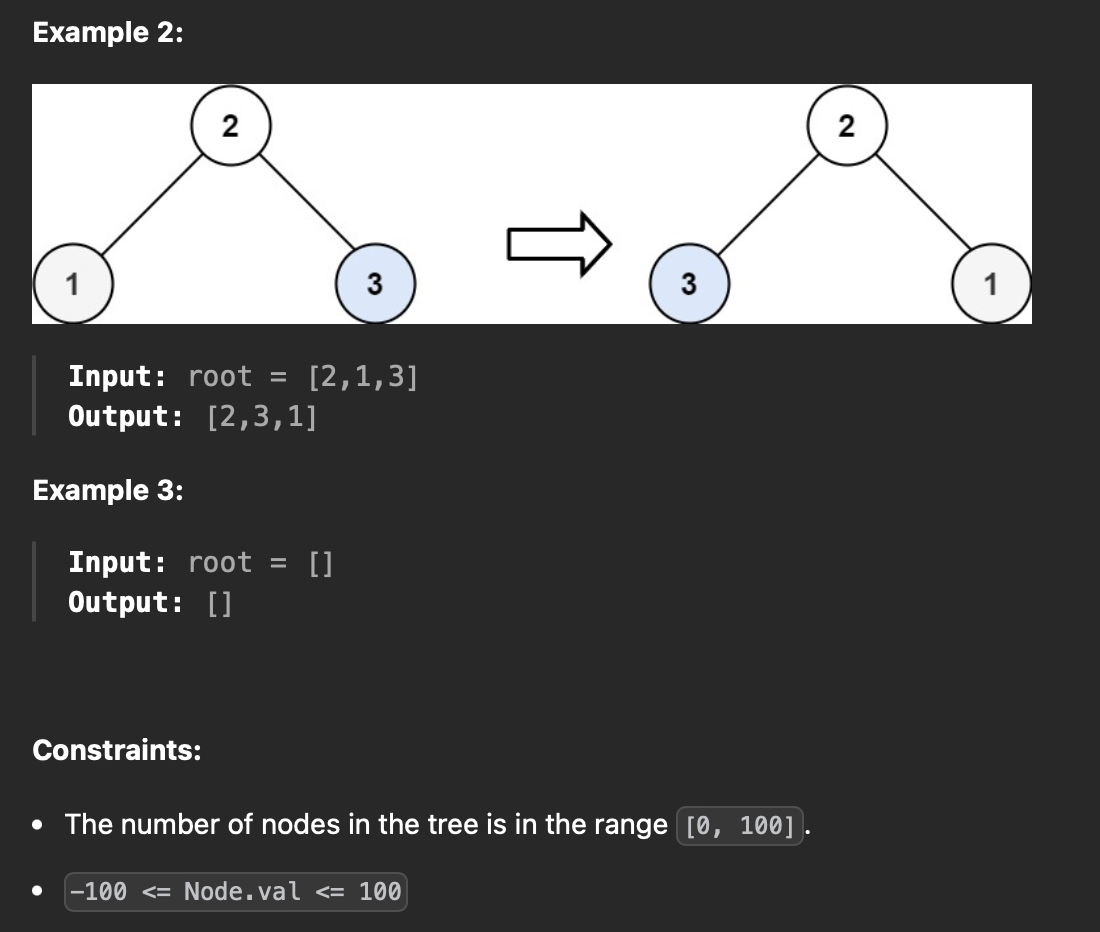
주어진 이진 트리의 left node와 right node를 뒤집은 이진 트리로 반환하기
문제 풀이 방법
dfs로 루트 노드에서 왼쪽 노드로 계속 파고 들어가서 마지막 터미널 노드가 나올 때까지 왼쪽 노드로 들어가면서 오른쪽 노드와 reverse 한다.
내 코드
n : 노드의 크기, L: 왼쪽 노드, R: 오른쪽노드
시간복잡도는 O(n)
공간복잡도는 O(max(L,R))
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
if not root:
return None
tmp = root.left
root.left = root.right
root.right = tmp
self.invertTree(root.left)
self.invertTree(root.right)
return root
[2] 104. Maximum Depth of Binary Tree
문제 설명
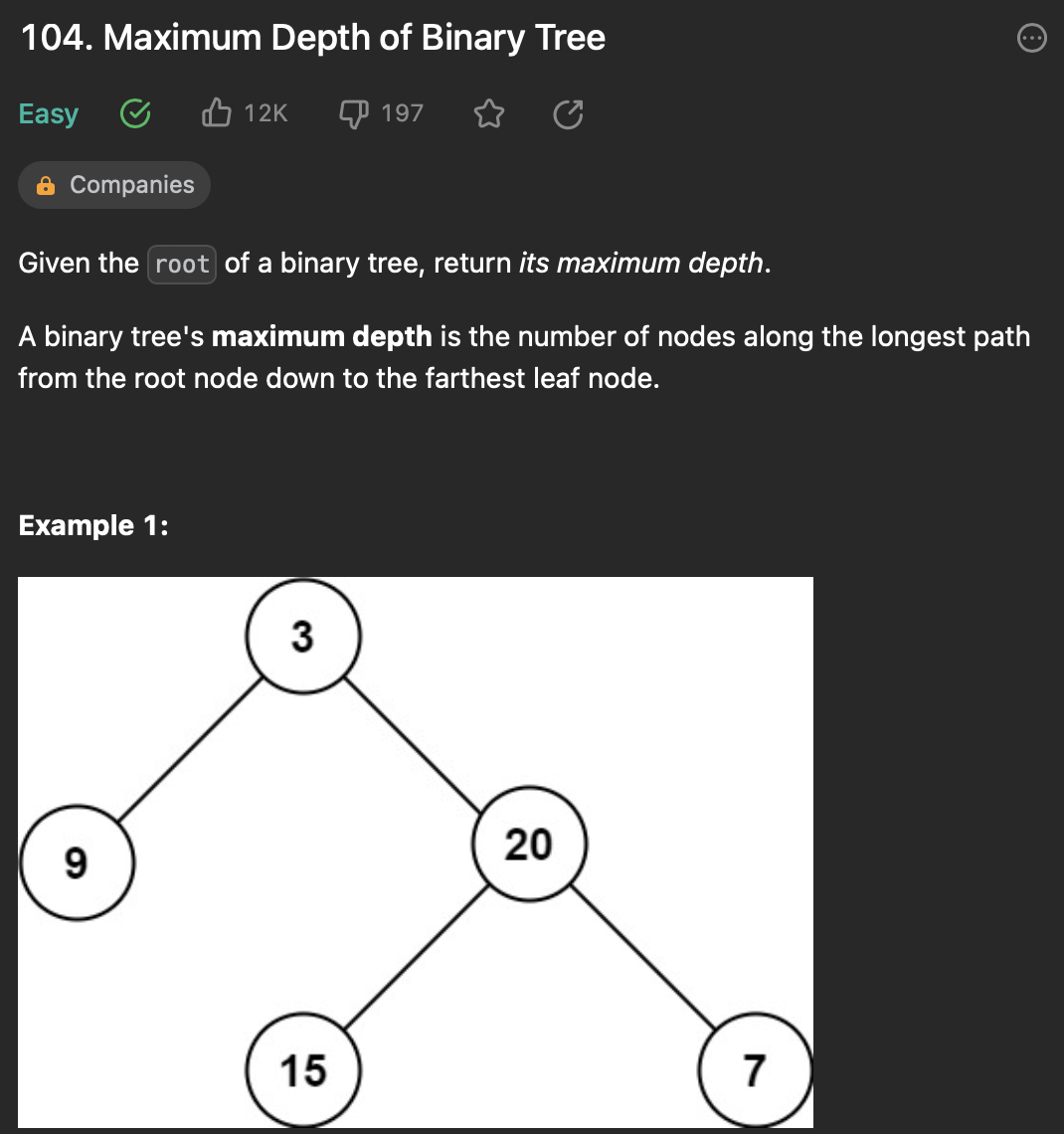
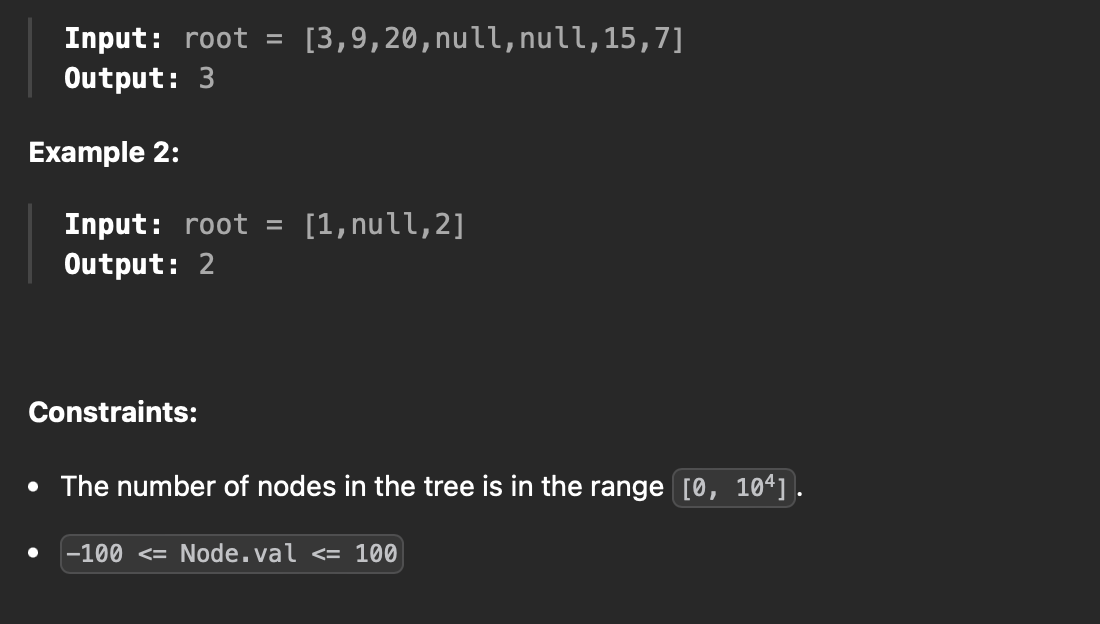
주어진 이진트리의 최대 깊이를 반환하기
문제 풀이 방법
dfs로 트리를 계속 내려가면서, left, right의 최대 깊이를 탐색하면서 깊이를 업데이트 해간다.
해당 문제를 푸는 방법은
stack, dfs, bfs 등 다양한 방법으로 풀 수 있다.
내 코드
일단 dfs로 푼 코드
시간복잡도는 O(n), n은 노드의 수
원래 노드의 높이에 달려 있어 공간복잡도는 O(H), h는 노드의 높이이다. 균형잡힌 이진 트리라고 한다면 공간복잡도는 O(logN) 이다.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
def dfs(root):
if not root:
return 0
left = dfs(root.left)
right = dfs(root.right)
return 1+max(left,right)
return dfs(root)
[3] 543. Diameter of Binary Tree
문제 설명

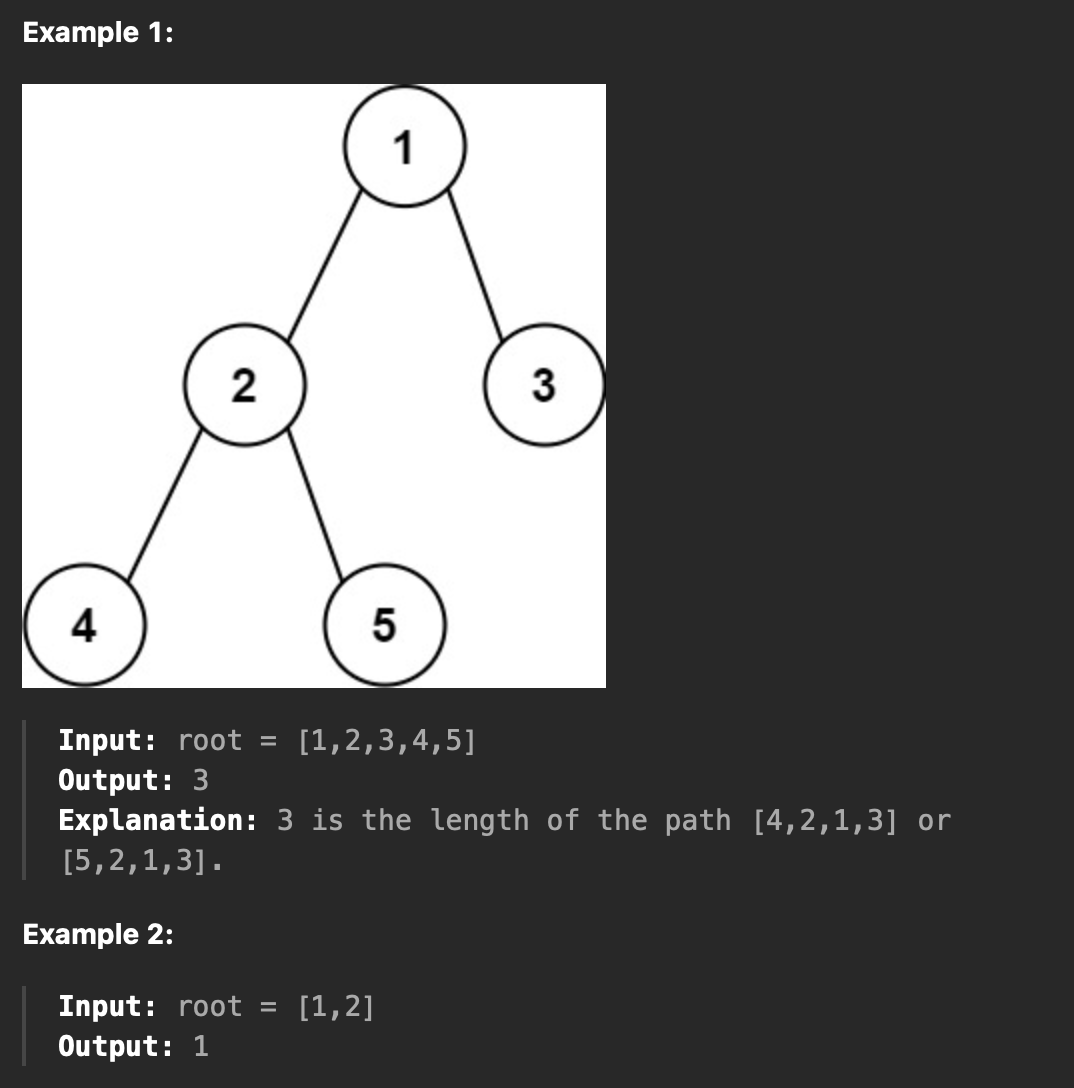

이진 트리의 루트가 주어지면 트리 지름의 길이를 반환한다.
문제 풀이 방법
각 루트 노드에서의 지름은 왼쪽 노드와, 오른쪽 노드의 최대 길이를 더한 것이다.
왼쪽 노드의 길이, 오른쪽 노드의 길이는 각 노드들의 높이이고, dfs를 통해서 아래로 내려가면서, 터미널 노드부터 각 높이를 계산하면서 부모 노드로 올라오면서 합산 한후, 최종 가장 긴 트리의 지름을 업데이트 한다.
내 코드
시간복잡도는 O(n), 공간복잡도는 O(h)
n은 노드의 수, h는 노드의 높이이다.
해당 노드가 균형이진트리라면 공간복잡도는 O(logN)
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def diameterOfBinaryTree(self, root: Optional[TreeNode]) -> int:
ans = [0]
def dfs(root):
if not root:
return 0
left = dfs(root.left)
right = dfs(root.right)
ans[0] = max(ans[0], left+right)
return 1+max(left, right)
dfs(root)
return ans[0]
[4] 110. Balanced Binary Tree
문제 설명
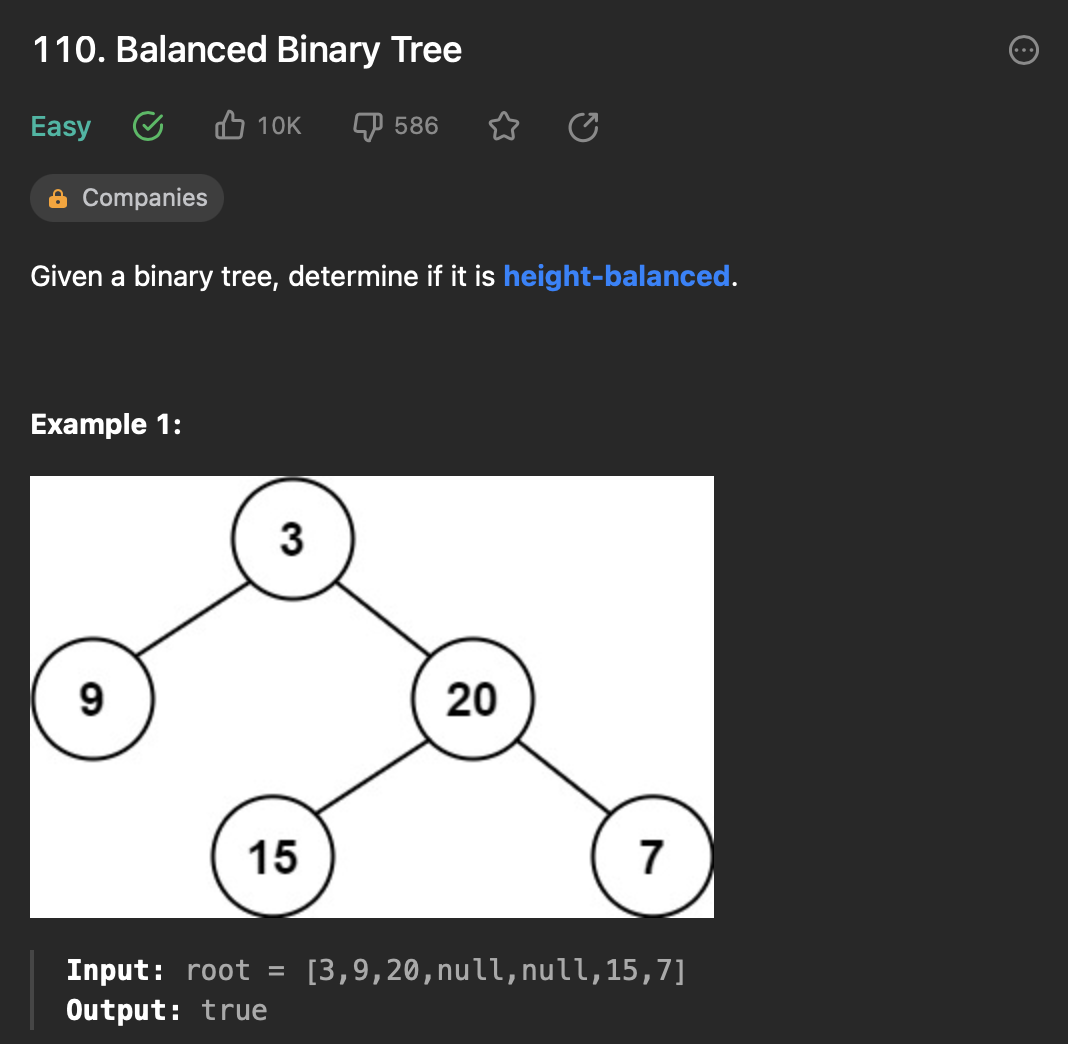

주어진 트리가 균형 이진 트리 이면 True, 아니면 False를 return 한다.
균형 이진 트리는 모든 노드의 두 하위 트리 깊이가 1 이상 넘지 않는 트리이다.
문제 풀이 방법
dfs로 노드의 끝까지 타고 들어가면서, 노드의 깊이를 확인하고 현재 있는 노드에서 균형 잡혀 있는지 왼쪽과 오른쪽 노드의 깊이를 확인하면서 업데이트 한다.
노드의 높이를 확인했던 알고리즘과 유사하지만 여기서 왼쪽과 오른쪽 노드의 높이의 차이가 1이상인지 아닌지를 체크하는 balance 변수를 하나 더 저장하면서 업데이트 하면서 위로 올라간다.
거슬러 올라가서 마지막 루트 노드에서 False 라면 균형 이진 트리가 아니고,
True 라면 균형 이진 트리가 된다.
내 코드
시간복잡도는 O(n), 공간복잡도는 O(h)이다.
n은 노드의 수, h는 노드의 높이이다.
해당 트리가 균형 이진 트리라면 공간복잡도는 O(logN)이다.
class Solution:
def isBalanced(self, root: Optional[TreeNode]) -> bool:
def bfs(root):
if not root:
return [True, 0]
left = bfs(root.left)
right = bfs(root.right)
balanced = (left[0] and right[0] and abs(left[1]-right[1]) <= 1)
return [balanced, 1+max(left[1],right[1])]
return bfs(root)[0]
[5] 100. Same Tree
문제 설명
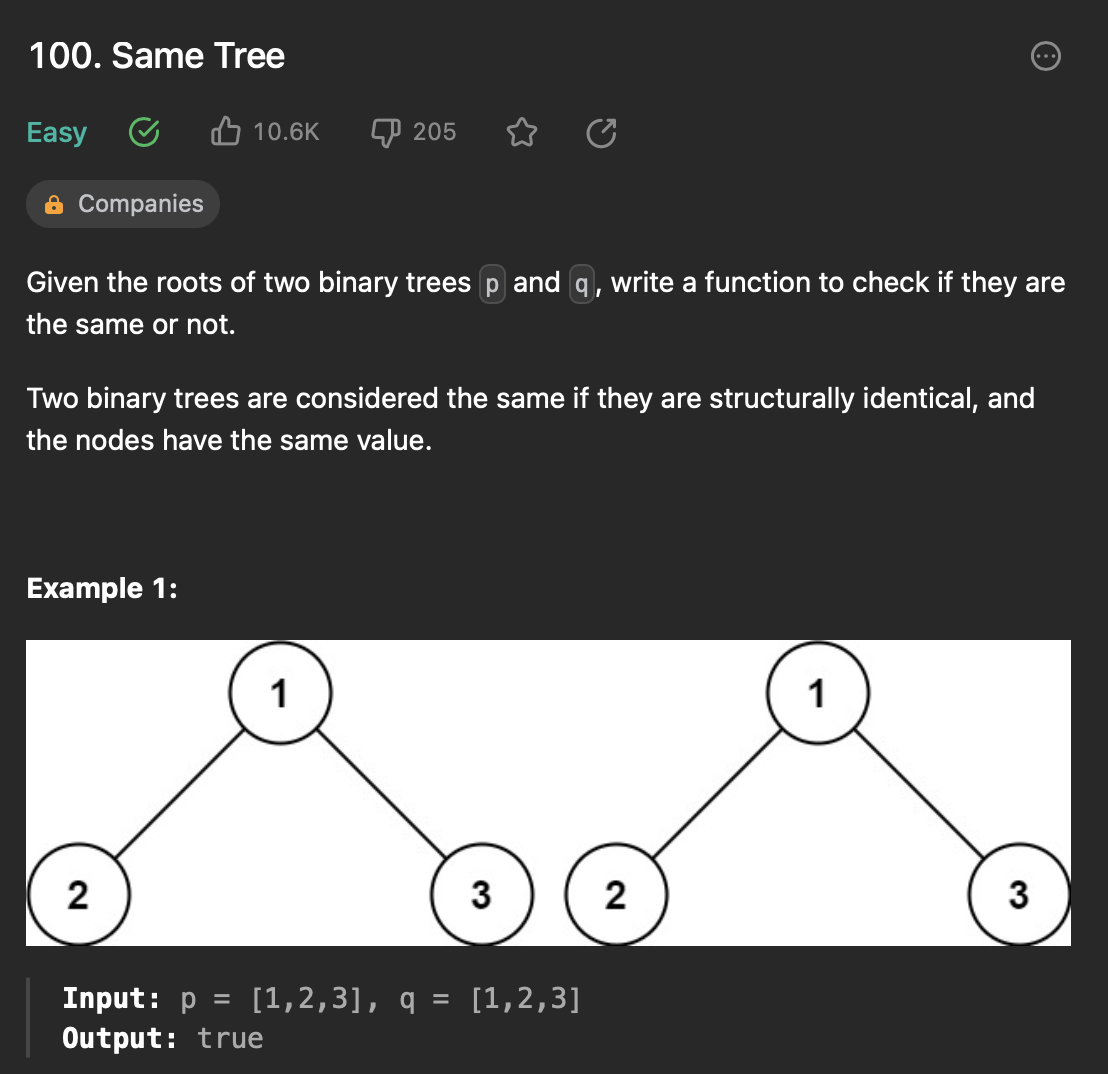
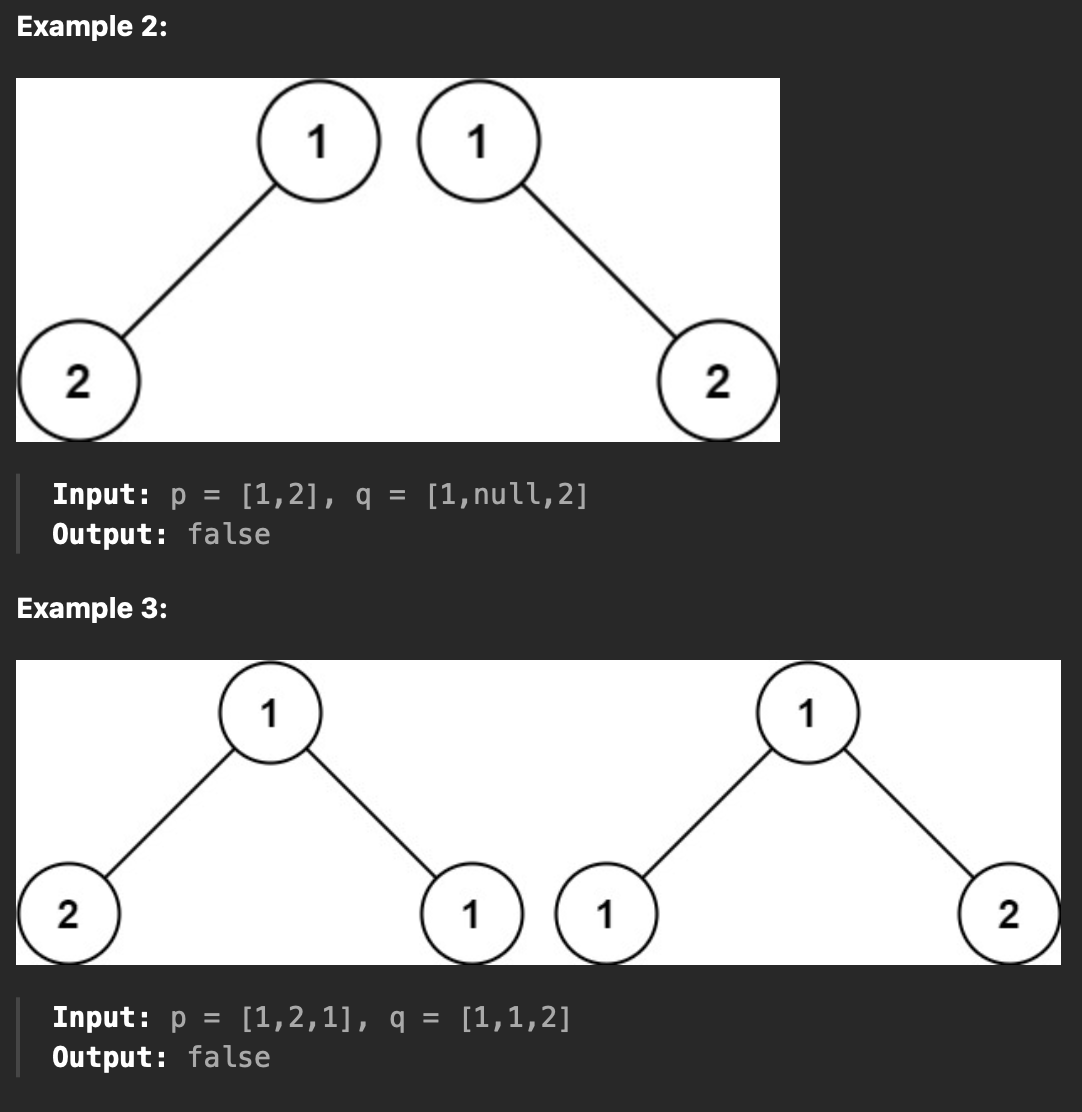
두 개의 트리가 주어질 때, 해당 트리가 같으면 true, 아니면 False를 반환한다.
문제 풀이 방법
두 트리를 루트 노드부터 같이 이동시켜 나가면서 left 노드의 값이 같은지 비교, right 노드의 값이 같은지를 트리로 내려가면서 업데이트 한다.
중간에 다르면 False를 return 하고,
마지막 노드 까지 계속 내려가서 같으면 True를 리턴한다.
내 코드
공간복잡도는 O(N)
시간복잡도 O(H) -> 노드의 높이
균형 이진 트리라면 O(logN)
class Solution:
def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:
if not q and not p:
return True
if q and p and q.val == p.val:
return (self.isSameTree(q.left, p.left) and self.isSameTree(q.right, p.right))
else:
return False
[6] 572. Subtree of Another Tree
문제 설명
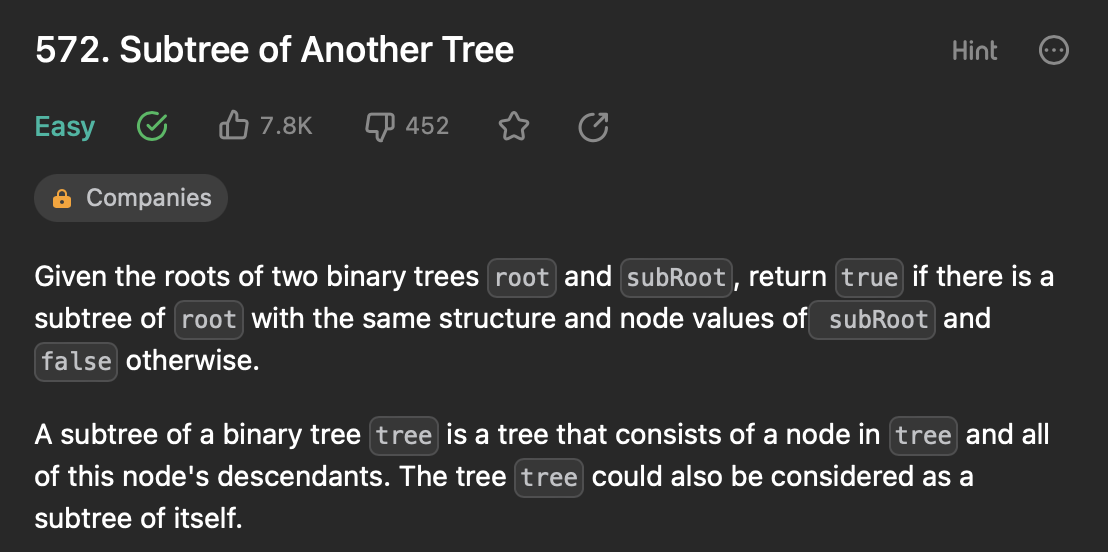
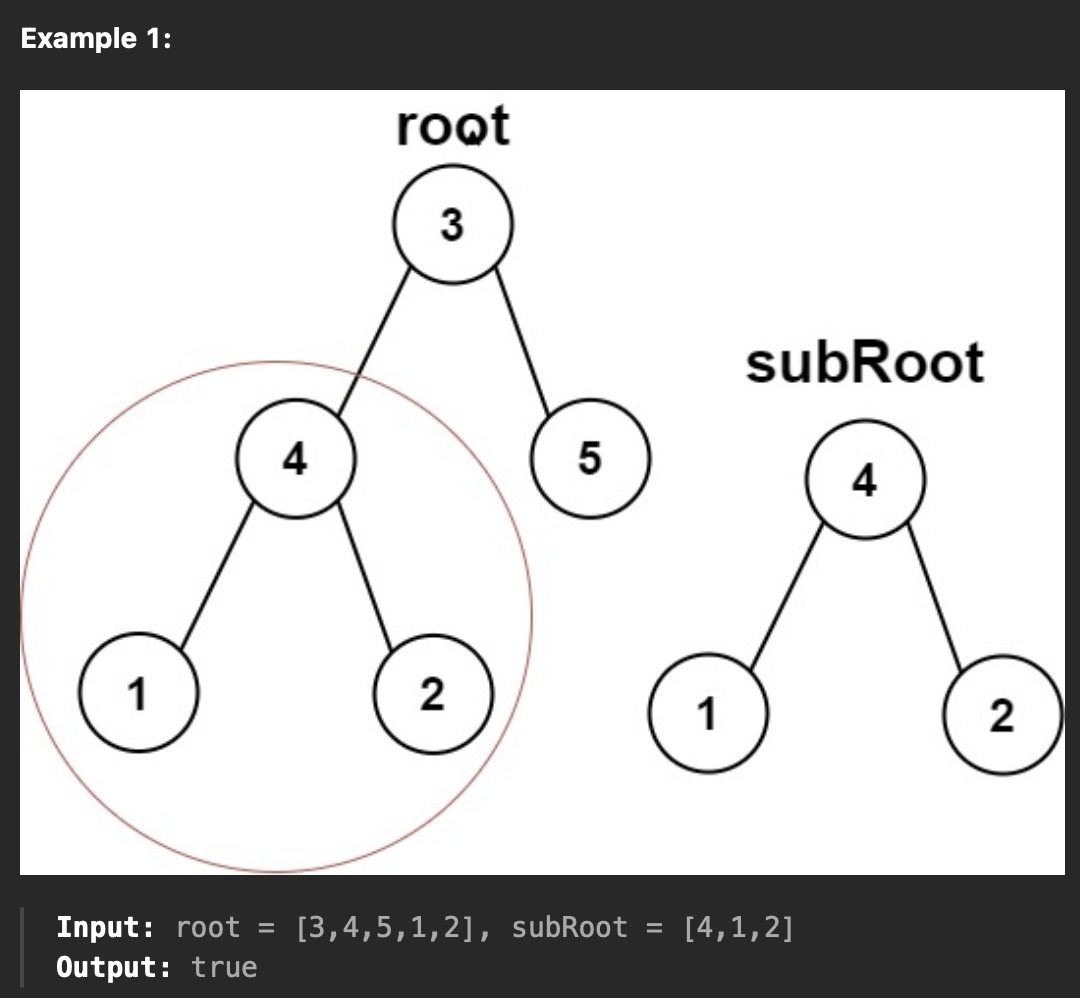
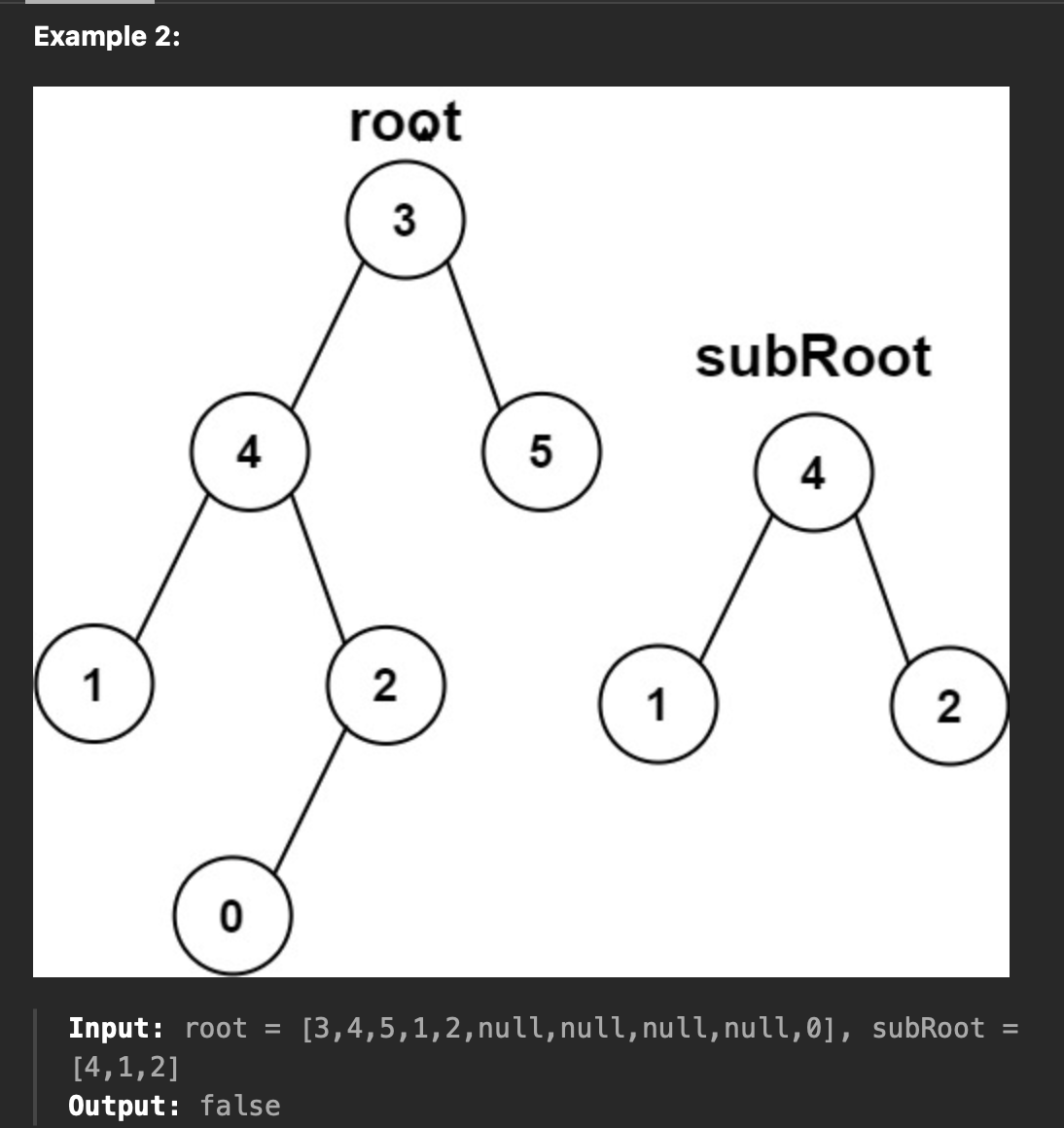
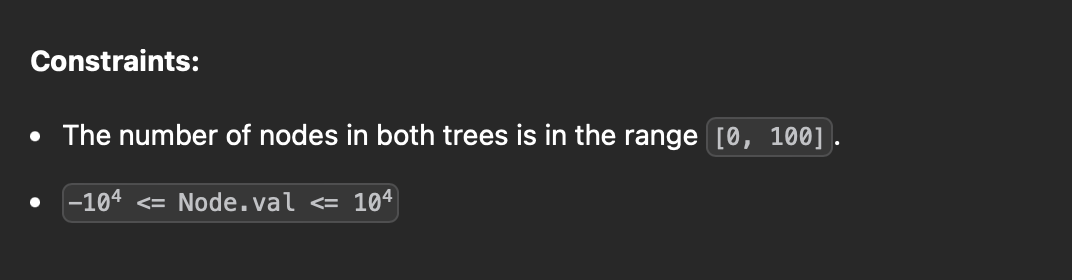
두개의 노드 root, subroot가 주어 질때 subroot가 root 내의 부분 node 이면 return, 아니면 false를 반환한다.
문제 풀이 방법
노드가 서로 같은지 아닌지 확인하는 동일 트리 메소드를 하나 생성한다.
메인 솔루션의 메소드에서는 엣지케이드들을 명시하는데, 엣지케이스는 subtree가 null 인 경우
root가 null 인 경우 등이 있다.
전자의 경우에는 true, 후자의 경우에는 False이다.
처음 주어진 root와 subroot가 같은지 앞서 생성했던 동일 트리메소드로 확인하고, root의 left 노드, root의 right 노드와 subroot 중 하나가 동일 트리 메소드라면 true를 반환하도록 재귀로 설계한다.
내 코드
sameTree 함수는 isSubtree 함수에서 재귀적으로 호출되서, 모든 노드를 확인하므로 O(N)이고,
여기서 N은 root 트리의 노드 수
각 sameTree 호출은 최악의 경우 subRoot 트리의 모든 노드와 root 트리의 모든 노드를 비교하게 되므로, 해당 비교 작업도 O(N)이므로,
따라서 전체 코드의 시간 복잡도는 O(N^2)이다.
공간복잡도는 O(H), 노드의 높이이고, 균형 이진트리라면 O(logN)이다.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isSubtree(self, root: Optional[TreeNode], subRoot: Optional[TreeNode]) -> bool:
if not subRoot:
return True
if not root and subRoot:
return False
if self.sameTree(root,subRoot):
return True
return (self.isSubtree(root.left, subRoot) or self.isSubtree(root.right,subRoot))
def sameTree(self, r, s):
if not r and not s:
return True
if r and s and r.val == s.val:
return (self.sameTree(r.left, s.left) and self.sameTree(r.right, s.right))
return False
[7] 102. Binary Tree Level Order Traversal
https://leetcode.com/problems/binary-tree-level-order-traversal/
문제 설명
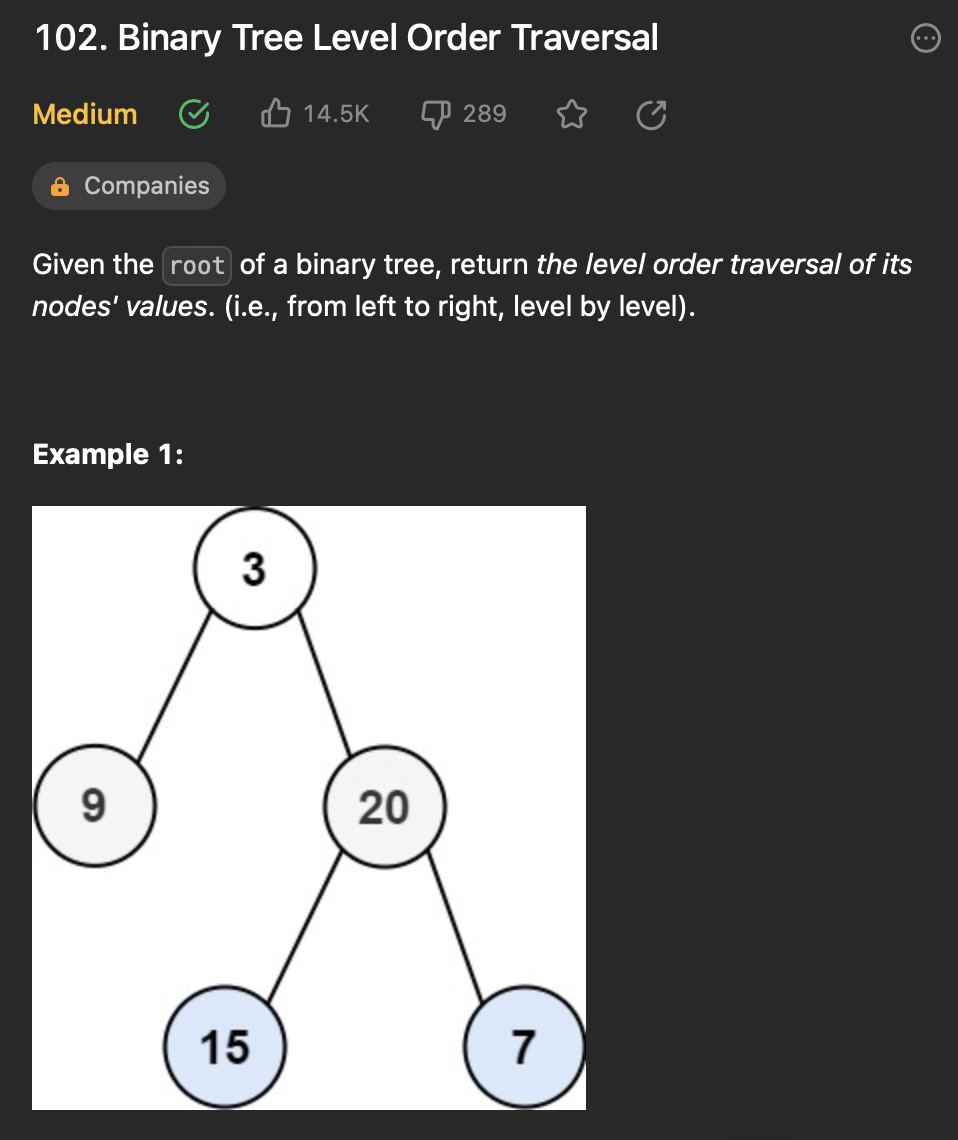
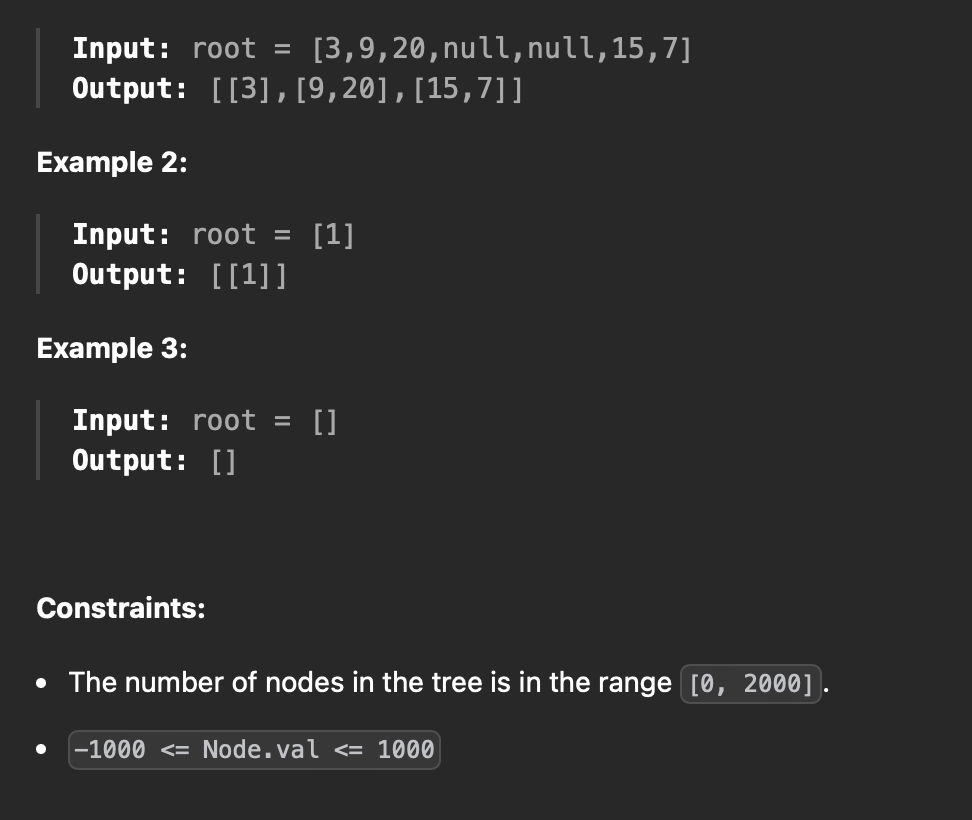
문제 풀이 방법
내 코드
from collections import deque
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
ans = []
queue = deque()
queue.append(root)
while queue:
qLen = len(queue)
level = []
for i in range(qLen):
node = queue.popleft()
if node:
level.append(node.val)
queue.append(node.left)
queue.append(node.right)
if level:
ans.append(level)
return ans[8] 199. Binary Tree Right Side View
문제 설명
이진 트리를 오른쪽 측면에서 바라 볼때,
눈에 보이는 트리의 원소만 리턴함
문제 풀이 방법
bfs로 트리의 한 level 씩 search 하면서, 왼쪽 노드의 값, 오른쪽 노드 순으로 값을 탐색하면서 현재의 노드의 값을 업데이트한다.
오른쪽 측면에서 바라본다면, 같은 level 에서 오른쪽 노드가 있으면 오른쪽 노드의 원소만 보일 것이고, 오른쪽 노드가 없다면 왼쪽 노드의 원소만 보일 것이다.
각 level의 탐색이 끝나면 마지막 업데이트 되어 있는 원소의 값을 리스트에 넣고 최종적으로 모든 노드의 레벨이 탐색되면 각 레벨에서 마지막에 있던 원소를 넣은 리스트를 반환한다.
내 코드
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def rightSideView(self, root: Optional[TreeNode]) -> List[int]:
ans = []
queue = collections.deque([root])
while queue:
rightVal = None
for i in range(len(queue)):
node = queue.popleft()
if node:
rightVal = node.val
queue.append(node.left)
queue.append(node.right)
if rightVal !=None:
ans.append(rightVal)
return ans
[9] 105. Construct Binary Tree from Preorder and Inorder Traversal
https://leetcode.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/
문제 설명
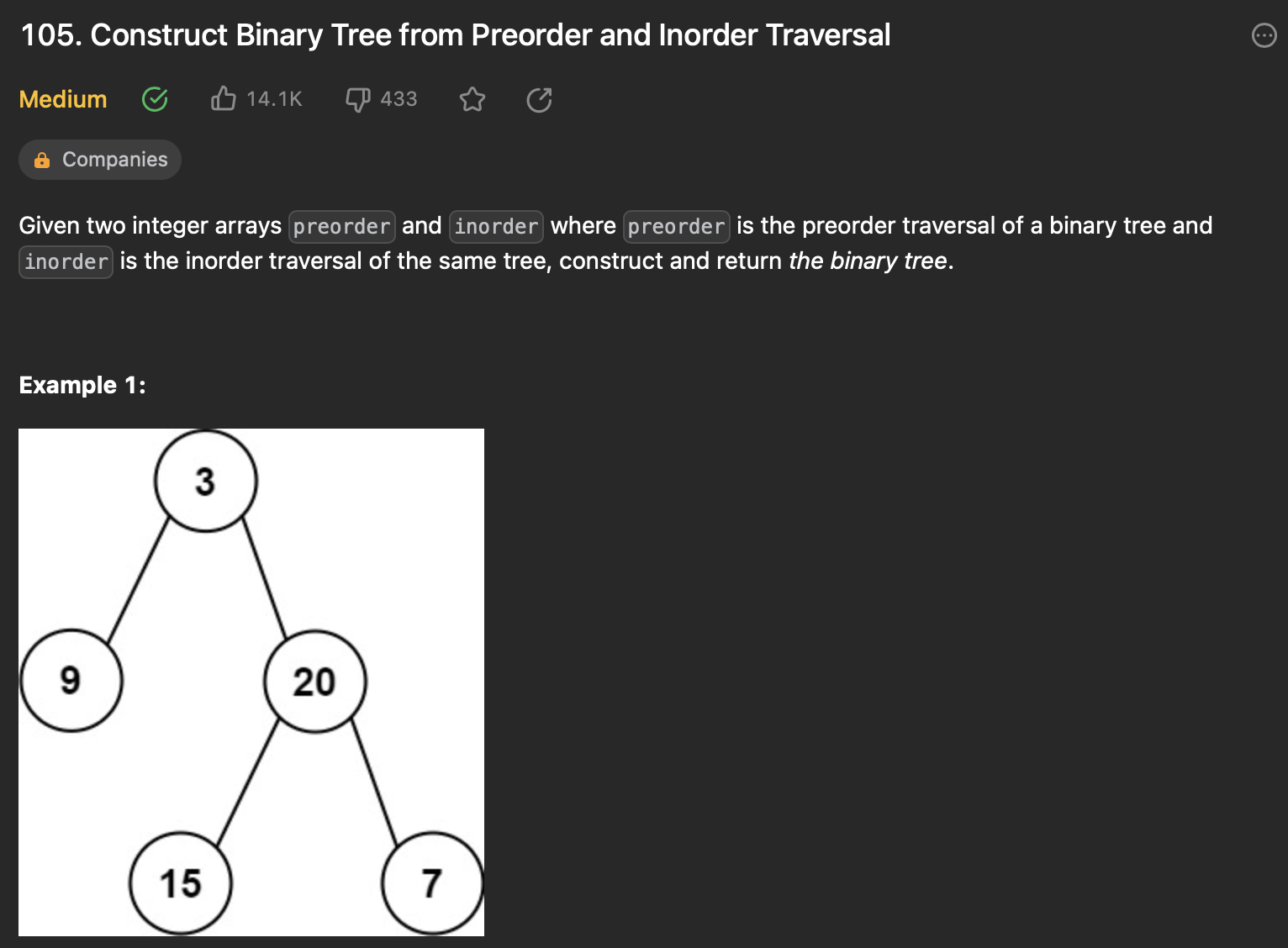
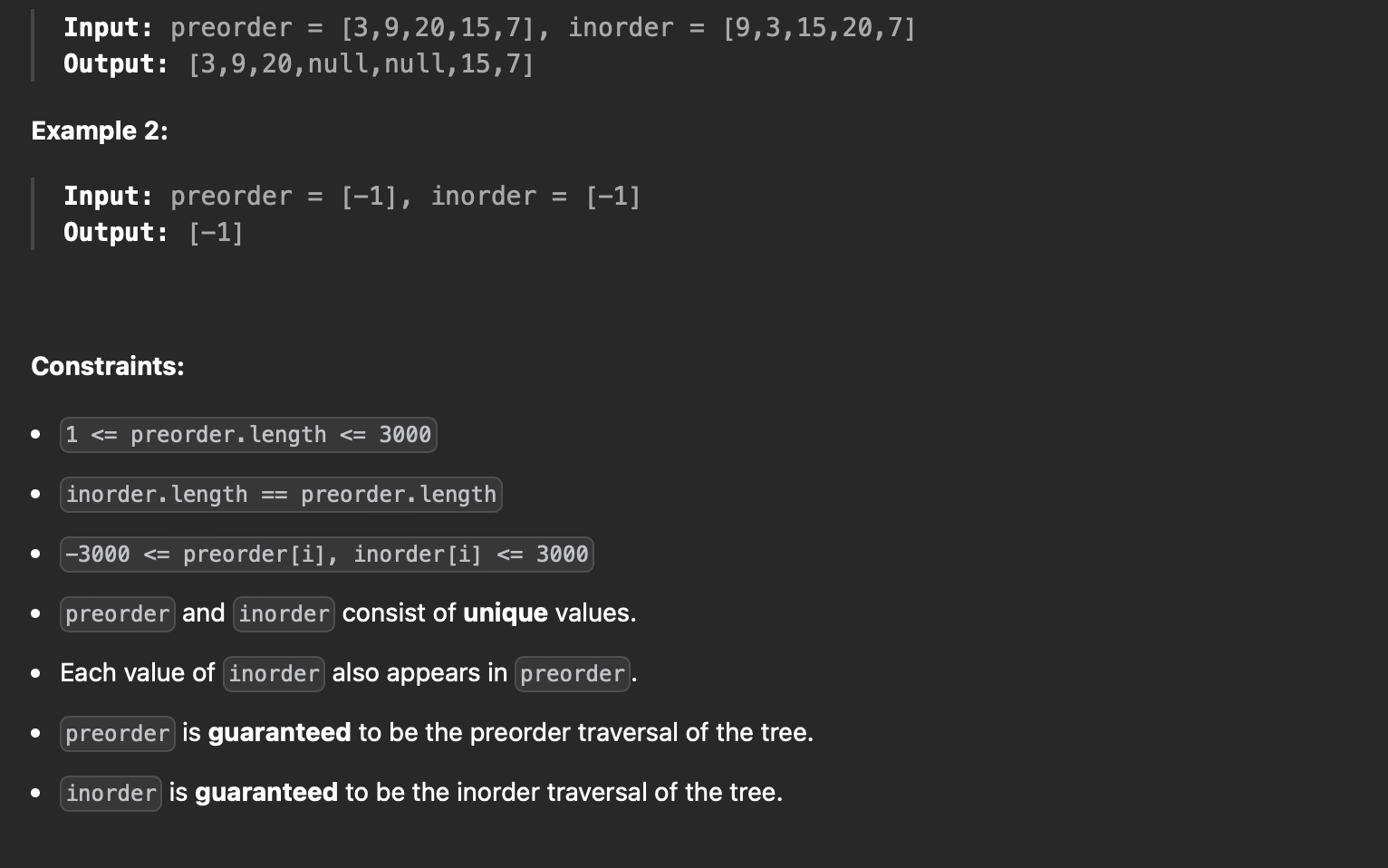
어떤 트리의 preorder 방식으로 탐색한 원소들을 저장한 배열과, inorder 방식으로 탐색한 원소들을 저장한 배열이 주어질 때, 해당 preorder, inorder의 배열을 보고 원래의 트리 구조로 반환하기
문제 풀이 방법
preorder의 경우 트리 탐색 위치는 루트노드 -> 왼쪽 노드 -> 오른쪽 노드 순이고
inorder의 경우 트리 탐색 위치는 왼쪽 노드 -> 루트 노드 -> 오른쪽 노드 순이다.
즉, 주어진 preorder의 가장 첫번째 원소는 무조건 루트 노드를 의미한다.
그래서 제일 preorder의 가장 첫번째 원소를 루트 노드라고 생각한 후, 이제 왼쪽과 오른쪽 노드에 어떤 원소가 있는지 확인하기 위해서는 inorder를 이용하는데,
inorder에서 루트 노드의 인덱스를 찾은 후에 인덱스 기준 왼쪽에 위치하면 왼쪽 노드의 원소이고, 오른쪽에 위치하면 오른쪽 노드의 원소라고 생각하면 된다.
이런 식으로 recursive 하게 왼쪽, 오른쪽 노드를 업데이트해 가면서 원래의 노드 형식을 리턴한다.
내 코드
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
if not preorder and not inorder:
return None
root = TreeNode(preorder[0])
mid = inorder.index(preorder[0])
root.left = self.buildTree(preorder[1:mid+1],inorder[:mid])
root.right = self.buildTree(preorder[mid+1:], inorder[mid+1:])
return root
[10] 1448. Count Good Nodes in Binary Tree
https://leetcode.com/problems/count-good-nodes-in-binary-tree/
문제 설명
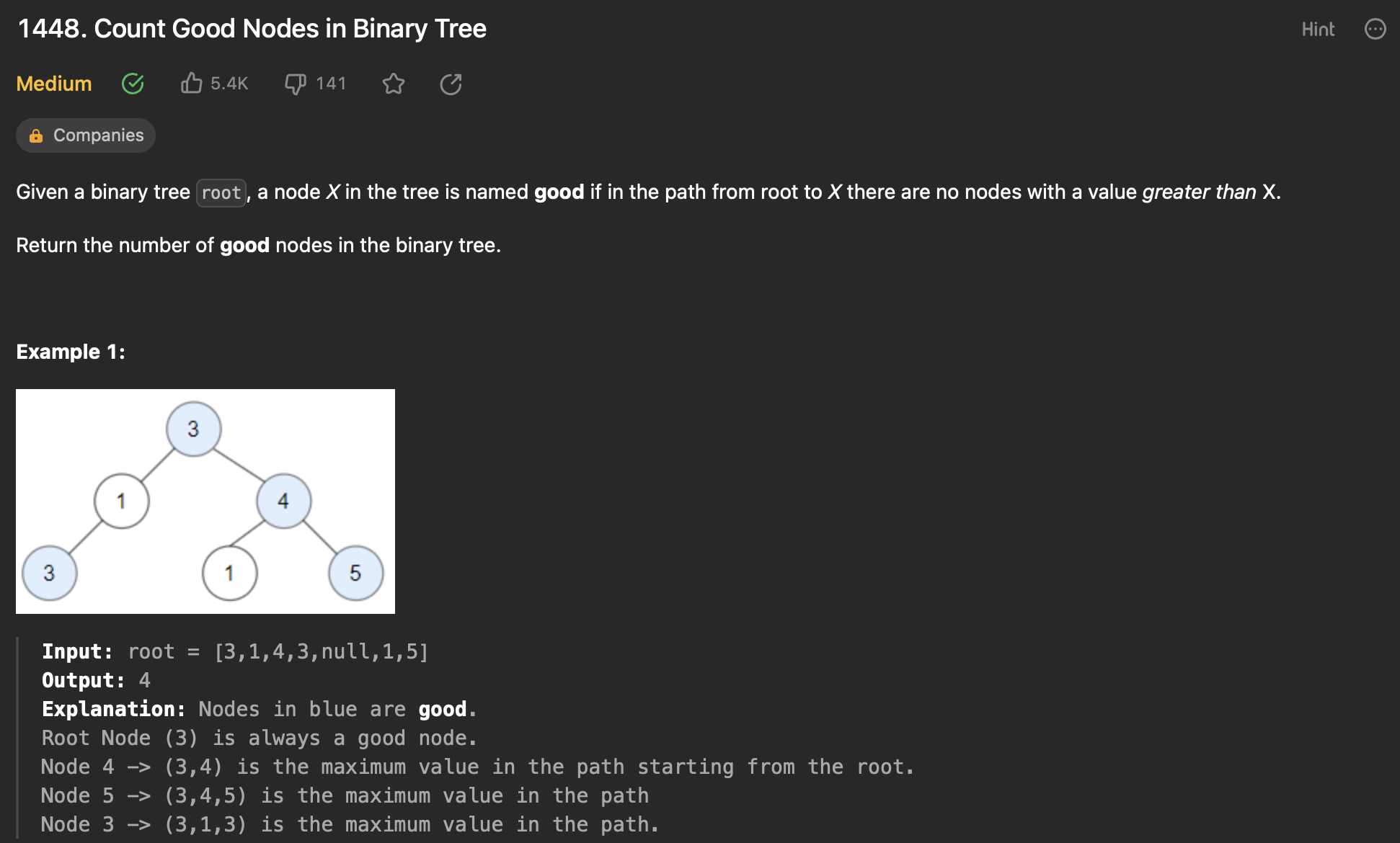
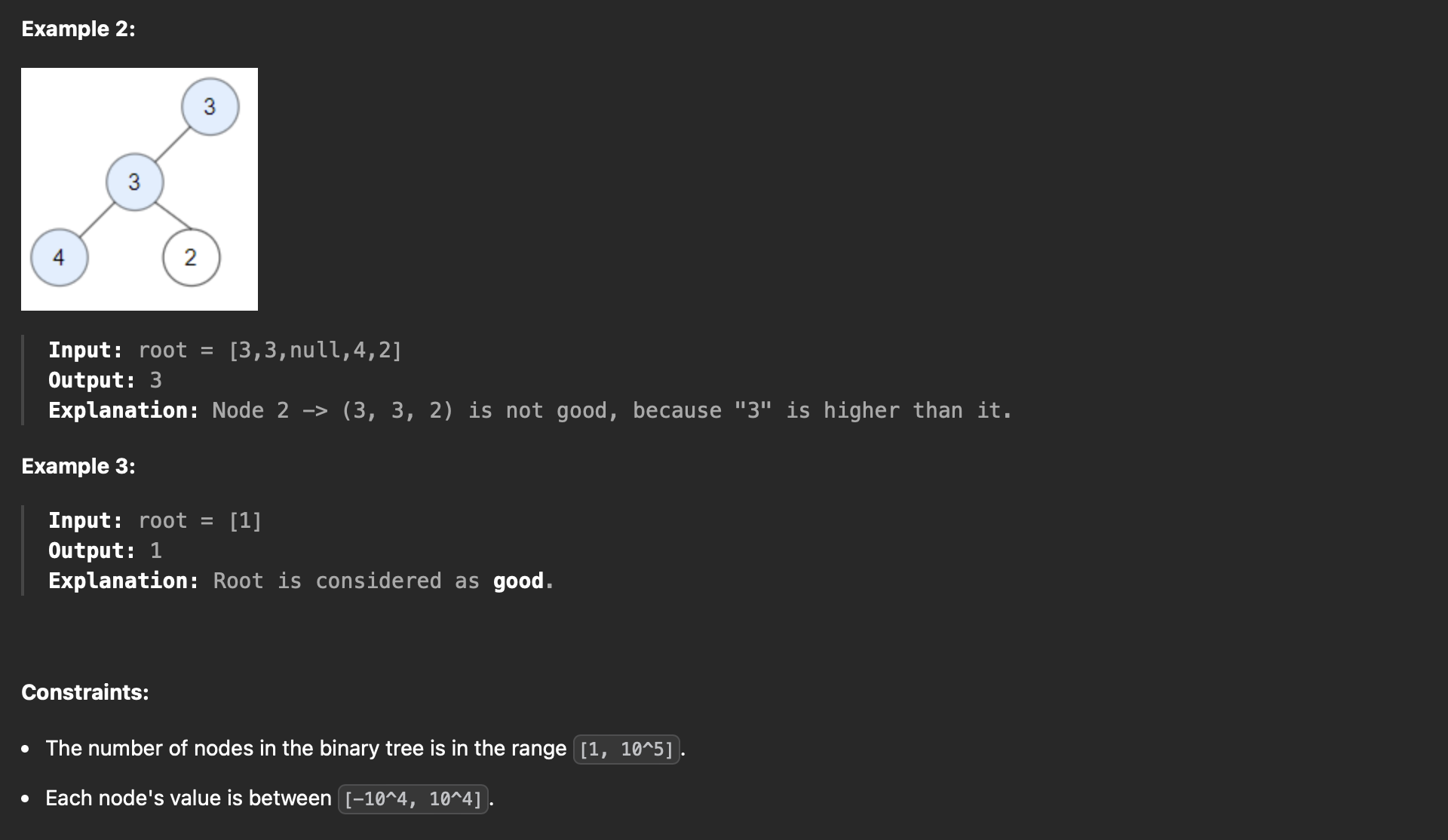
이진 트리가 주어지면, 루트노드에서 X 노드까지의 경로 에서 X 노드의 값보다 보다 큰 값을 가진 노드가 없다면 해당 노드 X는 'good' 으로 정의할 수 있다.
해당 이진 트리의 'good' 노드의 수를 반환 한다.
문제 풀이 방법
dfs로 루트 노드에서 X 노드 까지의 원소를 탐색하는데, 해당 X 노드 까지 탐색하는 과정에서 지나오는 노드의 값을 업데이트 해주고, 마지막 X 노드와의 값을 비교해서 good인지 아닌지에 대한 카운팅을 업데이트 한다.
내 코드
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def goodNodes(self, root: TreeNode) -> int:
def dfs(node, maxVal):
if not node:
return 0
ans = 1 if node.val >= maxVal else 0
maxVal = max(maxVal, node.val)
ans += dfs(node.left, maxVal)
ans += dfs(node.right, maxVal)
return ans
return dfs(root, root.val)
[11] 230. Kth Smallest Element in a BST
https://leetcode.com/problems/kth-smallest-element-in-a-bst/
문제 설명
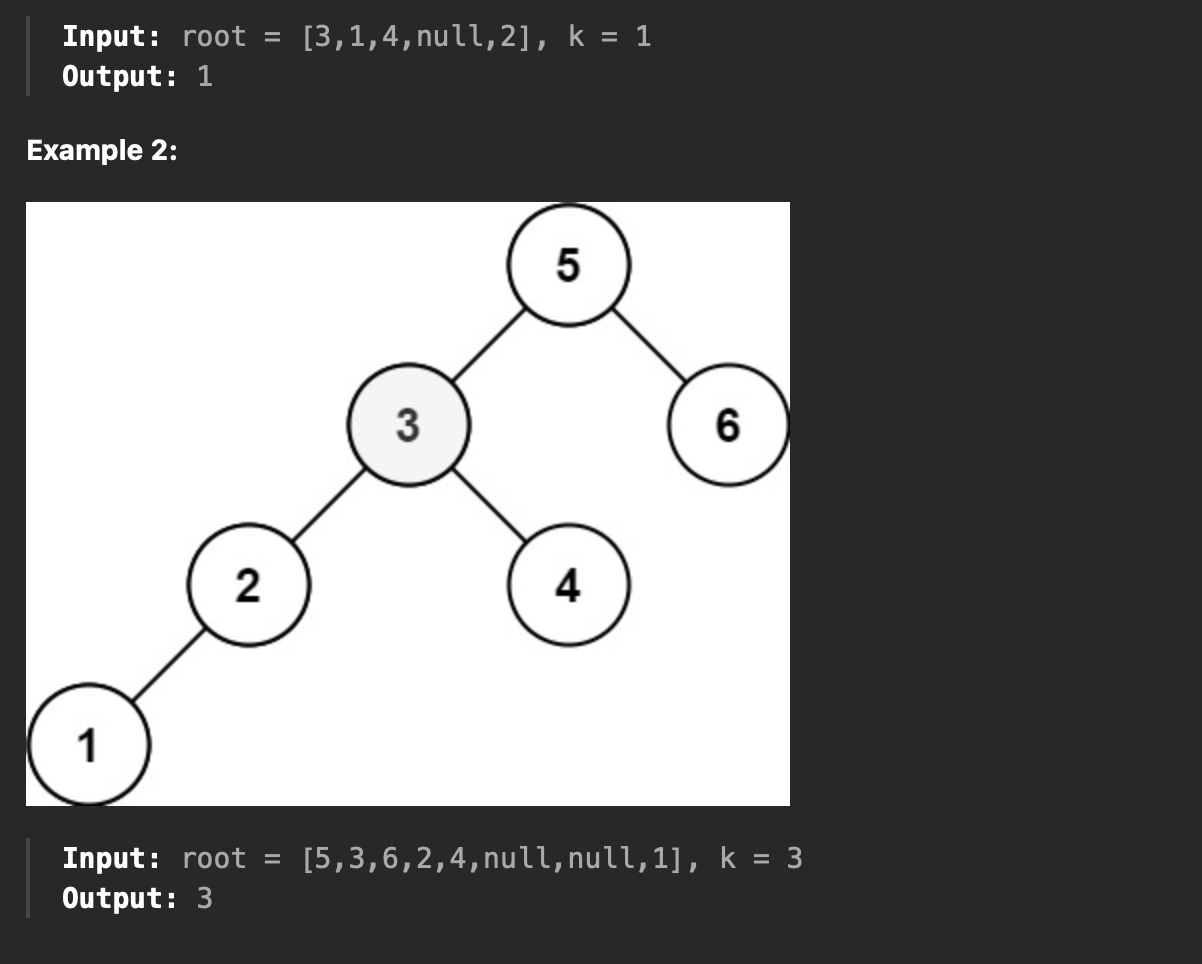
이진 트리가 주어 질때, 이진 트리의 원소중에서 k번째로 작은 노드를 리턴한다.
문제 풀이 방법
처음에는 그냥 전체 원소를 dfs로 돌면서 리스트에 원소를 담고, 리스트를 sort 한다음 k번째를 리턴했는데, 그럴 경우 시간복잡도가 O(nlogn), 공간복잡도가 O(n)이다.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:
ans = []
def dfs(node):
if not node:
return None
ans.append(node.val)
left, right = dfs(node.left), dfs(node.right)
dfs(root)
return sorted(ans)[k-1]
이를 최적화하기 위해서 해당 이진 트리들은 루트 노드 왼쪽은 무조건 작은 수가 위치한다는 것을 이용하면서 가장 최하단의 왼쪽 노드까지 갔다가 백트래킹하면서 올라오고, k번째 도달했을때 해당 원소를 리턴하면 시간복잡도 O(n), 공간복잡도 O(logN) 으로 해결할 수 있다.
내 코드
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:
stack = []
cur = root
while cur or stack:
while cur:
stack.append(cur)
cur = cur.left
cur = stack.pop()
k-=1
if k==0:
return cur.val
cur = cur.right
[12] 235. Lowest Common Ancestor of a Binary Search Tree
https://leetcode.com/problems/lowest-common-ancestor-of-a-binary-search-tree/
문제 설명

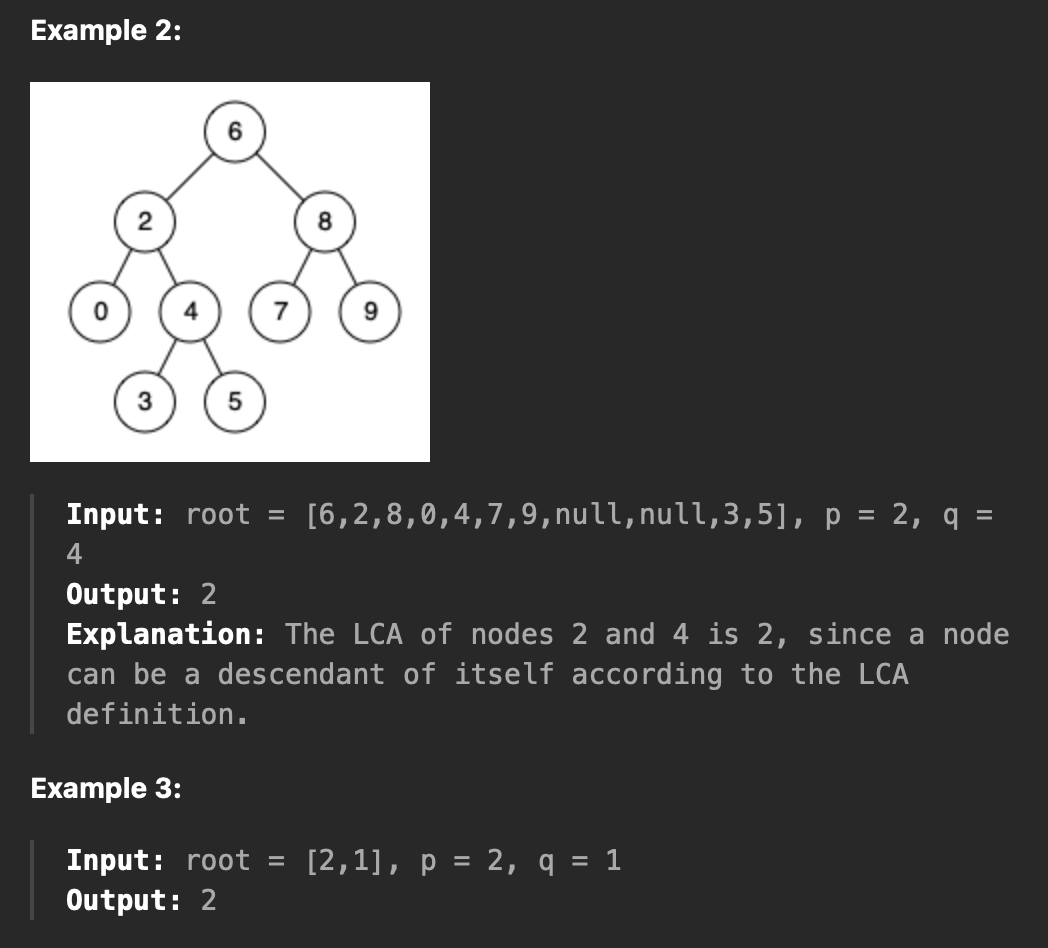
이진트리와 이진 트리의 노드의 원소가 주어질 때, 두 노드 중 가장 낮은 공통 조상(LCA) 노드를 찾는다.
Wikipedia의 LCA 정의는 “최하위 공통 조상은 두 노드 p와 q 사이에서 p와 q를 모두 자손으로 갖는 T의 가장 낮은 노드로 정의한다.(노드가 자체의 자손이 되도록 허용)”
문제 풀이 방법
이진트리는 왼쪽 노드가 조상 노드보다 크기가 작고, 오른쪽 노드가 조상 노드보다 크기가 크므로 이를 이용해서, 들어오는 왼쪽 노드와 오른쪽 노드의 값이 루트노드 보다 작으면 루트 노드는 왼쪽으로 이동하고, 왼쪽 노드와 오른쪽 노드가 루트 노드보다 크다면 루트 노드는 오른쪽으로 이동하면서 최하위 공통 조상을 찾아간다.
내 코드
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
while True:
if root.val < p.val and root.val < q.val:
root = root.right
elif root.val > p.val and root.val > q.val:
root = root.left
else:
return root
[13] 98. Validate Binary Search Tree
문제 설명
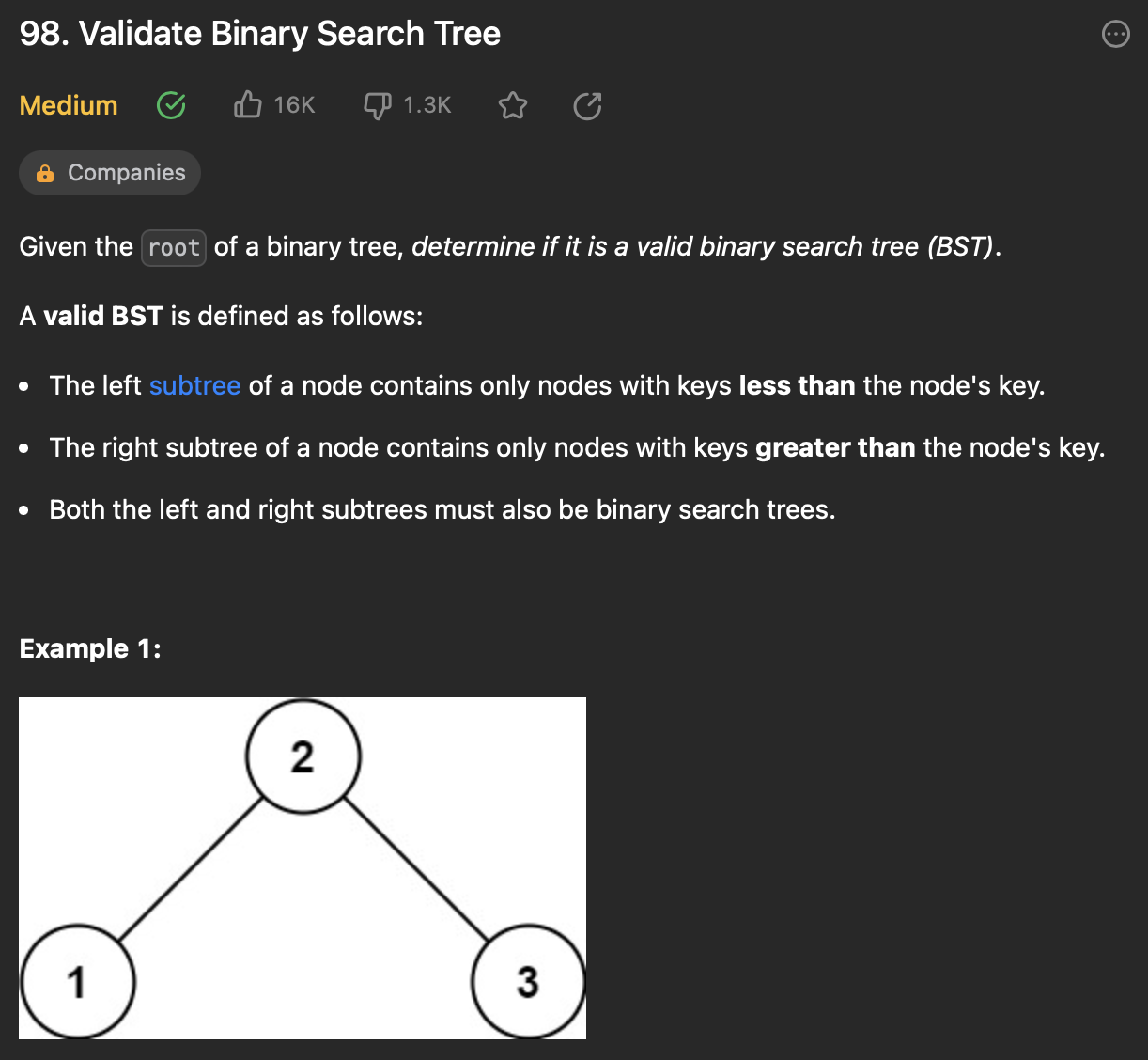
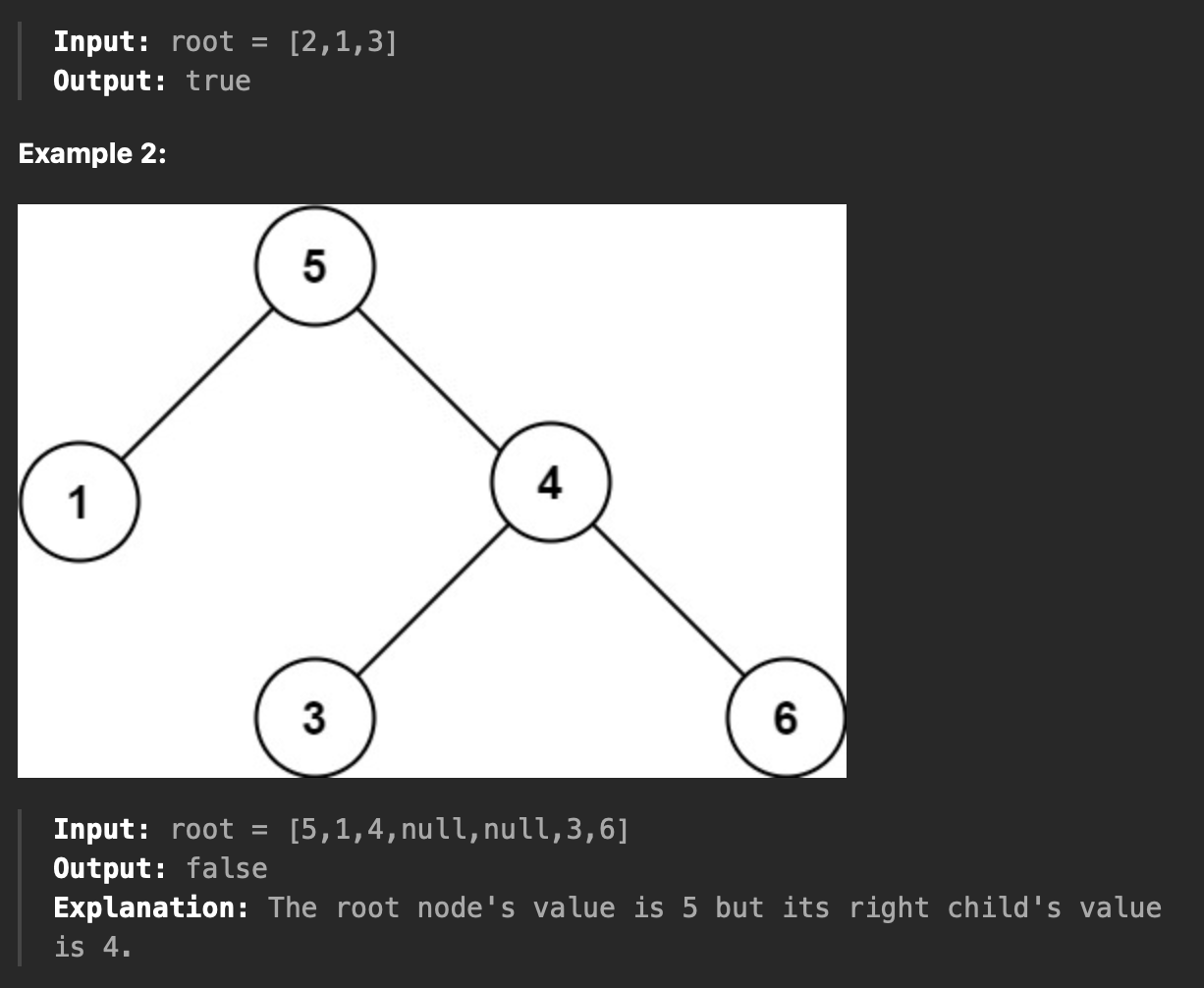

주어진 이진트리가 유효한 binary search Tree 형태를 갖추고 있는지 여부를 리턴한다.
조건은 루트노드의 왼쪽 자식 노드들은, 루트노드보다 작아야 하고 루트노드의 오른쪽 자식 노드들은 루트 노드보다 큰 값을 가지고 있어야 한다.
문제 풀이 방법
dfs 방식으로 순차적으로 내려가면서, 유효한 이진 트리이게끔 왼쪽 범위와 오른쪽 범위를 업데이트 해주면서, 해당 노드들이 범위에 들어오는지에 대한 유무를 판단해주면 된다.
첫 시작의 루트노드는 아주 작은 숫자보다크고 아주 큰 숫자보다 작은 float('-inf'), float('inf')로 시작 하는 것이 중요하다.
왼쪽 노드의 값은 바로 윗부모노드의 값보다 작아야하고, 오른쪽 노드의 값은 윗부모노드의 값보다 커야하므로 계속 해서 업데이트 한다.
내 코드
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isValidBST(self, root: Optional[TreeNode]) -> bool:
def valid(node, left, right):
if not node:
return True
if not (left < node.val < right):
return False
return valid(node.left, left, node.val) and valid(node.right, node.val, right)
return valid(root, float('-inf'), float('inf'))
여담
트리 하드 문제 2개는 trie와 함께 풀도록 하겠다!
알듯 말듯 재밌지만 빡도는 트리~!
트리를 이해해야지 그래프로 넘어가지
트리야 트리야 ~
