[Algorithm] Backtracking (백트래킹/퇴각검색)

gunny·2023년 5월 10일

Backtracking Algorithm algorithm 백트래킹 백트래킹 알고리즘 퇴각검색

Algorithm

목록 보기

2/7

Algorithm - Backtracking

(1) Backtracking Algorithm 정의

Backtracking(백트래킹/퇴각검색) : 해를 찾는 도중 해가 아니여서 막히면, 되돌아가서 다시 해를 찾는 기법. 최적화 문제와 결정 문제를 푸는 방법
DFS를 사용해서 조건에 맞지 않으면 중단하고, 이전으로 돌아가서 다시 확인하는 것을 반복하면서 원하는 값을 찾는 알고리즘
제약 조건 만족 문제(Constraint Satisfaction Problem)에서 해를 찾기 위한 전략

(2) Backtracking Algorithm 동작 방식

(2)-a. DFS(깊이 우선 탐색)과의 비교

DFS는 가능한 모든 경로(후보)를 탐색해서, 불필요한 경로를 사전에 차단하는 행위가 없어서 경우의 수를 줄이지 못함
그래서, N! 가지의 경우의 수를 가진 문제는 DFS로 처리가 불가능
백트래킹(Backtracking)의 경우, 해를 찾아가는 도중에 현재의 경로에서 해가 될 것 같지 않으면 경로를 가지 않고 되돌아옴
'가지 치기'로, 불필요한 경로를 조기에 차단할 수 있어 경우의 수가 줄지만, 만약 N! 의 경우의 수를 가진 문제에서 최악의 경우에는 여전히 지수함수의 시간을 필요로해 처리가 불가능 할 수 도 있어, '가지치기'를 얼마나 잘하느냐에 따라서 효율성이 결정됨

(2)-b. Backtracking의 동작 방식

모든 가능한 경우의 수 중에서 특정한 조건을 만족하는 경우만 살펴 보며,
답이 될 만한지 판다하고 그렇지 않으면 그 부분을 탐색하지 않고 가지치기를 함
DFS 등으로 모든 경우를 탐색하는 과정에서, 조건문을 걸어 답이 될 수 없는 상황을 정의해서 탐색을 중지시킨 후 이전으로 돌아가서 다른 경우를 탐색하도록 함
실제 구현 시 고려할 수 있는 모든 경우의 수 (후보군)을 상태공간트리(State space Tree) 를 통해 표현

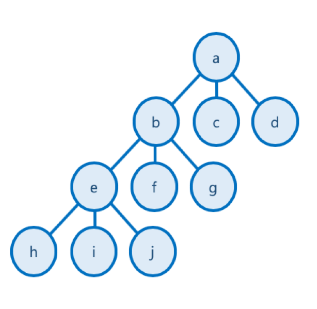<출처 : 잔재미코딩>

(2)-c. Backtraking의 유망성

어떤 노드의 유망성, 즉 해가 될 만한지 판단한 후 유망하지 않다고 결정되면, 그 노드의 이전(부모)로 돌아가(backtracking) 후, 다음 자식의 노드로 돌아감
해가 될 가능성이 있으면 유망하다(promising)고 하며, 유망하지 않은 노드에 가지 않는 것을 가지치기(pruning) 한다고 함

(3) Backtracking 구현

Backtracking은 'BFS'나 'DFS'와 함께 구현함
백트래킹 특성에서 조건에 부합하지 않으면(Node가 유망하지 않으면), 이전 노드로 돌아와야 하기 때문에 BFS 보다는 DFS 구현이 더 편함
실제 구현 시 고려할 수 있는 모든 경우의 수(후보군)을 상태공간트리(State Space Tree)를 통해 표현
Backtracking 구현 시 가장 중요한 것은 한정조건

(4) Backtracking 예시

3x3 행렬 선택 게임
{1,5,3}
{2,4,7}
{5,3,6}

와 같은 행렬이 존재할 때 3개의 숫자를 선택하는 게임으로,
단 선택한 숫자들의 행과 열은 모두 중복되면 안되며 가장 적은 점수를 얻는 것이 승리할 때 선택해야 하는 숫자 3개를 고르는 문제

=> 이 때, 이 문제를 푸는 방법은 모든 방법을 다해보는 것이지만,
조건으로 모두 '행'과 '열'이 달라야 한다는 것이고 이것이 바로 한정 조건 임
위에서 첫번째 행에서 만약 1을 택하면, 두 번째 행의 숫자는 2,4,7이 존재하지만 2는 1과 같은 열으로 더 탐색하더라도 정답이 될 수 없으므로 4,7만 유망하다.
이러한 방식으로 마지막 행까지 수행하면 트리 구조를 얻고, 결론적으로 정답을 찾아갈 수 있다.

import sys

li = [[1,5,3],[2,5,7],[5,3,5]]
chk = [False]*3
m = sys.maxsize

def backtracking(row, score):
	if row == 4: # 재귀함수를 마치는 조건
		if score < m:
			return
	for i in range(1,4):
		if chk[i] == false: # 백트래킹에서의 한정조건
			chk[i] = true
			backtracking(row+1, score + li[row][i])
			chk[i] = false
	return 

backtracking(1,0)
print(m)

N-Queen 문제
- N x N 크기의 체스판에 N개의 퀸을 서로 공격할 수 없도록 배치
- 퀸은 수직, 수평, 대각선 이동(공격) 가능
  즉, 한 행에는 하나의 퀸 밖에 위치할 수 밖에 없음(퀸은 수평 이동 가능)
- 맨 위의 행부터 퀸을 배치하고, 다음 행에 해당 퀸이 이동할 수 없는 위치를 찾아 퀸을 배치
- 만약, 앞선 행에 배치한 퀸으로 인해 다음 행에 해당 퀸이 이동할 수 없는 위치가 없을 경우 더이상 퀸을 배치하지 않고 이전 행의 퀸의 배치를 바꿈
- 맨 위의 행부터 전체 행까지 퀸의 배치가 가능한 경우의 수를 상태 공간 트리 형태로 만든 후, 각 경우를 맨 위의 행부터 DFS 방식으로 접근하고, 한정 조건이 발생할 경우 진행하지 않고 다른 경우를 탐색함
< 유망한(Promising) N-Queen 찾기>
- 한 행에 하나의 퀸만 배치 가능하므로, 수평 체크는 별도로 필요하지 않음