Bayes Error (베이즈 오류/에러)
1. Bayes Error 정의
- 베이즈 오류/에러는 달성할 수 있는 가장 낮은 예측 오차로, 감소 불가능한 오류이다.
- Traning data를 완벽히 학습하였을 때 (그 사건의 underlying density function[확률 분포]을 알고 있을 때), 그 Traning data에 대해 가장 확률이 높은 Class Label을 선택하는 방법에서 발생하는 이론적 최소 오차
- classification task에서 P(Y|X)에 대한 확률 분포(underlying true distribution)을 알고 있다고 가정할 때, 이론적으로 도달할 수 있는 최소의 classification error를 의미함
2. Bayes Error 의미
-
총 오차 = 베이즈 오차 + 모델이 베이즈 오차보다 얼마나 나쁜지이며 즉, 총 오차는 bias(편향) + variance(분산) + 환원 불가능한 오류의 합이라고 볼 수 있다.
-
베이즈 오류는 모델에 따라 달라질 수 있고 noise 분포의 고유한 특성이다.
-
여기서 중요한 것은, 확률 분포(underlyhing true distribution)을 알고 있어도 이를 통해 class label을 inference 하는 방법이 반드시 P(y1, x), P(y2, x)를 비교해서 확률이 높은 쪽을 정답으로 골라야만 이 Bayes Error에 도달 할 수 있다.
-
이 방식이 아닌 inference는 이론적으로는 Bayes error가 될 수 없는데, 확률 분포(underlying true distribution)가 알려진 상황에서는 optimal한 inference한 방법은 이론적으로 이미 밝혀졌다라고 할 수 있다.
-
즉, 우리가 풀어야 하는 문제는 확률분포(underlying true distribution)에 가장 근접한 분포를 기계학습으로 구하는 것이고, 이를 통해 class label을 inference하는 방법은 이미 정해져 있는 것임
3. Bayes Error 수식
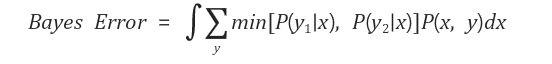
-
min[P(y1|x), P(y2|x)] : 확률이 가장 큰 y를 선택했을 때 발생하는 오차 값
-
P(x,y) : x와 y의 결합 확률(joint probability)
x와 y가 동시에 일어날 확률로, x,y 사건이 일어날 확률
=> 이 때 y는 summation rule에 의해 시그마가 사라지고 P(x)로 바뀜 -
bayes error는 오차값 *확률=오차의 평균을 계산한 것
4. Bayes Error 예
-
예를 들어, 동전을 던질 때 우리가 어떤 프로세스로 결과를 생성하는지 정확히 알고 있지만(이항 분포),
동전 던지기 결과를 예측하는 경우 프로세스가 본질적으로 무작위(확률적) 이기 때문에 오류를 범할 수 있다. -
어떤 동전에 실험을 통해 앞면과 뒷면이 4:1 확률로 나타냄을 알아냈는데
P(Head)= 0.75, P(Tail) = 0.25, 여기서 앞면을 1로 뒷면을 2로 정의 했을 때,동전을 한 번 던져 나오는 면을 예측하면 앞면이 나올 확률이 항상 높기 때문에 동전을 던지면 무조건 앞면으로 예측한다.
이때 발생하는 에러는 (앞이라고 예측했지만 뒷면이 나올때의 에러)는 Bayes error = (0.25)*1 = 0.25 이다.
-
여기서 1을 곱해주는 이유는 항상 p(x)가 일어나기 때문이고, 만약 동전을 50%의 확률로 던지면
Bayes error = (0.25)*0.5 = 0.125가 된다.
