[Tensorflow] 4. Sequences, Time Series and Prediction(2. Deep Neural Networks for Time Series) : lecture

[Tensorflow] 4. Sequences, Time Series and Prediction (2. Deep Neural Networks for Time Series)

시계열과 추세와 계절성과 같은 시계열의 일반적인 속성 알아보고, 예측을 위한 통계적 방법을 사용해본다.
딥러닝 신경망을 이용해 시계열 데이터를 인식하고 예측하도록 학습시킨다.

• 2추차에서는 시계열 데이터와 예측 모델에 대해 다루게 된다. 시계열 데이터는 시간에 따라 변화하는 데이터를 의미하며, 예를 들어 주식 가격, 기온 변화, 판매량 등이 시계열 데이터이다.
• 이 강의에서는 시계열 데이터를 분석하고 예측하기 위해 다양한 기법과 모델을 배운다.
• 딥러닝을 활용하여 시계열 데이터를 예측하는 방법에 대해 배우는데, 이를 통해 실제 데이터에 대한 예측 모델을 구축하는 능력을 향상시킨다.
• 이 강의는 DeepLearning.AI와 함께 제공되며, 실습과 과제를 통해 실제 데이터를 사용하여 모델을 구현하고 평가한다.

---

들어가기 앞서 1주차에서는 추세, 계절성, 노이즈를 포함한 합성 계절성 데이터 셋을 통계적 방법을 통해 알아봤다.
이번 장은 'machien learning'을 통해서 알아본다.

머신러닝을 학습하고, 이를 위해 통계 공부를 하다보면 자주 보는 질문이 있다. "머신러닝과 통계적 방법의 차이는 무엇인가?"

그것에 대해서는 이렇게 정리했다.

https://velog.io/@heyggun/%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D%EA%B3%BC-%ED%86%B5%EA%B3%84%EC%A0%81-%EB%B0%A9%EB%B2%95%EC%9D%98-%EC%B0%A8%EC%9D%B4

시계열 데이터를 분석하고 예측하는 두 가지 주요 접근 방식인 (a) 통계적 방법과 (b) 머신러닝 방법에 대해 각각 관점에서 살펴보자면

(a) 통계적 방법은 과거 데이터의 패턴과 통계적 속성을 분석해 미래 값을 예측 하는 방법으로 시계열 데이터의 특성을 먼저 이해한다.
시간에 따른 추세(trend), 주기성(seasonality), 잡음(noise)등을 고려한다.
주로 평균, 분산, 자기상관 등의 통계적 지표를 사용해서 데이터의 특성을 파악하고 예측 모델을 구축한다. 예를 들어 이동평균법, 지수평활법, ARIMA 등의 통계적 모델을 사용해 시계열 데이터를 예측할 수 있다.

(b) 머신러닝 방법은 데이터에서 패턴을 학습하고 예측하는 방법이다. 시계열 데이터를 입력으로 사용하여 모델을 학습시키고, 새로운 데이터에 대한 예측을 수행한다.
주로 신경망 모델인 딥러닝을 사용하여 시계열 데이터를 예측한다.
예를 들어, 순환 신경망(RNN)이나 장기 단기 기억 네트워크(LSTM)와 같은 모델을 사용하여 시계열 데이터의 패턴을 학습하고 예측한다.

정리하자면 통계적 방법은 데이터의 통계적 특성을 활용하여 예측을 수행하는 반면, 머신러닝 방법은 데이터의 복잡한 패턴을 학습하여 예측을 수행한다.
어떤 방법을 선택할지는 데이터의 특성과 예측의 목적에 따라 다를 수 있다.
이 강의에서는 머신러닝 방법을 사용하여 시계열 데이터를 예측하는 방법을 다루고 있다.

[1] Preparing features and lables

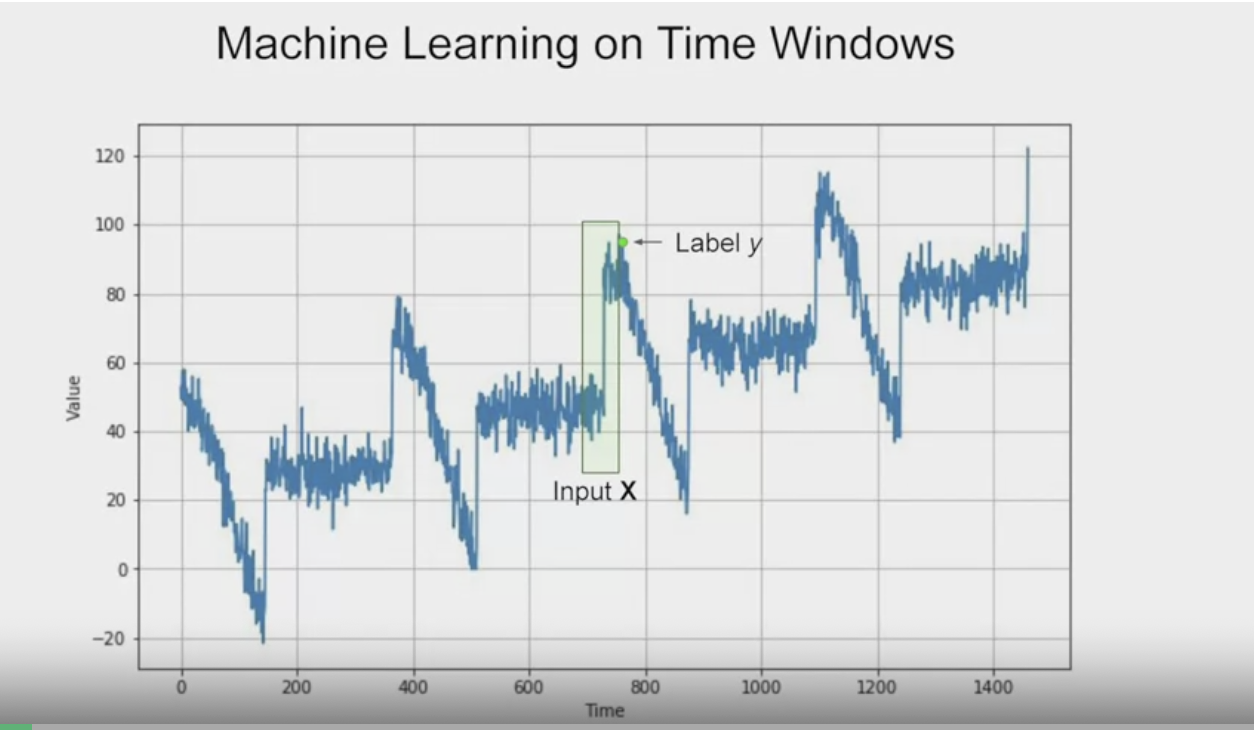
시계열 데이터 역시 다른 머신러닝 문제와 마찬가지로 데이터를 feature와 label로 분류해야 한다. feature는 시계열의 값 수이이고 label은 다음 값이 된다.
값의 수는 feature로 하고 window size는 데이터의 크기이고 머신러닝 모델을 훈련한다.
예를 들어 시계열 데이터에서 한번에 30일을 다룬다면 30개의 feature로 해서 다음 값을 label로 인식하는 것이다.
그리고 신경망을 훈련해서 단일 레이블에 30개의 feature를 매칭한다.

아래에 데이터를 생성하고 값의 범위를 10개로 지정하면 다음과 같은 output을 볼 수 있다.

dataset = tf.data.Dataset.range(10)
for val in dataset:
	print(val.numpy()
   
 # output
 1
 2
 3
 4
 5
 6
 7
 8
 9

dataset window를 통해 창으로 데이터 세트를 확장해본다.
parameter는 window의 크기 이고 매회 shift하는 양이다.
아래에서는 widnow size를 5로 shift를 1로 설정했다.

dataset = tf.data.Dataset.range(10)
dataset = dataset.window(5, shift=1)
for window_dataset in dataset:
	for val in window_dataset:
    	print(val.numpy(), end=" ")
    print()
    
# output
0 1 2 3 4
1 2 3 4 5
2 3 4 5 6
3 4 5 6 7
4 5 6 7 8
5 6 7 8 9
6 7 8 9
7 8 9
8 9 
9

위에서 window를 5로 지정했기 때문에 한 row당 1~9까지의 숫자 중 5개가 찍히는
0,1,2,3,4가 찍히고 다음으로 shift=1을 했기 때문에 다음 줄은 1,2,3,4,5 가 나온다.
데이터 세트의 끝에 가면 값의 수가 적어지는데 다음 값이 존재하지 않기 때문이다.

이제 창을 조금 조절해서 균일한 크기의 데이터를 도출해보자.
drop_remainer 를 true로 하면 남은 값을 모두 탈락시켜 데이터를 다듬어 준다.
즉 5개의 항목이 표시되는 창만 보여준다.

dataset = tf.data.Dataset.range(10)
dataset = dataset.window(5, shift=1, drop_remainder=True)
for window_dataset in dataset:
	for val in window_dataset:
    	print(val.numpy(), end=' ')
    print()
    
# ouput 
0 1 2 3 4
1 2 3 4 5
2 3 4 5 6
3 4 5 6 7
4 5 6 7 8
5 6 7 8 9

이들 값을 numpy로 넣어서 머신러닝에 활용해보자.
데이터 세트의 각 항목에 대해 numpy 메서드를 호출해서 프린트해본다.

dataset = tf.data.Dataset.range(10)
dataset = dataset.window(5, shift=1, drop_reminder=True)
dataset = dataset.flat_map(lambda window : window.batch(5))
for window in dataset:
	print(window.numpy())
    
#output
[0 1 2 3 4]
[1 2 3 4 5]
[2 3 4 5 6]
[3 4 5 6 7]
[4 5 6 7 8]
[5 6 7 8 9]

다음으로 데이터를 feature와 label로 분할해본다.
목록의 각 항목에 대해 마지막 값을 제외한 모든 값을 활용하고 나머지는 label이다.
이는 매핑을 이용해서 마지막을 제외한 모든 값은 :-1로, 마지막만 -1:로 분할한다.

dataset = tf.data.Dataset.range(10)
dataset = dataset.window(5, shift=1, drop_remainder=True)
dataset = dataset.flat_map(lambda window : window.batch(5))
dataset = dataset.map(labmda window : (window[:-1], window[-1]))
for x,y in dataset:
	print(x.numpy(), y.numpy())
#output
[0 1 2 3] [4]
[1 2 3 4] [5]
[2 3 4 5] [6]
[3 4 5 6] [7]
[4 5 6 7] [8]
[5 6 7 8] [9]

일반적으로는 훈련 전에 데이터를 섞어 둔다.
shuffle 메서드를 사용한다.

dataset = tf.data.Dataset.range(10)
dataset = dataset.window(5, shift=1, drop_remainder=True)
dataset = dataset.flat_map(lambda window : window.batch(5))
dataset = dataset.map(labmda window : (window[:-1], window[-1]))
dataset = dataset.shuffle(buffer_size=10)
for x,y in dataset:
	print(x.numpy(), y.numpy())
    
# output
[3 4 5 6] [7]
[4 5 6 7] [8]
[1 2 3 4] [5]
[2 3 4 5] [6]
[5 6 7 8] [9]
[0 1 2 3] [4]

마지막으로 데이터 일괄처리는 배치 메서드로 가능하다.

dataset = tf.data.Dataset.range(10)
dataset = dataset.window(5, shift=1, drop_remainer=True)
dataset = dataset.flat_map(lambda window : window.batch(5))
dataset = dataset.map(lambda window : (window[:-1], window[-1]))
dataset = dataset.shuffle(buffer_size=10)
# 사이즈 parameter 2 : 데이터를 2개의 세트로 일괄처리
dataset = dataset.batch(2).prefetch(1)
for x, y in dataset:
	print('x = ', x.numpy())
    print('y = ', y.numpy())
    
 # output 
 # 각 2개의 데이터 항목이 포함된 3개의 배치가 있음
 x = [[4 5 6 7] [1 2 3 4]]
 y = [[8] [5]]
 x = [[3 4 5 6] [2 3 4 5]]
 y = [[7] [6]]
 x = [[5 6 7 8] [0 1 2 3]]
 y = [[9], [4]]

[2] Preparing featrues and labels(screencast)

[1]에서 했던 것을 jupyter notebook으로 수행한다.

[3] Feeding windowed dataset into neural network (신경망에 윈도우 데이터 세트 넣기)

위에서는 dataset에서 window를 생성해서 머신러닝을 위한 시계열 데이터를 준비했다.
이전의 n값은 입력값인 feature 또는 x가 되고, 시간 단계상의 현재값은 출력값인 레이블 또는 y가 된다.

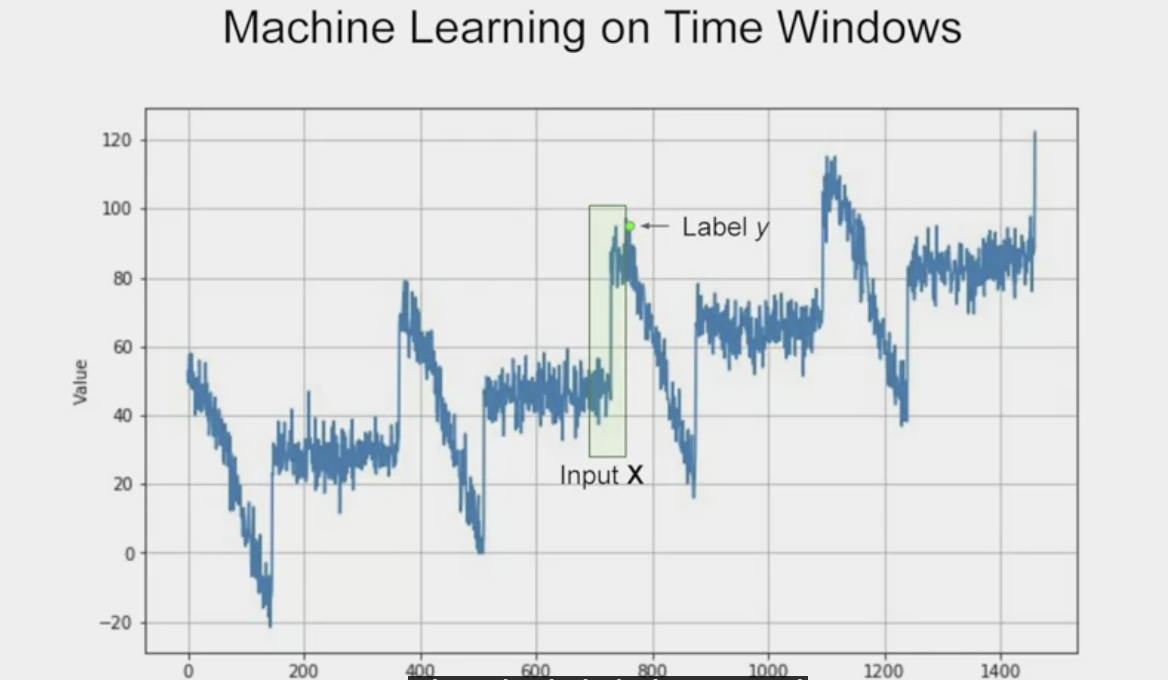
다수의 입력값인 x는 통상 data의 window로 불린다.
tensorflow dataset으로 해당 window를 생성할 수 있다.

원하는 window 크기에 대한 파라미터에 따라 데이터 시리즈를 처리하는 window_dataset 함수이다. 훈련시 사용하는 배치의 크기와 데이터가 섞이는 방식을 결정하는 shuffle_buffer도 있다.

def windowed_dataset(series, window_size, batch_size, suffle_buffer):
	dataset = tf.data.Dataset.from_tensor_slices(series)
    dataset = dataset.winodw(window_size+1, shift=1, drop_remainder=True)
    dataset = dataset.flat_map(lambda window : window.batch(window_size+1))
    dataset = dataset.shuffle(shuffle_buffer).map(lambda window : (window[:-1], window[-1]))
    dataset = dataset.batch(batch_size).prefetch(1)
  	return dataset

• tf.data.Dataset으로 시리즈에서 데이터 세트를 생성한다.
  from_tensor_slices 함수를 통과시킨다.
• dataset에서 window 메서드를 사용해서 winodw_size를 기준으로 데이터를 분할한다. 각각 1개의 시간 단위로 shift 하고, drop_remainder를 True로 해서 크기를 동일하게 유지한다.
• 쉽게 작업할 수 있도록 window_size +1 로 병합하고, 병합한 후에 shuffle로 병합한다. shuffle_buffer 를 설정하면 속도가 조금 더 빨라진다.
  예를 들어 데이터 세트에 10만개의 항목이 있고, 버퍼를 1,000으로 설정하면 1,000개의 요소 중 무작위로 선택한 하나로 첫 번째 버퍼를 채우고 이를 1,000개와 첫 번째 요소로 대체하고 다시 무작위로 선택하는 식이다. 거대 규모의 데이터 세트라도 더 작은 수치 중에 무작위로 선택하는 방식으로 속도를 높힐 수 있다.
• 섞인 데이터는 x로 분할되고, x는 마지막을 제외한 모든 요소이고 마지막 요소는 y이다.
• 선택한 배치크기로 일괄 처리 및 반환된다.

[4] single layer neural network (단일 계층 신경망)

데이터 세트를 window로 적용했으니, 신경망을 이용해본다.
아주 간단한 선형 회귀를 통해서 정확도를 측정하고 이를 개선해본다.
훈련을 시작하기 전에 데이터세트를 훈련 세트와 검증세트로 나눈다.

시간 단계를 1,000으로 수행하는 코드이다.
훈련 데이터는 x_train이라는 시리즈의 split_time에 대한 서브세트이다.

split_time =1000
time_train = time[:split_time]
x_train = series[:split_time]
time_valid = time[split_time:]
x_valid = series[split_time:]

간단한 선형 회귀 코드이다.

window_size = 20
batch_size =32
shuffle_buffer_size = 1000

dataset = windowed_dataset(series, window_size, batch_size, shuffle_buffer_size)
l0 = tf.keras.layers.Dense(1, input_shpae([window_size])
model = tf.keras.models.Sequential([l0])

• windowed_dataset 함수에 통과시킬 모든 함수를 설정한다.
  데이터의 window_size, 훈련을 위한 batch_size, shuffle_buffer_size이다.
• windows_dataset을 통과시켜 훈련을 위해 활용할 수 있는 형태가 마련된다.
• 다음으로 단일 Dense 레이어를 만들어 input_shape를 window_size 로 한다.
• 레이어를 l0라는 변수에 통과시켜 나중에 학습 가중치를 프린트할 때, 레이어를 참고하는 변수하고 있으면 쉽게 수행이 가능하다.
• 다음으로는 단일 레이어를 포함하는 시퀀스 모델을 정의한다.

model.compile(loss='mse', optimizer=tf.keras.optimizers.SGD(learning_rate=1e-6, momentum=0.9))
model.fit(dataset, epochs=100, verbose=0)

• loss를 mse로 평균제곱오차 손실함수를 설정, 옵티마이저로 확률적 경사하강법을 사용한다. 파라미터를 momentum을 사용했다.
• verbose=0으로 설정하면 epoch 출력을 제외한 epoch는 무시하게 된다.

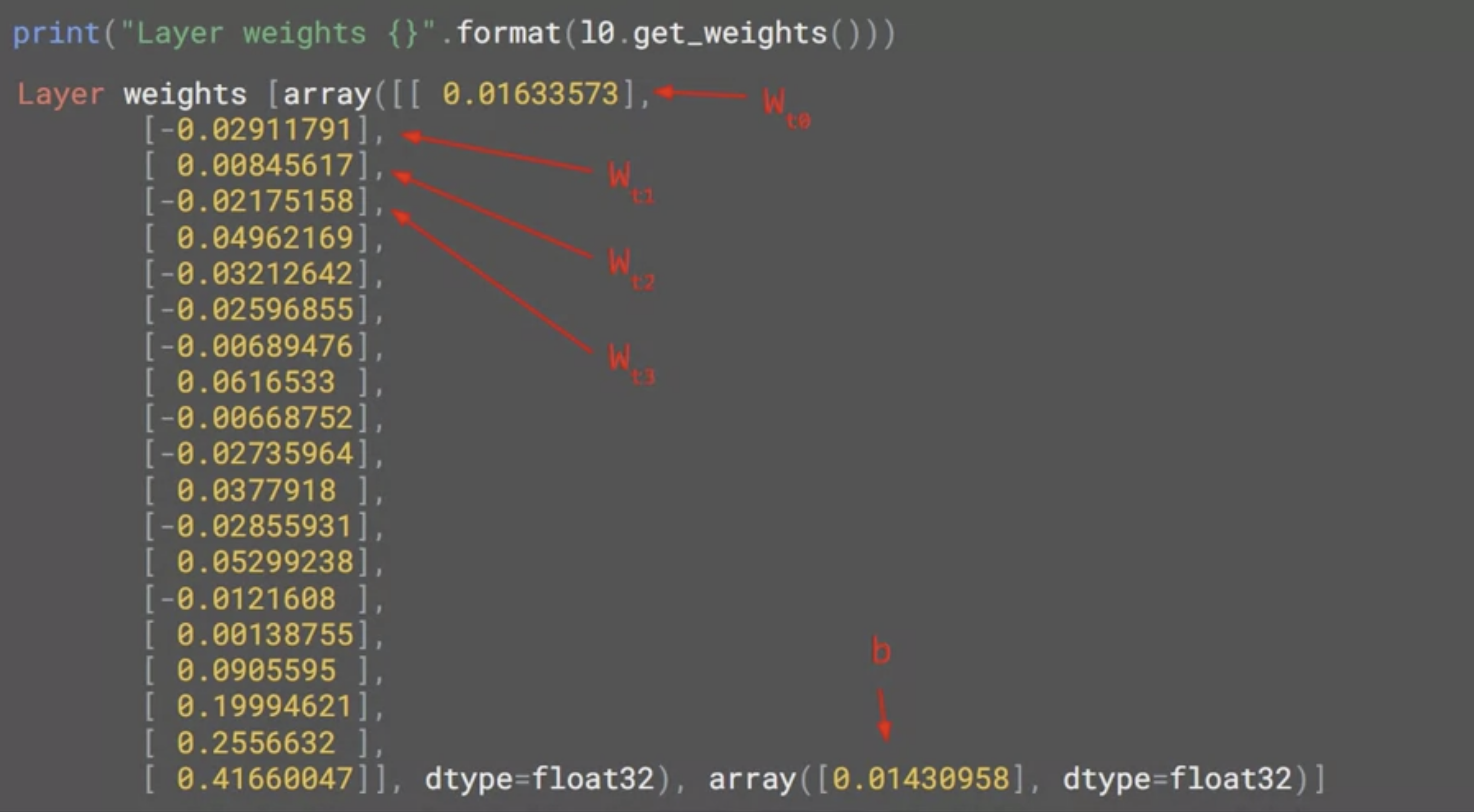
l0 라는 이름의 변수로 레이어를 참조했기 때문에 출력의 값은
첫번 째 배열에 20개의 값, 두 번째는 1개의 값이 있다.

• 네트워크가 선형 회귀를 학습하여 최대한 적합한 값을 찾아냈기 때문이다.
  첫 번째 열에 있는 각각의 값은 x의 20개 값에 대한 가중치이고 두 번째 배열의 값은 b 값으로 본다.

[5] Machine learning on time windows

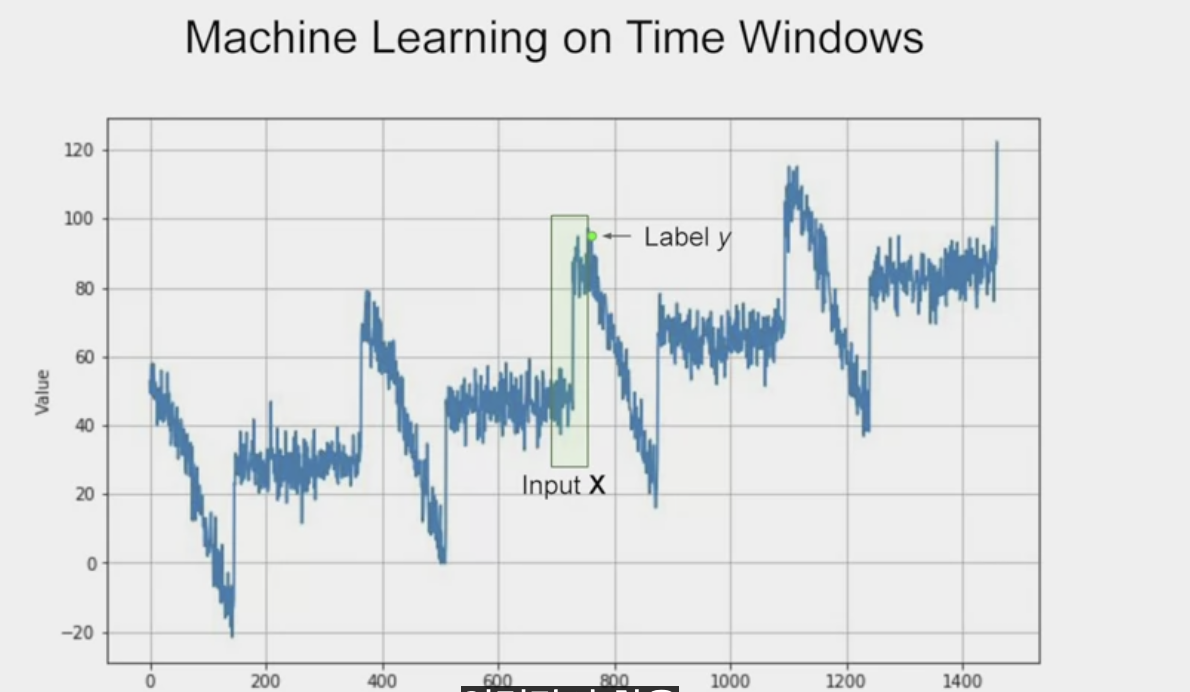
위 그림에서 입력창의 window를 20개의 값이라고 보고 각각을 x0, x1 .. x19까지 가보자.
여기서 통상 x축이라고 불리는 것은 가로축의 값이 아니다. 가로축 한 지점의 시계열 값에 해당한다.
즉, 현재값으로부터 20단계 이전에 있는 시간의 t0의 값을 x0이라고 한다. t1은 x1이다.
마찬가지로 출력의 값은 현재의 값을 y라고 한다.

[6] Prediction

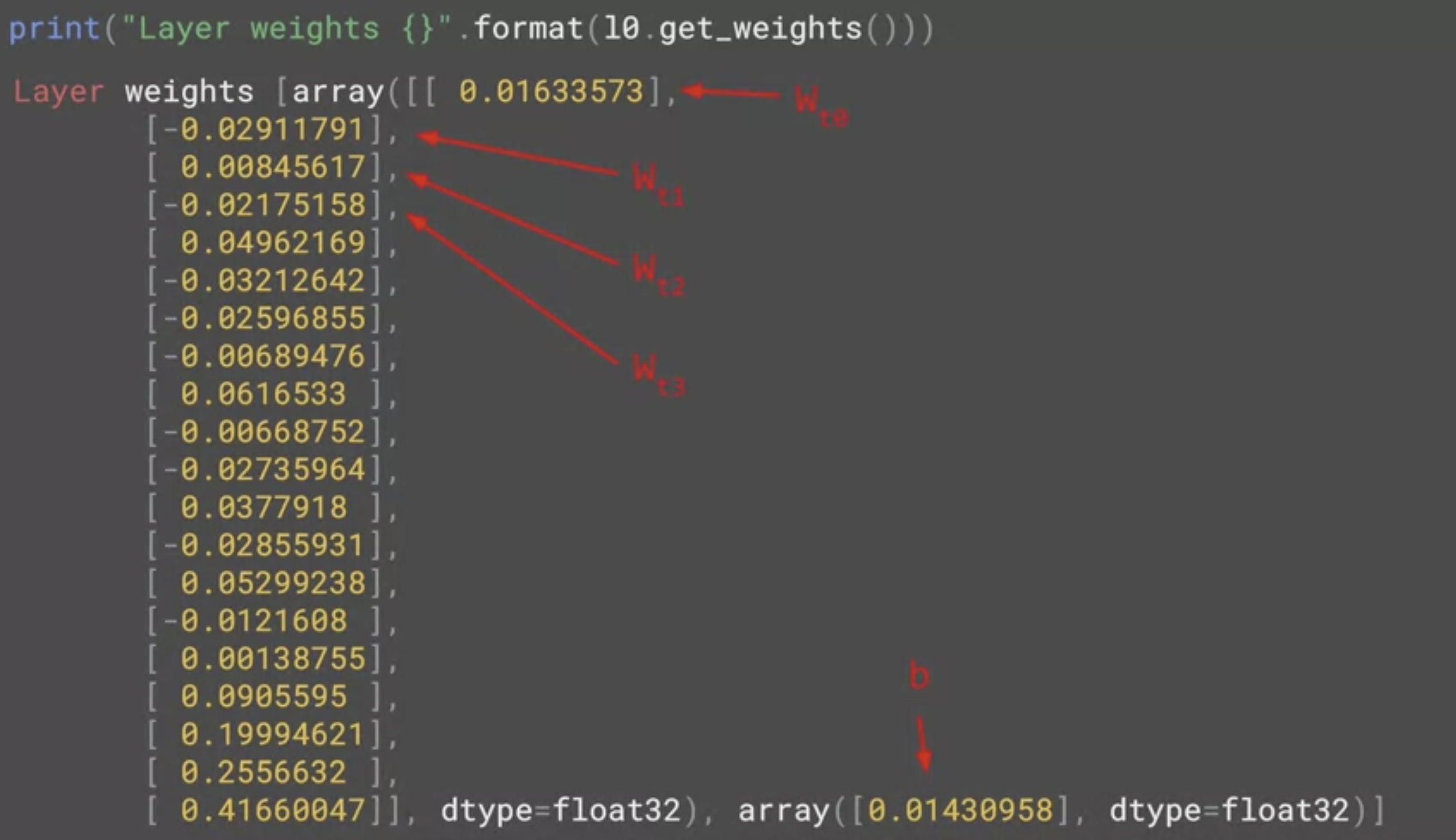
값을 살펴보면 b는 편향이고, 나머지는

이들이 특정 시간 단계의 값에 대한 가중치라는 것을 확인할 수 있다.
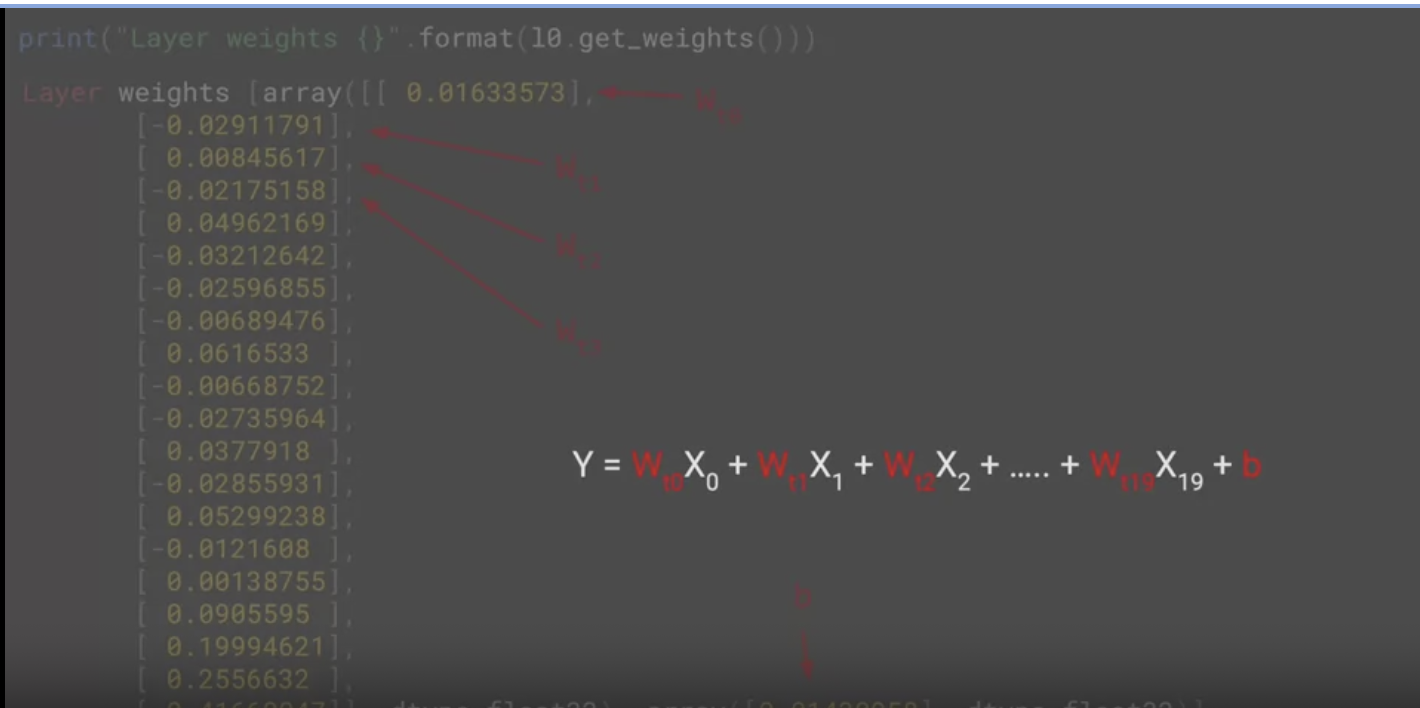
이와 같은 일반 선형회귀로 y 값을 예측해 볼 수 있다.
어느 단계에서든 x값에 가중치를 곱한 다음 편향을 더한다.

print(series[1:21])
model.predict(series[1:21][np.newaxis])

예를 들어서 시리즈에서 20개 항목을 프린트하면 20x 값이 나오고,
이 값을 예측하고 싶다면 해당 시리즈를 모델에 통과시켜 모델이 예측하도록 한다.

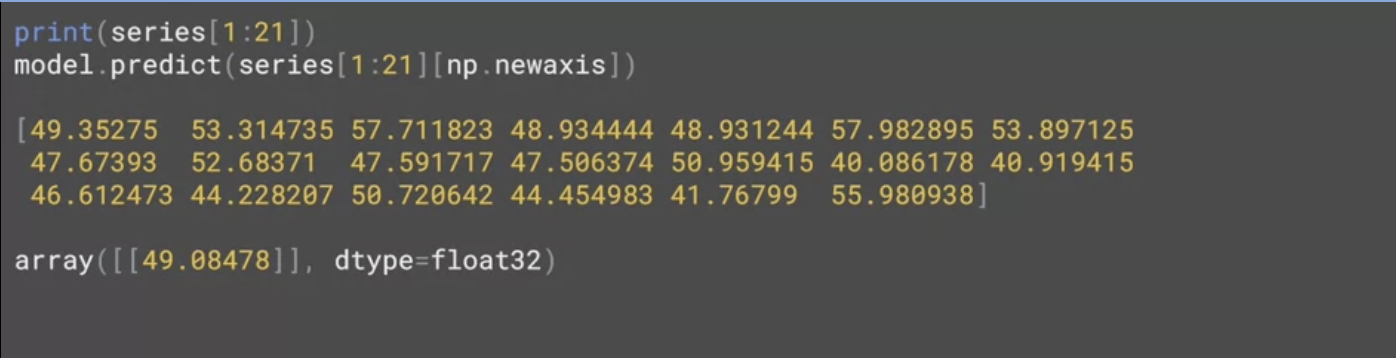
상단에 있는 20개의 값은 모델에 입력값을 제공하고 하단은 모델에서 반환 받은 예측값이다.
이처럼 20개의 값이 주어지면 49.08478을 다음 값으로 예측하는 것이다.

forecast = []
for time in range(len(series) - window_size):
	forecast.append(model.predict(series[time:time+window_size][np.newaxis]))

forcast = forecast(split_time-window_size:]
results = np.array(forecast)[:, 0, 0]

• 창 크기가 20일때 시계열의 모든 시리즈에서 20포인트 앞선 지점에 대해 예측값을 플로팅하고 싶다면 위와 같은 코딩을 진행한다.
  예측값의 빈 목록을 생성하고 시리즈를 반복해서 실행해서 예측한 다음에 결과값을 추가한다.
  시계열을 훈련과 테스트로 분류해서 특정 시점 이전은 훈련으로 사용하고 나머지는 검증으로 사용한다.
  분할된 시간 이후를 예측하고 numpy로 배열을 불러와 차트를 만든다.

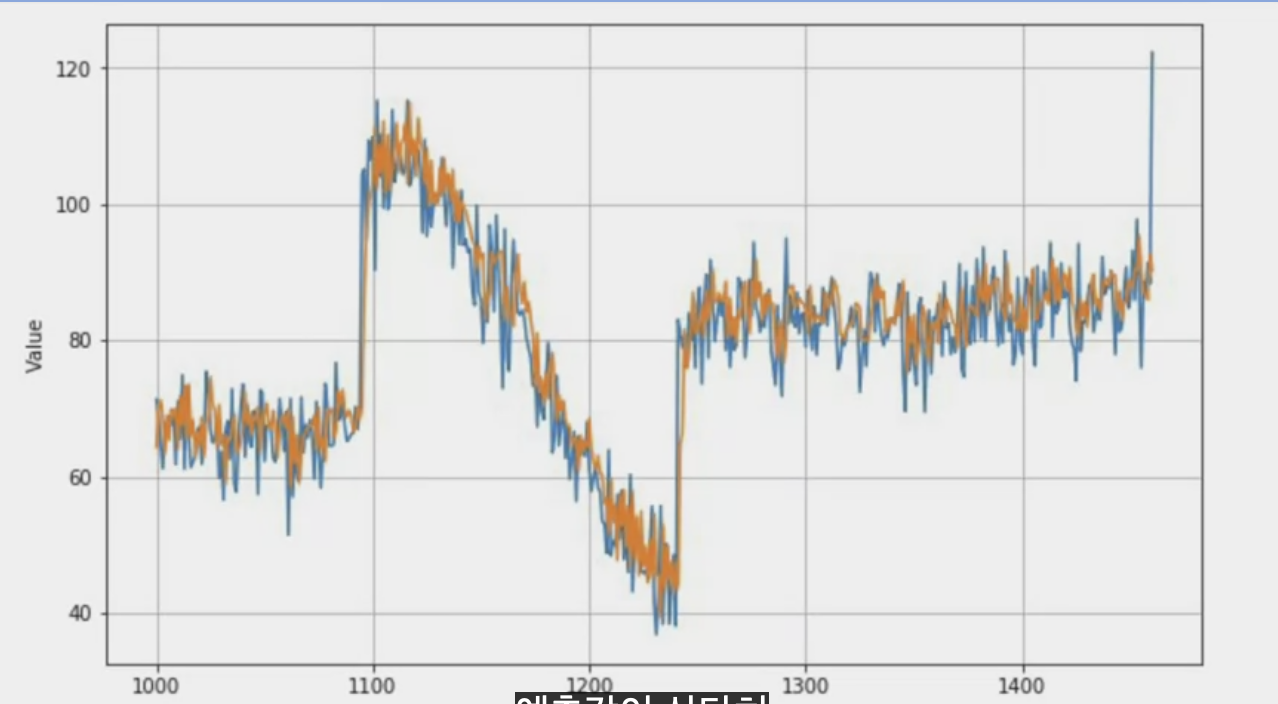
실제값은 파란색, 예측값은 주황색이다.

그 이후에 평균절대오차를 구해본다.

tf.keras.metrics.mean_absolute_error(x_valid, results).numpy()

#4.9526777

위의 과정은 신경망의 단일 레이어로 선형 회귀를 계산한 결과이다.

[7] More on single layer neural network

데이터 시리즈를 생성하고 헬퍼함수를 사용해, 시계열 데이터를 훈련 및 검증 데이터로 분리하는 notebook을 수행한다.
프로그래밍 과제는 다른 포스팅에서 더 자세하게 풀어서 작성할 생각이다.

[8] Deep neural network training, tuning and prediction

위에서는 데이터를 window로 나누어서 간단한 단일 레이어 신경망으로 선형 회귀로 재현했다.
이제는 DNN을 활용해서 모델의 정확도를 개선해본다.

dataset = windowed_dataset(x_train, window_size, batch_size, shuffle_buffer_size)
model = tf.keras.models.Sequential([
tf.keras.layers.Dense(10, input_shpae=[window_size], activation='relu'),
tf.keras.layers.Dense(10, activation='relu'),
tf.keras.layers.Dense(1)
])
model.compile(loss='mse', optimizer=tf.keras.optimizers.SGD(learning_rate=1e-6, momentum-0.9))
model.fit(dataset, epoches=100, verbose=0)

• 3개의 레이어가 있는 심층 신경망이다.
  먼저 데이터 세트를 생성하고 x_train 데이터와 window_size, batch_size, shuffle_buffer_size 를 결정한다.
• 10개, 10개, 1개의 뉴런을 지닌 3개의 레이어로 모델을 구성한다. input_shpae는 window의 크기이고, 각 레이어는 ReLU로 활성화한다.
  이전처럼 평균제곱오차 손실함수로 컴파일하고 옵티마이저로 확률적 경사하강법을 사용한다.
  모델을 100epochs로 훈련한다.

평균절대오차를 계산해보면 이전보다 작기 때문에 제대로 된 방향으로 학습하고 있다.
그러나 이러한 방법도 추측값이다.

우리가 선택한 학습률이 아니라 최적의 학습률을 선택할 수 있다면 더 나은 결과가 나올 수 있다. 더 효율적으로 학습해 더 나은 모델을 만드는 'callback'을 활용해보자.

dataset = windowed_dataset(x_train, window_size, batch_size, shuffle_buffer_size)

model = tf.keras.models.Sequential([
tf.keras.layers.Dense(10, input_shape=[window_size], activation='relu'),
tf.keras.layers.Dense(10, activation='relu'),
tf.keras.layers.Dense(1)
])

lr_schedule = tf.keras.callbacks.LearningRateScheduler(
lambda epoch : 1e-8 * 10**(epoch /20))

optimizer = tf.keras.optimizers.SGD(learning_rate=1e-8, momentum=0.9)
model.compile(loss='mse', optimizer=optimizer)
history = model.fit(dataset, epochs=1000, callbacks=[lr_schedule])

callback을 추가해서 학습률 스케쥴러로 학습률을 조절한 코드이다.
각 epoch 종료 시마다 callback에서 호출하는 것이다.
epoch 숫자를 기준으로 학습률을 값으로 변경한다.
epoch 1에서는 1e-8에 10^(1/20)을 곱한다.
100 epoch에 도달하면 1e-8에 10^5를 곱한다. (100/20)
model.fit에 callback 파라미터를 설정해서 매 callback 마다 이와 같은 현상이 발생한다.

lrs = 1e-8 * (10** (np.arange(100)/20))
plt.semilogx(lrs, history.history['loss'])
plt.axis([1e-8, 1e-3, 0, 300])

이를 통해 학습을 마치고 epoch당 학습률에 대한 epoch당 오차를 플로팅할 수 있다.

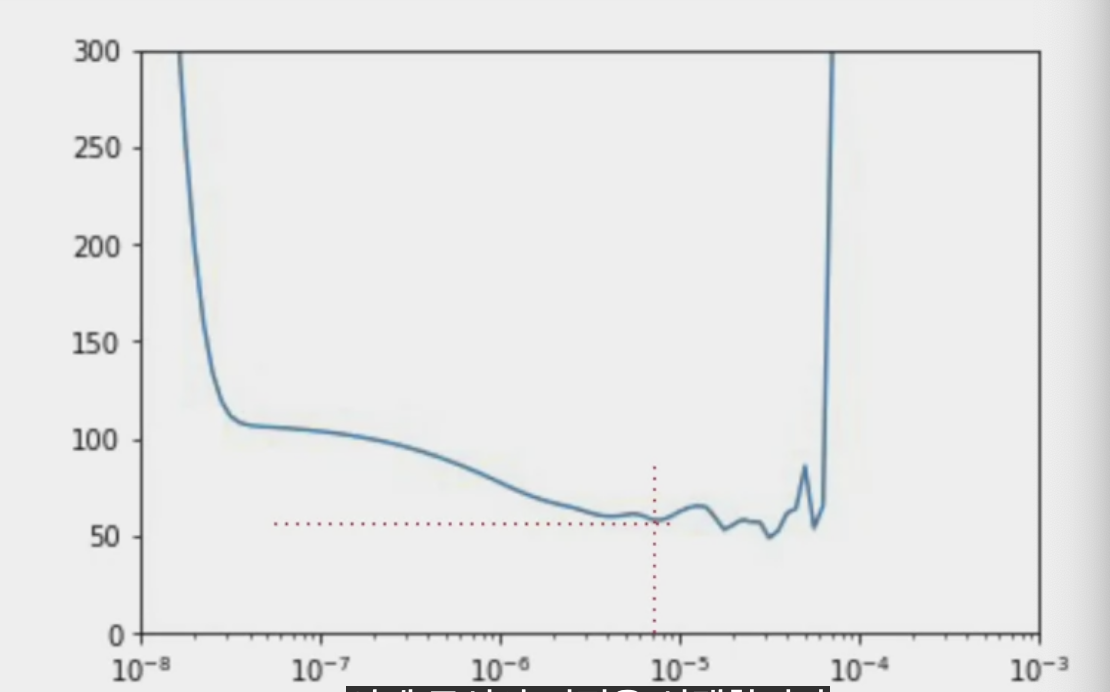
y축은 epoch의 손실, x축은 학습률이다.
곡선의 저점을 선택한다. 10^-6에 7을 곱한 값 정도이다.
이를 학습률로 지정하고 다시 훈련해본다.

window_size =30
dataset = windowed_dataset(x_train, window_size, batch_size, shuffle_buffer_size)

model = tf.keras.models.Sequential([
			tf.keras.layers.Dense(10, activation='relu', input_shape=[window_size]),
            tf.keras.layers.Dense(10, acitvation='relu',
            tf.keras.layers.Dense(1)
            ])
            
optimizer = tf.keras.optimizers.SGD(learning_rate=7e-6, momentum=0.9)
model.compile(loss='mse', optimizer=optimizer)
history = model.fit(dataset, epochs=500)

새로운 학습률로 업데이트하고 더 오랫동안 학습한 것이다.

loss = history.history['loss']
epochs = range(len(loss))
plt.plot(epochs, loss, 'b', label='Training Loss')
plt.show()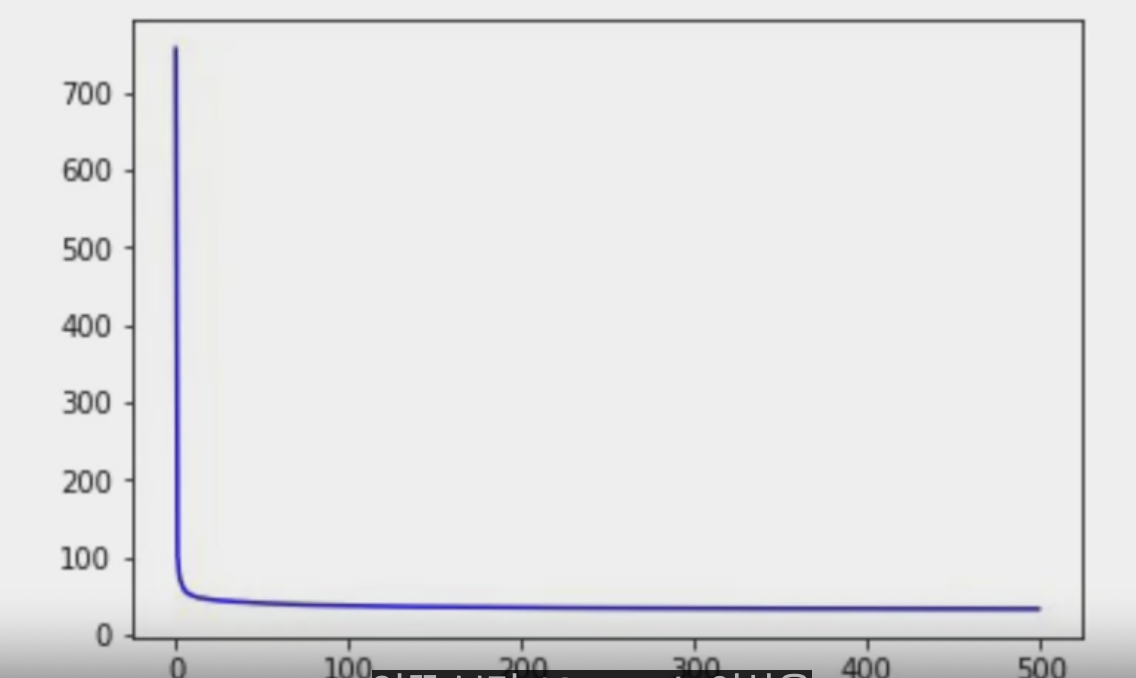

언뜻 보면 10 epoch 이상을 훈련하는 것이 시간 낭비인 것처럼 보이지만
초기 손실이 높아서 사실이 왜곡된 것으로, 이 부분을 잘라내고 10 이후의 epoch 손실을 본다면

loss = history.history['loss']
epochs = range(10, len(loss))
plot_loss = loss[10:]
print(plot_loss)
plt.plot(epochs, plot_loss, 'b', label='Training Loss')
plt.show()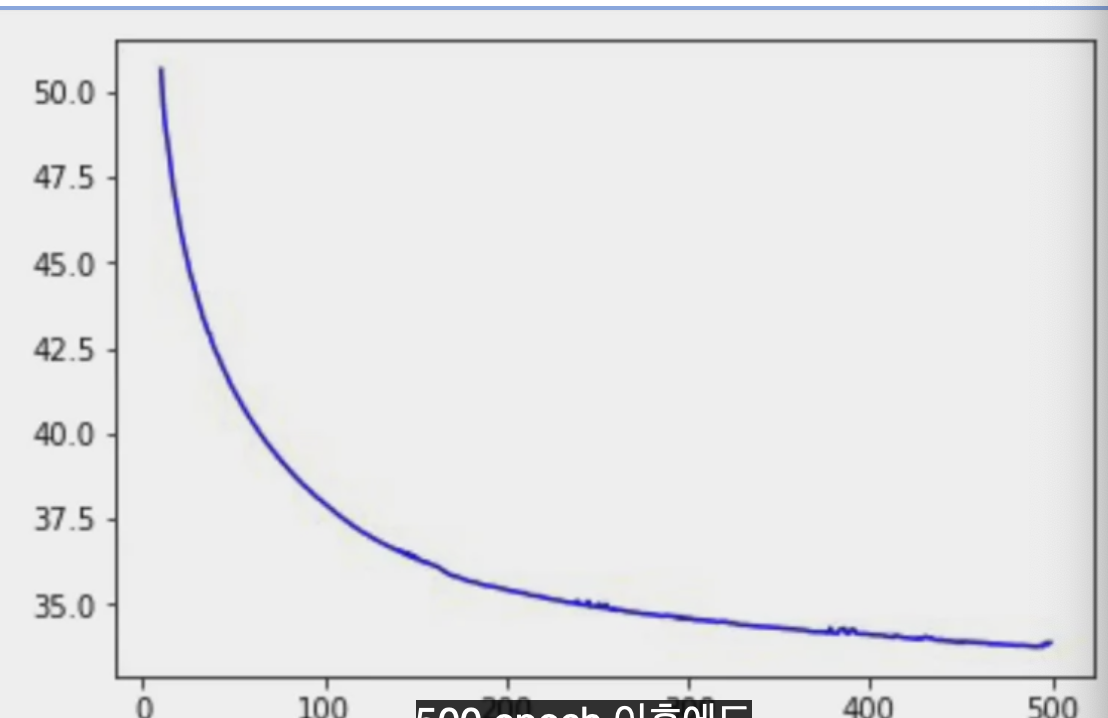

500 epoch 이후에도 loss가 줄어들고 있다.

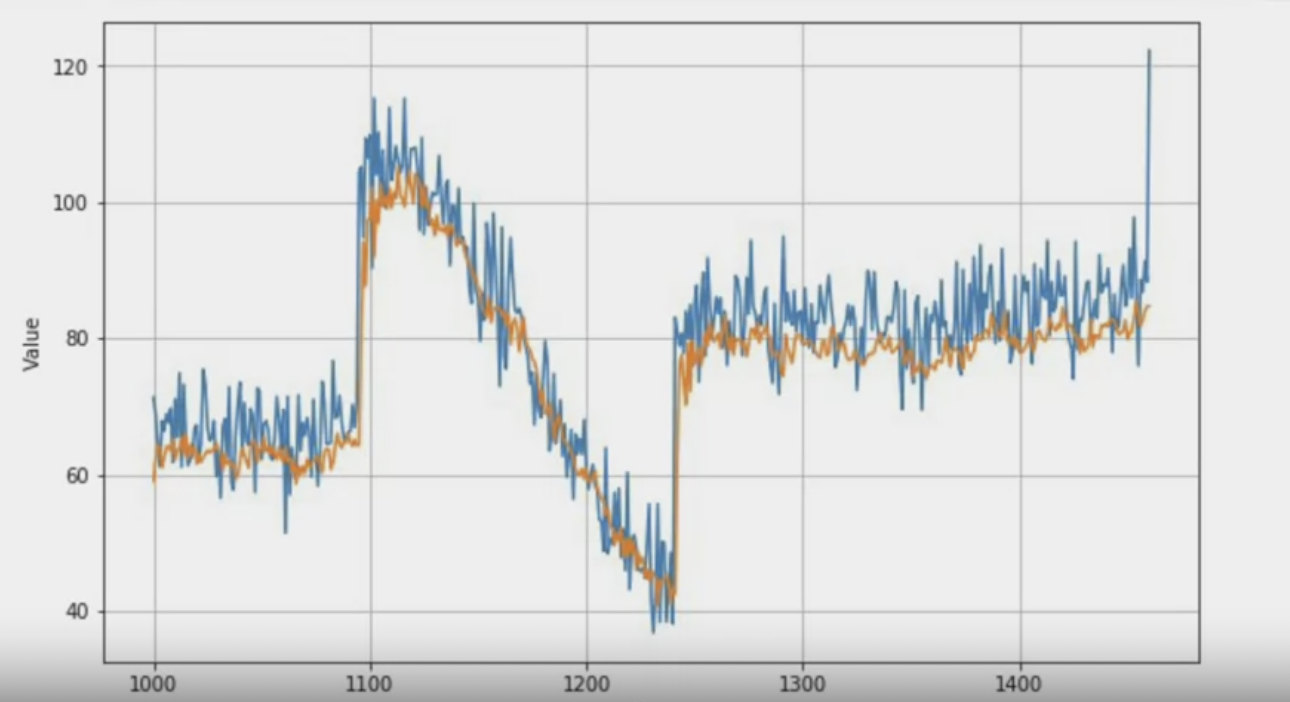
원래의 값에 예측값을 겹치면 위와 같은 차트가 된다.
결과에 대한 평균절대오차는 이전 보다 훨씬 낮아졌다.

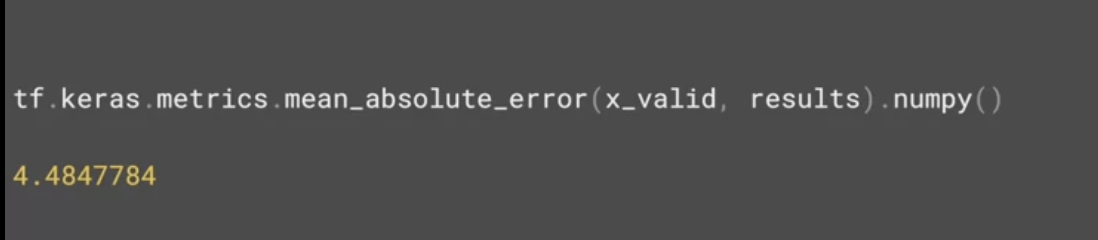
위의 코드는 DNN으로 순차를 고려하지 않았다.
이런 시계열에서는 하나의 값 앞에 있는 값이 과거의 값보다 더 큰 영향을 줄 수 있다.
자연어 처럼 순환 신경망 사용이 좋은 방법일 수 있다.

[9] Deep neural network

워크북을 통해서 이번 강의 전체적인 방법을 코드로 확인한다.
자세한 프로그래밍 방법 및 코드는 새로운 포스팅으로 자세히 작성할 예정이다.

즉, 이번 강의 에서는 시계열 데이터를 통계적 방법 외에
단일 레이어와 딥러닝을 통해서 예측해보는 내용이었다.
또한 딥러닝으로 예측하면서 학습률 파라미터를 조정하는 튜닝도 곁들였다.
다양한 신경망의 정의를 실험하고 레이어를 변경하면서 더 나은 방법들을 찾아본다.