[코딩테스트] Leetcode 1637. Widest Vertical Area Between Two Points Containing No Points

본래 3명의 파이썬 개발자, 1명의 스위프트 개발자, 4명의 코틀린 개발자가 있었으나 다들 취업에 성공하고 이직하면서 우수수 떨어져나감에 따라 혼자서 진행하는 코딩테스트 다시 시작

START :

2023.12.21

Today :

2023.12.21. [1일차]

1637. Widest Vertical Area Between Two Points Containing No Points

https://leetcode.com/problems/widest-vertical-area-between-two-points-containing-no-points/description/

문제 설명

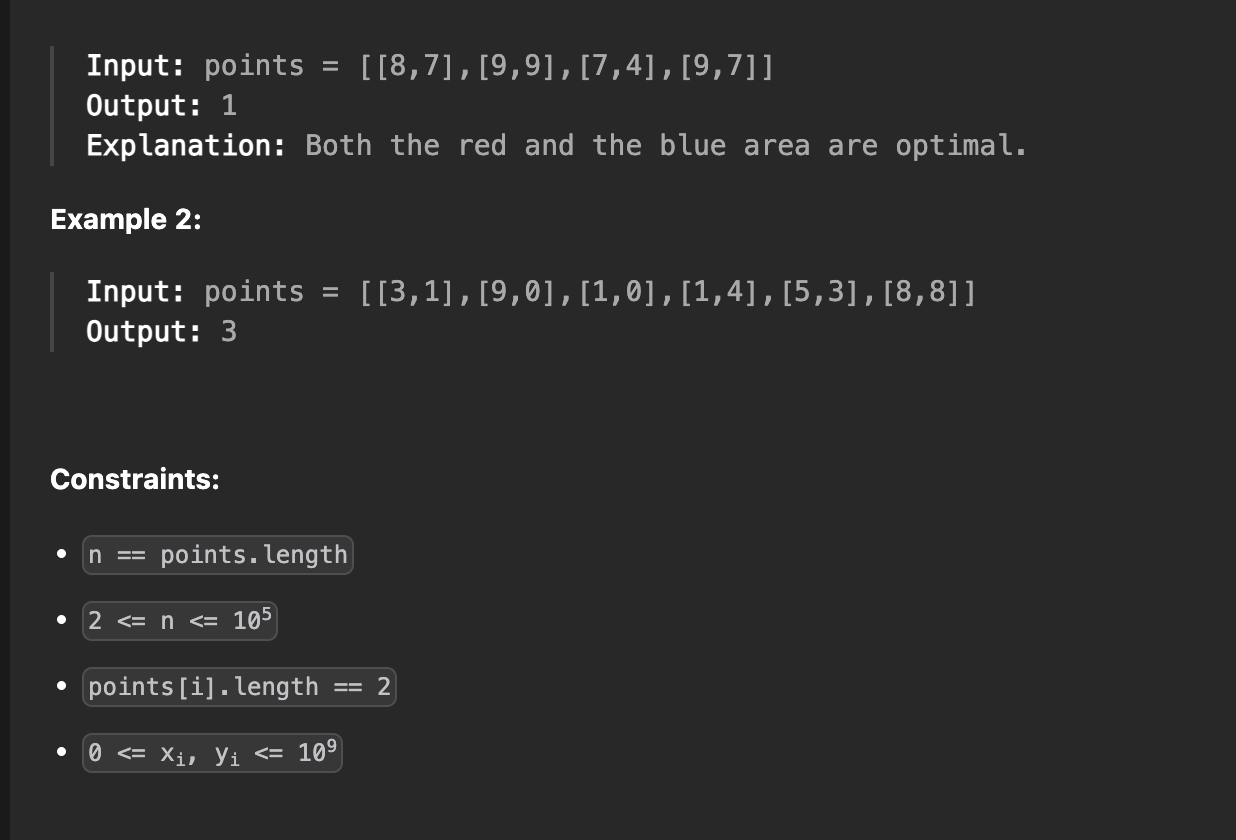
주어진 점들 중에서 x 좌표 값이 가장 차이가 큰 두 점을 선택했을 때, 그 사이의 수직 영역의 너비를 구하는 문제이고, 선택한 두 점은 단일 세로선 상에 있어야 한다.

주어진 점들이 2차원 평면상에 있고 각 점이 (x,y) 형태로 표현될 때,
어떤 두점 (x1,y1), (x2,y2)를 선택했을 때 두 점이 동일한 x 좌표 값을 가지는 경우를 제외하고 선택한 두 점 사이의 너비를 구해야 한다.

너비는 x 좌표의 값으로 측정 되며, 두 점은 단일 세로선 상에 있어야 하는데
예시에 있는 [[8,7],[9,9],[7,4],[9,7]] 에서는
정렬 전: [[8, 7], [9, 9], [7, 4], [9, 7]]
정렬 후: [[7, 4], [8, 7], [9, 7], [9, 9]]

이고 정렬된 점들 간의 x 좌표 차이를 계산하면

첫 번째 점 [7, 4]와 두 번째 점 [8, 7] 간의 x 좌표 차이: 8 - 7 = 1
두 번째 점 [8, 7]와 세 번째 점 [9, 7] 간의 x 좌표 차이: 9 - 8 = 1
세 번째 점 [9, 7]와 네 번째 점 [9, 9] 간의 x 좌표 차이: 9 - 9 = 0
위에서 계산한 x 좌표 차이 중에서 최대값은 1이다.
따라서 이 리스트에서 x 좌표 차이가 가장 큰 두 점은 [8, 7]과 [9, 7]이며, 이 두 점 사이의 수직 영역의 너비는 1이 된다.

example 2와 같은 경우에서도
points = [[3,1],[9,0],[1,0],[1,4],[5,3],[8,8]] 는

정렬 전: [[3, 1], [9, 0], [1, 0], [1, 4], [5, 3], [8, 8]]
정렬 후: [[1, 0], [1, 4], [3, 1], [5, 3], [8, 8], [9, 0]]

이제 이 정렬된 점들 간의 x 좌표 차이를 계산하면

첫 번째 점 [1, 0]와 두 번째 점 [1, 4] 간의 x 좌표 차이: 1 - 1 = 0
두 번째 점 [1, 4]와 세 번째 점 [3, 1] 간의 x 좌표 차이: 3 - 1 = 2
세 번째 점 [3, 1]와 네 번째 점 [5, 3] 간의 x 좌표 차이: 5 - 3 = 2
네 번째 점 [5, 3]와 다섯 번째 점 [8, 8] 간의 x 좌표 차이: 8 - 5 = 3
다섯 번째 점 [8, 8]와 여섯 번째 점 [9, 0] 간의 x 좌표 차이: 9 - 8 = 1
위에서 계산한 x 좌표 차이 중에서 최대값은 3이다.
따라서 이 리스트에서 x 좌표 차이가 가장 큰 두 점은 [5, 3]과 [8, 8]이며,
이 두 점 사이의 수직 영역의 너비는 3이 된다.

내 코드

class Solution:
    def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:
        maxWidth = 0
        x = [point[0] for point in points]
        x.sort()

        for i in range(1, len(x)):
            width = x[i] - x[i-1]
            maxWidth = max(maxWidth, width)

        return maxWidth

증빙