C++ | 재귀함수와 수학

heige·2024년 1월 9일

cpp

CPP

목록 보기

11/12

재귀함수와 수학

재귀함수

재귀함수(Recursion)는 정의 단계에서 자신을 재참조하는 함수
전달되는 상태인 매개변수가 달라질 뿐 똑같은 일을 하는 함수
큰 문제를 작은 부분문제로 나눠서 풀 때 사용합니다.(큰 문제를 쪼개서)

주의사항

반드시 기저사례를 써야 한다.(종료조건)
싸이클을 쓰면 안 된다.
ex) f(a)가 f(b)를 호출한 뒤 f(b)가 다시 f(a)를 호출하는 것
반복문으로 될 것 같으면 반복문으로 해야 한다.(보통은 반복문이 함수호출보다 빠르다.)

예시

팩토리얼(Factorial)

n! = n * (n-1) * (n-2) * ... * 1

f(n) = n * f(n-1)

#include <bits/stdc++.h>
using namespace std;
int fact_rec(int n) {
  if(n == 1 || n == 0) return 1; // 종료조건(기저사례)
  return n * fact_rec(n-1);
}
int fact_for(int n) {
  int ret = 1;
  for(int i = 1; i <= n; i++) {
    ret *= i;
  }
  return ret;
}
int n = 5;
int main(){
  cout << fact_for(n) << '\n';
  cout << fact_rec(n) << '\n';
  return 0; 
}

피보나치

#include <bits/stdc++.h>
using namespace std;

int fibo(int n) {
  cout << "fibo : " << n << '\n';
  if(n == 0 || n == 1) return n;
  return fibo(n-1) + fibo(n-2);
}
int n = 5;
int main(){
  cout << fibo(n) << '\n';
  return 0; 
}

재귀함수를 써야 할 때는 정점과 정점이 상상이 되어야 한다. 호출의 그림이 어느정도 그려져야 한다.
점화식을 보고 구현하면 된다.

순열과 조합

순열 - 순서와 상관 있게 뽑음
조합 - 순서와 상관 없이 뽑음
문제에서 순서를 재배치 해서 max 뽑는 등의 문제 나오면 순열을 생각해야 함

순열

_{n}\mathrm{P}_{r} = {n!\over(n-r)!}

next_permutation과 prev_permutation

C++에서는 next_permutation을 제공한다.
여기엔 시작 지점과 끝 지점이 들어간다. [from, to)
next_permutatio은 오름차순으로 정렬된 배열을 기반으로 순열을 만든다.
prev_permutation은 내림차순을 기반으로 순열을 만든다.

// next_permutation
#include <bits/stdc++.h> 
using namespace std;
int main(){
  int a[] = {1, 2, 3}; 
  do {
    for (int i : a) cout << i << " ";
    cout << '\n';
  }while(next_permutation(&a[0], &a[0]+3));
  return 0;
}
/*
1 2 3 
1 3 2 
2 1 3 
2 3 1 
3 1 2 
3 2 1 
*/

// prev_permutation
#include <bits/stdc++.h> 
using namespace std;
int main(){
  int a[] = {3, 2, 1}; 
  do {
    for (int i : a) cout << i << " ";
    cout << '\n';
  }while(prev_permutation(&a[0], &a[0]+3)); 
  		// (a, a+3)도 가능, vector인 경우 (a.begin(), a.end())
  return 0;
}
/*
3 2 1 
3 1 2 
2 3 1 
2 1 3 
1 3 2 
1 2 3 
*/

#include <bits/stdc++.h> 
using namespace std;

void printV(vector<int> &v){
  for(int i = 0; i < v.size(); i++){
    cout << v[i] << " "; 
  }
  cout << "\n"; }
  
int main(){
  int a[3] = {1, 2, 3}; 
  vector<int> v;
  for(int i = 0; i < 3; i++)
    v.push_back(a[i]); //1, 2, 3부터 오름차순으로 순열을 뽑기
  do{
    printV(v); 
  } while(next_permutation(v.begin(), v.end())); 
  cout << "-----" << '\n';
  v.clear();
  for(int i = 2; i >= 0; i--)
    v.push_back(a[i]); //3, 2, 1부터 내림차순으로 순열을 뽑기 
  do{
    printV(v); 
  } while(prev_permutation(v.begin(), v.end())); 
  return 0;
}
/*
1 2 3 
1 3 2 
2 1 3 
2 3 1 
3 1 2 
3 2 1 
-----
3 2 1 
3 1 2 
2 3 1 
2 1 3 
1 3 2 
1 2 3
*/

주의할 점

next_permutation은 오름차순으로, prev_permutation은 내림차순으로 정렬 후 사용하는 것이 중요하다. 정렬 안 되면 순열의 모든 경우의 수가 나오지 않는다.

// 
#include <bits/stdc++.h> 
using namespace std;
int main(){
  int a[] = {2, 1, 3}; 
  do {
    for (int i : a) cout << i << " ";
    cout << '\n';
  }while(next_permutation(&a[0], &a[0]+3));
  return 0;
}
/*
2 1 3 
2 3 1 
3 1 2 
3 2 1 
*/

그래서 항상 순열을 사용할 때는 sort함수를 이용하도록 한다.

#include <bits/stdc++.h> 
using namespace std;
int main(){
  vector<int> a = {2, 1, 3}; 
  sort(a.begin(), a.end());
  do {
    for (int i : a) cout << i << " ";
    cout << '\n';
  }while(next_permutation(a.begin(), a.end()));
  return 0;
}

순서에 상관있게 두 가지 수를 뽑으라고 하면 ,

#include <bits/stdc++.h> 
using namespace std;
int main(){
  vector<int> a = {2, 1, 3}; 
  sort(a.begin(), a.end());
  do {
    for (int i = 0; i < 2; i++) {
      cout << a[i] << " ";
    }
    cout << '\n';
  }while(next_permutation(a.begin(), a.end()));
  return 0;
}

재귀를 이용한 순열

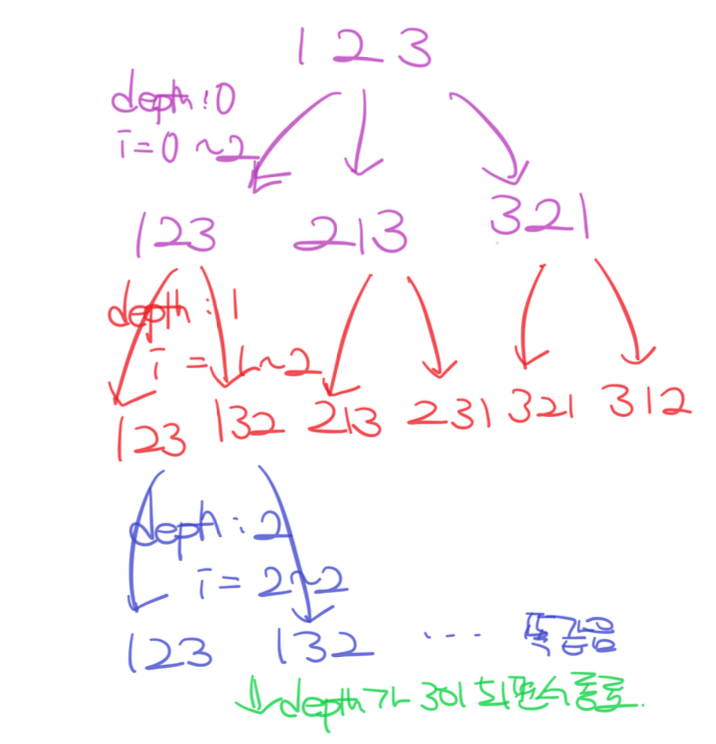
#include <bits/stdc++.h>
using namespace std;
int a[3] = {1, 2, 3};
int n = 3, r = 2; //r을 바꿔가면서 연습해보세요.:) 
void print(){
  for(int i = 0; i < r; i++){ 
    cout << a[i] << " ";
}
  cout << "\n";
}
void makePermutation(int n, int r, int depth){ 
  if(r == depth){
    print();
    return; 
  }
  for(int i = depth; i < n; i++){ 
    swap(a[i], a[depth]); 
    makePermutation(n, r, depth + 1); 
    swap(a[i], a[depth]);
  }
  return; 
}
int main(){ 
  makePermutation(n, r, 0); 
  return 0;
}

재귀를 이용한 순열 - 디버깅코드

#include <bits/stdc++.h>
using namespace std;
int a[3] = {1, 2, 3};
int n = 3, r = 3; //r을 바꿔가면서 연습해보세요.:) 
void print(){
  for(int i = 0; i < r; i++){ 
    cout << a[i] << " ";
}
  cout << "\n";
}
void makePermutation(int n, int r, int depth){ 
  if(r == depth){
    print(); 
    return; // 기저사례 
  }
  for(int i = depth; i < n; i++){ 
    cout << i << " : " << depth << "를 바꾼다!\n";
    swap(a[i], a[depth]); 
    makePermutation(n, r, depth + 1); 
    cout << i << " : " << depth << "를 다시 바꾼다!\n";
    swap(a[i], a[depth]);
  }
  return; 
} 
int main(){ 
  makePermutation(n, r, 0); 
  return 0;
}
/*
0 : 0를 바꾼다!
1 : 1를 바꾼다!
2 : 2를 바꾼다!
1 2 3 
2 : 2를 다시 바꾼다!
1 : 1를 다시 바꾼다!
2 : 1를 바꾼다!
2 : 2를 바꾼다!
1 3 2 
2 : 2를 다시 바꾼다!
2 : 1를 다시 바꾼다!
0 : 0를 다시 바꾼다!
1 : 0를 바꾼다!
1 : 1를 바꾼다!
2 : 2를 바꾼다!
2 1 3 
2 : 2를 다시 바꾼다!
1 : 1를 다시 바꾼다!
2 : 1를 바꾼다!
2 : 2를 바꾼다!
2 3 1 
2 : 2를 다시 바꾼다!
2 : 1를 다시 바꾼다!
1 : 0를 다시 바꾼다!
2 : 0를 바꾼다!
1 : 1를 바꾼다!
2 : 2를 바꾼다!
3 2 1 
2 : 2를 다시 바꾼다!
1 : 1를 다시 바꾼다!
2 : 1를 바꾼다!
2 : 2를 바꾼다!
3 1 2 
2 : 2를 다시 바꾼다!
2 : 1를 다시 바꾼다!
2 : 0를 다시 바꾼다!
*/

⭐️ 재귀함수 도식화 해서 혼자 해보기
⭐️ makePermutation(int n, int r, int depth)함수는 외워두기

조합

순서와 상관없이 다양하게 뽑을 때.

_{n}\mathrm{C}_{r} = {n! \over {r!(n-r)!}}

재귀를 이용한 조합

4개 이상 뽑는 데는 재귀함수, 3개 이하는 중첩 for문 활용하는 게 좋다.

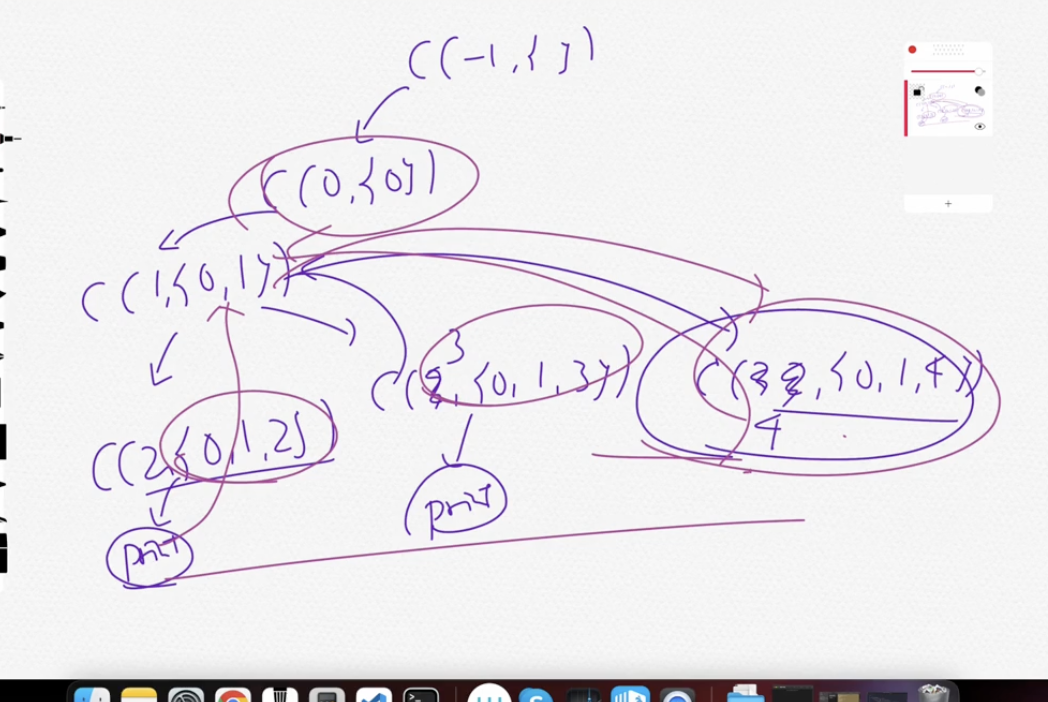
#include <bits/stdc++.h>
using namespace std;
int n = 5, k = 3, a[5] = {1, 2, 3, 4, 5}; 
void print(vector<int> b){
  for(int i : b) cout << i << " ";
  cout << '\n';
}
void combi(int start, vector<int> b){ 
  if(b.size() == k){
    print(b);
    return; 
  }
  for(int i = start + 1; i < n; i++){ 
    b.push_back(i); //i는 index가 들어가는 것
    combi(i, b);
    b.pop_back();
  }
  return; 
}
int main() { 
  vector<int> b;
  combi(-1, b); 
  return 0;
}
/*
0 1 2 
0 1 3 
0 1 4 
0 2 3 
0 2 4 
0 3 4 
1 2 3 
1 2 4 
1 3 4 
2 3 4 
*/

코드가 어떤 흐름을 가질지 이해하는 게 중요하다.
⭐️ 재귀함수 combi(int start, vector<int> b) 외워두기

중첩 for문

#include <bits/stdc++.h>
using namespace std;
int n = 5;
int k = 3;
int a[5] = {1, 2, 3, 4, 5}; 
int main() {
  for(int i = 0; i < n; i++){ 
    for(int j = i + 1; j < n; j++){
      for(int k = j + 1; k < n; k++){
        cout << i << " " << j << " " << k << '\n';
      } 
    }
  }
  return 0; 
}
/*
0 1 2
0 1 3
0 1 4
0 2 3
0 2 4
0 3 4
1 2 3
1 2 4
1 3 4
2 3 4
*/

다음 코드와 순서만 다를 뿐, 같은 의미를 가진다.
순서와 상관없이 뽑는 것이기 때문에!

#include<bits/stdc++.h>
using namespace std;
int n = 5;
int k = 3;
int a[5] = {1, 2, 3, 4, 5}; 
int main() {
  for(int i = 0; i < n; i++){ 
    for(int j = 0; j < i; j++){
      for(int k = 0; k < j; k++){
        cout << i << " " << j << " " << k << '\n';
      } 
    }
  }
  return 0; 
}

만약 r = 2, 2개를 뽑는 거라면?

#include<bits/stdc++.h>
using namespace std;
int n = 5;
int k = 2;
int a[5] = {1, 2, 3, 4, 5}; 
int main() {
  for(int i = 0; i < n; i++){ 
    for(int j = 0; j < i; j++){
        cout << i << " " << j << '\n';
    }
  }
  return 0; 
}
/*
1 0
2 0
2 1
3 0
3 1
3 2
4 0
4 1
4 2
4 3 
*/

조합의 특징 : $_{n}\mathrm{C}_{r} = _{n}\mathrm{C}_{n-r}$

➡️ 순열과 조합은 경우의 수를 기반으로 푸는 문제에 많이 활용된다.

정수론

최대공약수와 최소공배수

최대공약수 `gcd`

int gcd(int a, int b){ 
	if(a == 0) return b; 
    return gcd(b % a, a);
}

최소공배수 `lcm`

최소공배수는 (a * b / (a와 b의 최대공약수)) 로 구한다.

#include<bits/stdc++.h>
using namespace std; 
int gcd(int a, int b){
	if(a == 0) return b;
	return gcd(b % a, a); 
}
int lcm(int a, int b){
	return (a * b) / gcd(a, b);
}
int main(){
	int a = 10, b = 12;
	cout << lcm(a, b) << '\n'; 
    return 0;
}

모듈러 연산

a ≡ b mod과 b ≡ c mod n은 a ≡ c mod n을 의미
[(a mod n)+(b mod n)] mod n = (a+b) mod n
[(a mod n)-(b mod n)] mod n = (a-b) mod n
[(a mod n)*(b mod n)] mod n= (a*b) mod n

에라토스테네스의 체

소수가 아닌 값들에 대한 불리언 배열을 만들어 소수만을 걸러낼 수 있는 방법이다.
다음 코드는 `max_n까지의 소수를 만들어서 출력하는 코드다.

#include<bits/stdc++.h>
using namespace std;
const int max_n = 40;
bool che[max_n + 1];
// 예를 들어 40을 넣었을 때 che[40]이 참조가 되므로 max_n + 1을 넣어야 함. 
// max_n까지의 소수를 만드는 함수
vector<int> era(int mx_n){
	vector<int> v;
	for(int i = 2; i <= mx_n; i++){
		if(che[i]) continue;
		for(int j = 2*i; j <= mx_n; j += i){
			che[j] = 1; 
        }
	}
	for(int i = 2; i <= mx_n; i++) if(che[i] == 0) v.push_back(i); 
    return v;
}
int main(){
	vector<int> a = era(max_n);
    for(int i : a) cout << i << " ";
}

앞의 코드는 배열의 크기가 필요하기 때문에 배열의 크기가 일정 수준(1000만 이상)을 벗어나면 사용하기 힘듦. 이럴 때는 일일이 소수를 판별하는 bool 함수를 만들어주기.

#include<bits/stdc++.h>
using namespace std; 
bool check(int n) {
	if(n <= 1) return 0;
	if(n == 2) return 1;
	if(n % 2 == 0) return 0;
	for (int i = 3; i * i <= n; i++) {
		if (n % i == 0) return 0; 
    }
	return 1; 
}
int main(){
	for(int i = 1; i <= 20; i++){
		if(check(i)){
			cout << i << "는 소수입니다.\n";
		} 
    }
	return 0; 
}

등차수열의 합

\sum_{k=1}^N k = {n(n+1) \over 2}

#include <bits/stdc++.h>
using namespace std; 
int main(){
	ios::sync_with_stdio(0); 
    cin.tie(0); 
    int n = 5;
	int ret = 0;
	for(int i = 1; i <= n; i++){
		ret += i; 
    }
	cout << ret << '\n';
	cout << n * (n + 1) / 2 << '\n'; 
   	return 0;
}

초항, 마지막항, 등차를 알 때,
또 다른 합 공식

S_n = {n(a + l) \over 2}

#include <bits/stdc++.h>
using namespace std; 
int main(){
	ios::sync_with_stdio(0); 
    cin.tie(0); 
    int n = 5;
	int a = 3, l = 23;
	cout << n * (a + l) / 2 << '\n'; 
    return 0;
}

등비수열의 합

a(r^n - 1) \over (r-1)

{a\over(1-r)}

#include<bits/stdc++.h>
using namespace std; 
int main(){
	int a = 1, r = 2, n = 4;
	vector<int> v;
	cout << a * ((int)pow(2, n) - 1) / (r - 1); 
    cout << '\n';
	for(int i = 0; i < n; i++){
       v.push_back(a);
		a *= r; 
    }
	for(int i : v) cout << i << ' ';
    return 0;
}

승수 : `pow()`

#include <bits/stdc++.h>
using namespace std; 
int main(){
	int n = 4;
	int pow_2 = (int)pow(2, n); 
    cout << pow_2 << '\n'; 
    return 0;
}

pow() 함수는 다음 코드 처럼 double형 인자를 2개를 받고 기본적으로 double을 반환한다. 그래서 int형으로 사용하고 싶으면 (int)로 형변환 꼭 해줘야!

pow(double base, double exponent);

제곱근 구하기 : `sqrt()`

#include <bits/stdc++.h>
using namespace std; 
int main(){
	int n = 16;
	int ret = (int)sqrt(n); 
    cout << ret << '\n'; 
    return 0;
}

기본적으로 double형을 매개변수로 받고 double형을 반환한다.

sqrt(double num);

따라서 int형으로 사용하고 싶다면 (int)로 형변환을 꼭 해줘야 한다.

heige

웹 백엔드와 클라우드 정복을 위해 탄탄한 기반을 쌓아가고 있는 예비개발자입니다. 'IT You Up'은 'Eat You Up'이라는 표현에서 비롯되어, IT 지식을 끝까지 먹어치운다는 담고 있습니다.

C++ | 재귀함수와 수학

CPP

재귀함수와 수학

재귀함수

주의사항

예시

팩토리얼(Factorial)

피보나치

순열과 조합

순열

next_permutation과 prev_permutation

주의할 점

재귀를 이용한 순열

재귀를 이용한 순열 - 디버깅코드

조합

재귀를 이용한 조합

중첩 for문

조합의 특징 : $_{n}\mathrm{C}_{r} = _{n}\mathrm{C}_{n-r}$

정수론

최대공약수와 최소공배수

최대공약수 `gcd`

최소공배수 `lcm`

모듈러 연산

에라토스테네스의 체

등차수열의 합

등비수열의 합

승수 : `pow()`

제곱근 구하기 : `sqrt()`

C++ | 배열 수정하기

C++ | using namespace std

0개의 댓글

C++ | 재귀함수와 수학

CPP

재귀함수와 수학

재귀함수

주의사항

예시

팩토리얼(Factorial)

피보나치

순열과 조합

순열

next_permutation과 prev_permutation

주의할 점

재귀를 이용한 순열

재귀를 이용한 순열 - 디버깅코드

조합

재귀를 이용한 조합

중첩 for문

조합의 특징 : nCr=nCn−r_{n}\mathrm{C}_{r} = _{n}\mathrm{C}_{n-r}n​Cr​=n​Cn−r​

정수론

최대공약수와 최소공배수

최대공약수 gcd

최소공배수 lcm

모듈러 연산

에라토스테네스의 체

등차수열의 합

등비수열의 합

승수 : pow()

제곱근 구하기 : sqrt()

C++ | 배열 수정하기

C++ | using namespace std

0개의 댓글

조합의 특징 : $_{n}\mathrm{C}_{r} = _{n}\mathrm{C}_{n-r}$

최대공약수 `gcd`

최소공배수 `lcm`

승수 : `pow()`

제곱근 구하기 : `sqrt()`