[Python] 백준 / gold / 1041번 (주사위)

문제 링크 : https://www.acmicpc.net/problem/1041

재밌는 문제였다.
고려할 케이스가 꽤 많았다.

먼저, N=1인 경우의 주사위는 바닥에 닿은 면을 제외하고 5면이 전부 들어난다.
따라서 5면의 합 중 가장 최소인 것을 출력하면 되는데 이때 함정이 있다.
무작정 min(dice)를 구하면 안되고, 서로 반대편에 있는 면은 더할 수 없다는 점을 고려해야한다.

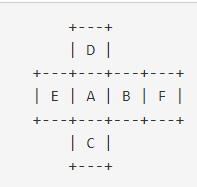
전개도에서 살펴보면 (A,F) (C,D) (B,E) 는 절대 함께 보일수가 없는 면이다.
그래서 N = 1 일때는 이를 고려해서 5면의 합 중 최소값을 구하면 되고,,

N >=2 일때부터는 그림을 그려보면 판단하기가 쉽다.

그림을 그려보면, 주사위중에서 4면이 한꺼번에 보이는 주사위는 절대 나올 수 없다. 최대 3면까지 보일 수 있고, 아예 안보이는 주사위도 존재한다.

3면이 보이는 주사위는 꼭지점 4개 고정,
2면이 보이는 주사위는 4 x (N-1) + 4 x (N-2) 개,
1면이 보이는 주아쉬는 4 x (N-1) x (N-2) + (N-2) x (N-2) 개이다.

opposite 가 포함되지 않은 3면의 합 중 최소를 찾고, 3면이 보이는 주사위 수에 곱해준다. 2면만 보이는 주사위도 마찬가지로 적용한다.

로직을 코드로 구현하면 다음과 같다.

정답 코드

from itertools import combinations
import sys
N = int(sys.stdin.readline())
dice = list(map(int, sys.stdin.readline().split()))
opposite = [(0,5), (5,0), (1,4), (4,1), (2,3), (3,2)]

pair3 = list(combinations(range(6), 3))
pair2 = list(combinations(range(6), 2))

threeSum = 987654321
twoSum = 987654321
oneSum = min(dice)

for a, b, c in pair3:
    if (a, b) in opposite or (b, c) in opposite or (c, a) in opposite:
        continue
    if dice[a]+dice[b]+dice[c] < threeSum:
        threeSum = dice[a]+dice[b]+dice[c]

for a, b in pair2:
    if (a, b) in opposite:
        continue
    if dice[a]+dice[b] < twoSum:
        twoSum = dice[a]+dice[b]

if N == 1:
    possible = []
    for i in range(6):
        possible.append(sum(dice)-dice[i])
    print(min(possible))
else:
    threeFace = 4
    twoFace = 4*(N-1) + 4*(N-2)
    oneFace = 4*(N-1)*(N-2) + (N-2)*(N-2)

    face = [threeFace, twoFace, oneFace]
    face.sort()

    print(threeFace*threeSum + twoFace*twoSum \
          + oneFace*oneSum)