[Python] 백준 / gold / 1655 : 가운데를 말해요

문제 링크 : https://www.acmicpc.net/problem/1655

문제 자체는 단순하지만, 풀이는 꽤 어려웠던 문제. 이 문제의 관건은 입력조건 N 이 10^5 라는 거다. O(N^2) 이상의 알고리즘으로는 시간초과가 나게 돼있다. 최대 O(N*logN) 의 코드를 짜야한다.

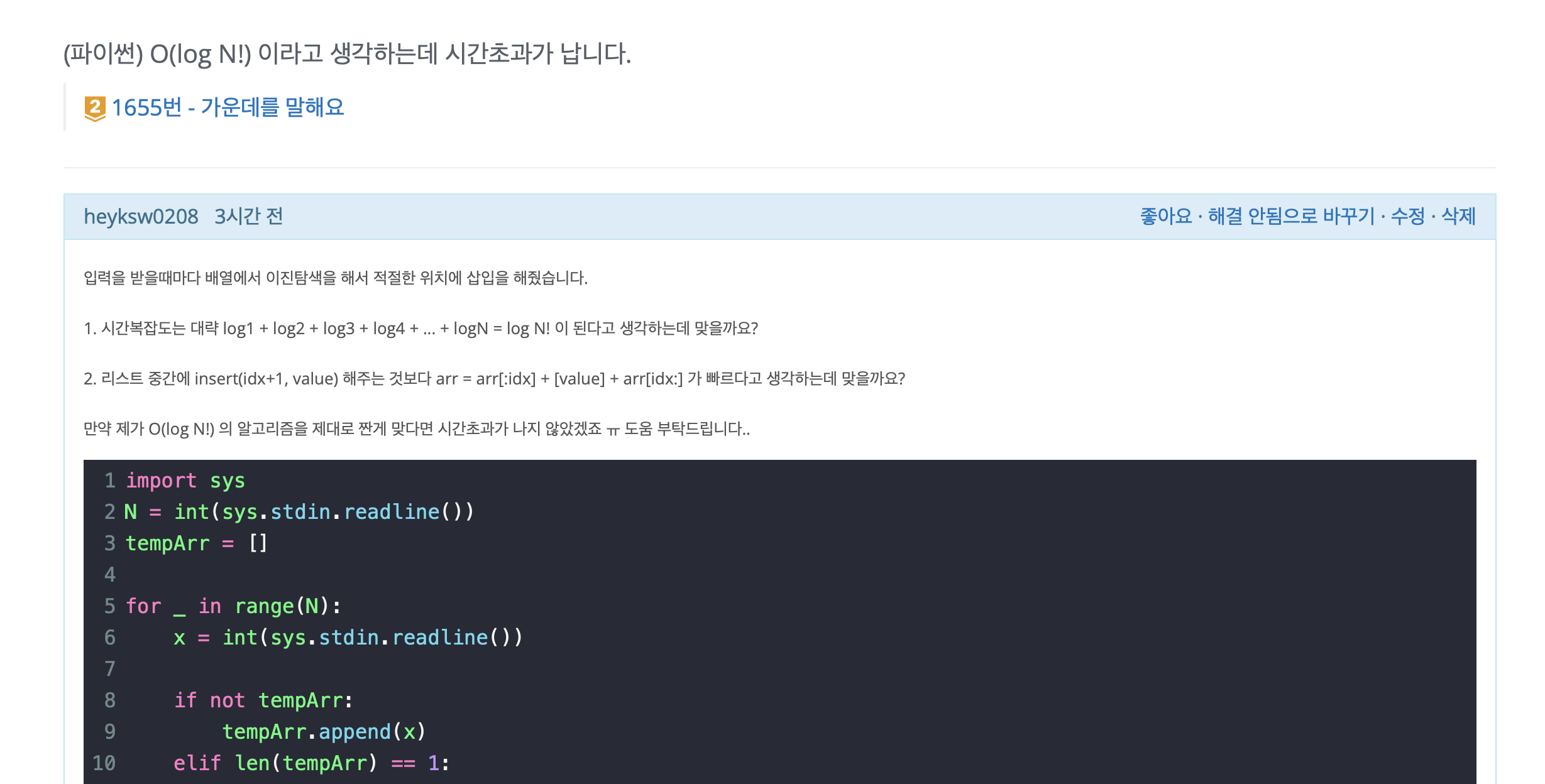
일단 입력조건을 모두 순회해야 되니까 적어도 O(N) 은 확정이다. 그럼 각각 원소들이 O(log N) 의 시간을 사용해야 된다는건데, 그래서 제일 먼저 떠올린건 이분탐색이었다.

원소를 받아들이면서 이분탐색으로 현재 원소가 어느 위치의 인덱스에 들어갈지 결정하는 코드를 짜봤는데 시간초과가 났다.

이분탐색인데 시간초과가 난다고 ..? 사실상 내가 짠 코드의 시간복잡도는 O(log N!) 이라고 생각해서 시간초과가 난다는게 말이 안된다고 생각했다.

오답 코드 - 이분탐색 사용

import sys
N = int(sys.stdin.readline())
arr = []
tempArr = []

for _ in range(N):
    arr.append(int(sys.stdin.readline()))


def getMiddle():
    if len(tempArr) % 2 == 1:
        return tempArr[len(tempArr) // 2]
    else:
        one = tempArr[(len(tempArr) // 2) - 1]
        two = tempArr[len(tempArr) // 2]
        return min(one, two)


def getIndex(value):
    left = 0
    right = len(tempArr) - 1
    answer = 0

    while left <= right:
        mid = (left + right) // 2
        if value < tempArr[mid]:
            right = mid - 1
        elif value > tempArr[mid]:
            left = mid + 1
            answer = mid
        else:
            answer = mid
            break

    return answer


for x in arr:
    if not tempArr:
        tempArr.append(x)
    elif len(tempArr) == 1:
        if tempArr[0] < x:
            tempArr.append(x)
        else:
            tempArr = [x] + tempArr
    else:
        idx = getIndex(x)
        if idx == 0 and x < tempArr[0]:
            tempArr = [x] + tempArr
        else:
            tempArr = tempArr[:(idx + 1)] + [x] + tempArr[(idx + 1):]
    print(getMiddle())

정확한 시간복잡도 계산

진짜 오래 고민하다가 안되겠다 싶어서 게시판에 질문을 올려봤다.

---

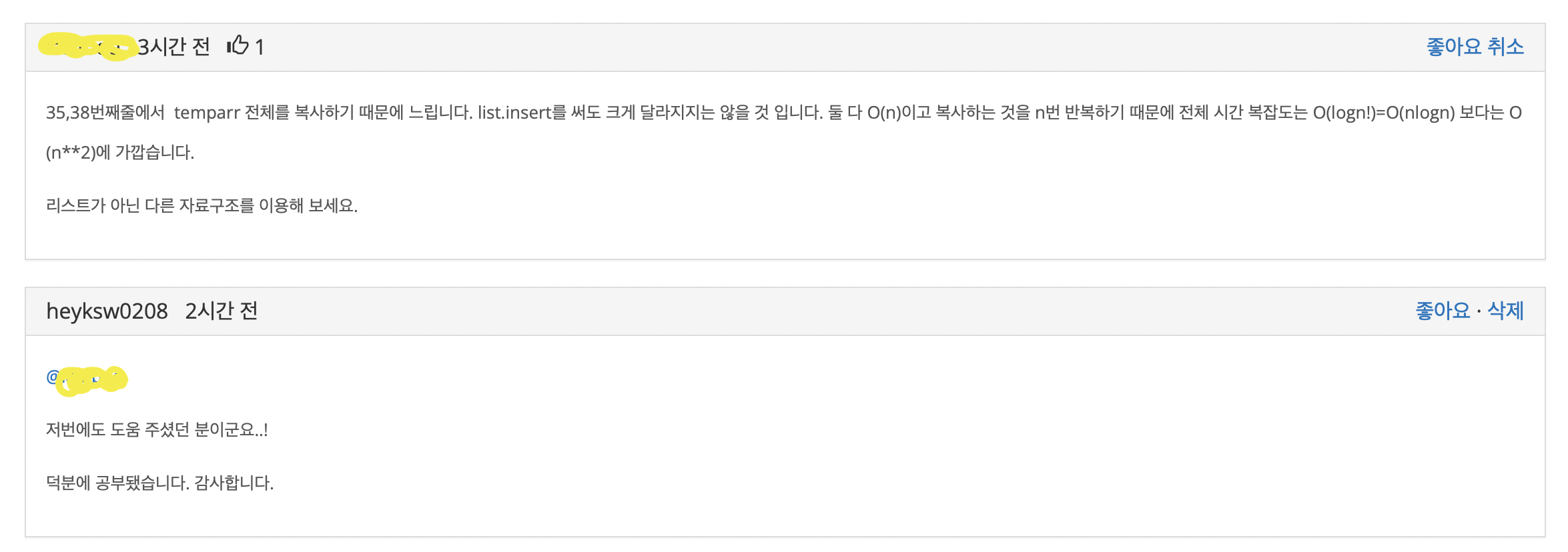
누군가 답변을 주셨다. 감사합니다.. 근데 신기하게도 이분은 내가 예전에 질문 글을 올렸을때도 답변해준 분이였다.

• 결론

이분탐색을 써봤자, 매번 list 를 복사하는 과정에서 시간을 많이 잡아먹기 때문에 사실상은 O(N^2) 에 가까웠다..

그리고 이 문제의 진짜 의도는 이분탐색이 아니라 힙을 사용하는 거였다.

올바른 풀이 - Heap

힙을 2개 사용했다. leftHeap 이라는 MAXheap, rightHeap 이라는 minHeap 을 사용한다. 그리고 where 라는 플래그를 세워서 leftHeap 과 rightHeap 에 번갈아서 원소가 들어가도록 설정했다. 결국 중간값을 찾는 문제기 때문에 Heap 의 최상단에 중간값이 오도록 설정하면 되는 거였다.

leftHeap 에는 상대적으로 작은 원소들이, rightHeap 에는 큰 원소들이 들어가면 된다. 그리고 leftHeap 과 rightHeap 의 원소 개수는 계속 일치시켜준다.

이번 차례가 끝났을 때, leftHeap 의 top 보다 rightHeap 의 top 이 작다면 서로 스왑시켜준다.

이 과정을 반복하면 정답을 낼 수 있었다.

정답 파이썬 코드

import sys
import heapq

N = int(sys.stdin.readline())
arr = []
leftHeap = []
rightHeap = []

for _ in range(N):
    arr.append(int(sys.stdin.readline()))

where = 0
for i in range(len(arr)):
    x = arr[i]
    if where % 2 == 0:
        heapq.heappush(leftHeap, -x)
    else:
        heapq.heappush(rightHeap, x)

    if rightHeap:
        left = heapq.heappop(leftHeap)
        right = heapq.heappop(rightHeap)

        if left * (-1) > right:
            heapq.heappush(leftHeap, right * (-1))
            heapq.heappush(rightHeap, left * (-1))
        else:
            heapq.heappush(leftHeap, left)
            heapq.heappush(rightHeap, right)

        leftTop = heapq.heappop(leftHeap)
        print(leftTop * (-1))
        heapq.heappush(leftHeap, leftTop)

    else:
        leftTop = heapq.heappop(leftHeap)
        print(leftTop*(-1))
        heapq.heappush(leftHeap, leftTop)

    where += 1