[Python] 백준 / platinum / 17831 : 대기업 승범이네

문제 링크 : https://www.acmicpc.net/problem/17831

알고리즘 유형 : 트리 DP 심화

(생각의 흐름)

1. 판매원의 수 (2 <= N <= 200,000) 이므로 완전 탐색하기는 힘들겠다.
   -> 트리 DP로 풀어야겠다고 생각

2. 트리 DP는 i를 루트로 하는 서브트리의 값에 집중한다.
   dp[i][0] = (i를 멘토링에 넣었을 때, i를 루트로 하는 서브트리의 최대 시너지)
   dp[i][1] = (i를 멘토링에 넣지 않았을 때, i를 루트로 하는 서브트리의 최대 시너지)

3. 이 그림을 예시로, 점화식은 다음과 같이 세울 수 있었다.

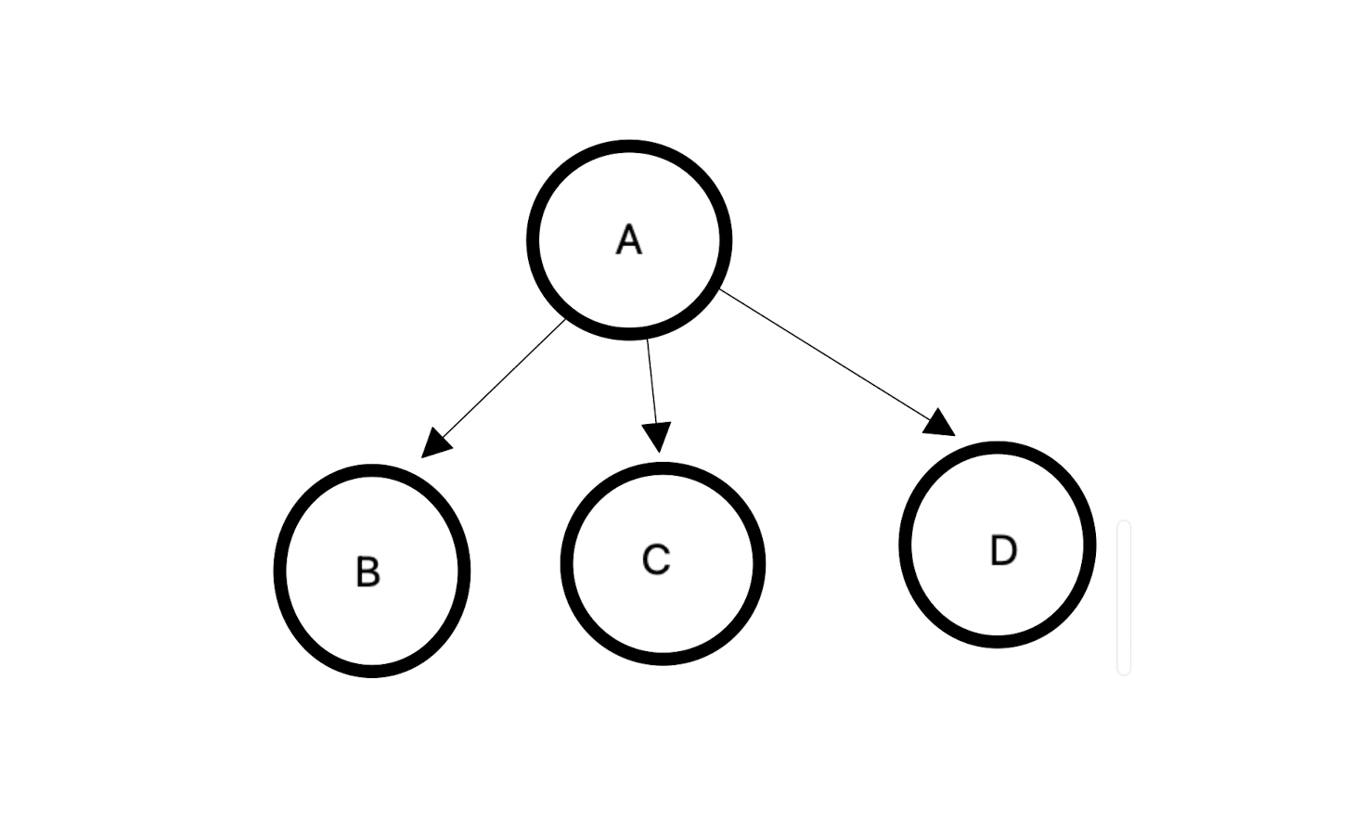
• dp[A][0] = max(dp[B][0], dp[B][1]) + max(dp[C][0], dp[C][1]) + max(dp[D][0], dp[D][1])

• dp[A][1] = max( { W[A]*W[B] + dp[B][0] + max(dp[C][0], dp[C][1]) + max(dp[D][0], dp[D][1]) }, { W[A]*W[C] + dp[C][0] + max(dp[B][0], dp[B][1]) + max(dp[D][0], dp[D][1]), { W[A]*W[D] + dp[D][0] + max(dp[B][0], dp[B][1]) + max(dp[C][0], dp[C][1]) } )

4. dp[node][0] 값은 자식 노드를 DFS 탐색하면서 구할 수 있었고, dp[node][1] 의 값은 자식 노드 중 누구를 멘토링으로 연결할 것인지 선택해야 되기 때문에 2중 for 문으로 로직을 구성했다.

for x in tree[node]:
	for y in tree[node]:
    	if x == y:
        	# 멘토링에 포함
        else:
        	# 멘토링에 포함 x

5. 그런데 N = O(N^5) 이기 때문에 2중 for 문을 사용하면 루트에 모든 노드가 다 붙어있는 특수한 경우는 시간초과가 나게 된다.
   그래서 sum_value = max(dp[child1][0], dp[child][1]) ~ max(dp[childk][0], dp[child][1]) (멘토링에 넣지 않는다고 생각하고 모든 자식들의 max 값을 더한 값)을 미리 구해놓고, 1중 for 문을 순회하면서 멘토링에 넣지 않았던 x 값 (max(dp[x][0], dp[x][1])을 그때 그때 빼주고 멘토링에 넣은 값을 (W[A] * W[x] + dp[x][0]) 더하기로 생각했다. (x 는 현재 순회하고 있는 자식 노드)

6. 그런데 재밌게도 dp 값을 잘 살펴보면 위에서 선언 하려던 sum_value == dp[node][0] 임을 알 수 있었다.
   그래서 dp[node][1] = max(dp[node][1], dp[node][0] - max(dp[x][0], dp[x][1]) + (W[node] * W[x]) + dp[x][0]) (x 는 현재 순회하고 있는 자식 노드) 가 된다.

논리도 억지스럽지 않고, 복잡했던 점화식이 퍼즐처럼 깔끔하게 맞춰져서 간만에 너무 재밌고 좋은 문제를 푼 거 같다.

파이썬 코드

import sys
sys.setrecursionlimit(10**6)
N = int(sys.stdin.readline())
parent = [0] + [0] + list(map(int, sys.stdin.readline().split()))
W = [0] + list(map(int, sys.stdin.readline().split()))
tree = [[] for _ in range(N+1)]
dp = [[0, 0] for _ in range(N+1)]
visit = [False] * (N+1)

for i in range(2, N+1):
    tree[parent[i]].append(i)


def dfs(node):
    visit[node] = True

    for x in tree[node]:
        dfs(x)
        dp[node][0] += max(dp[x][0], dp[x][1])

    dp[node][1] = dp[node][0]
    for x in tree[node]:
        dp[node][1] = max(dp[node][1], dp[node][0] - max(dp[x][0], dp[x][1]) + (W[node] * W[x]) + dp[x][0])


dfs(1)
print(max(dp[1]))