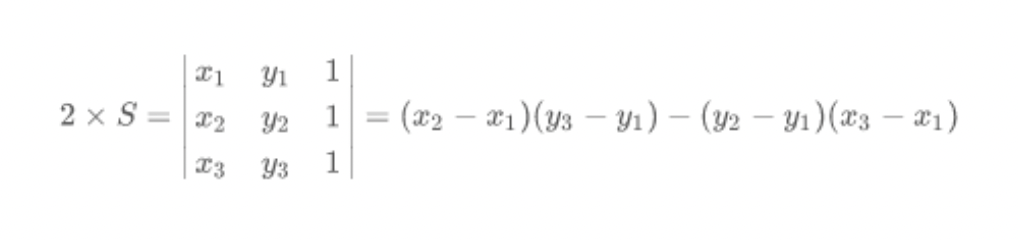[기하학] 두 선분의 관계 파악

reference : 최동완 교수님 강의, https://jason9319.tistory.com/358

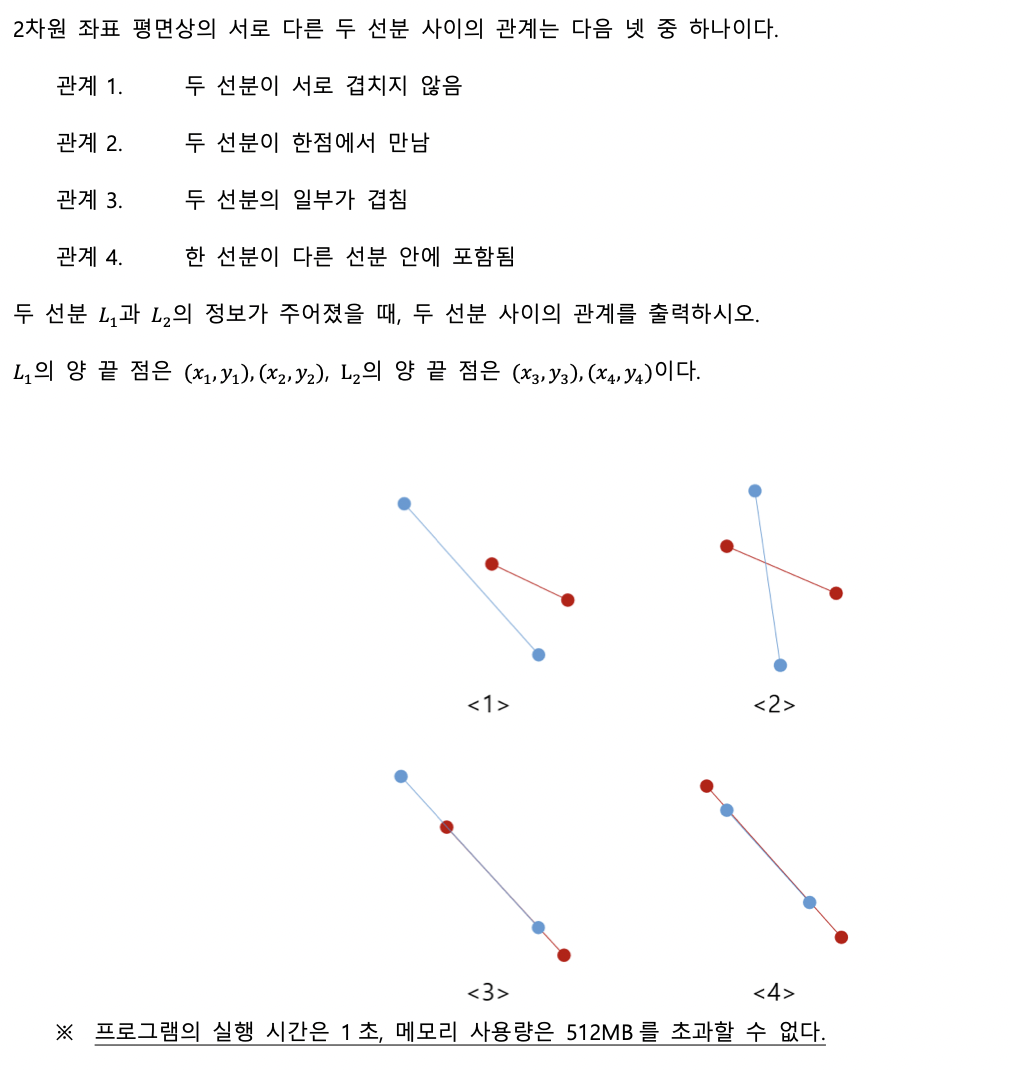
두 선분의 관계 문제

CCW 개념

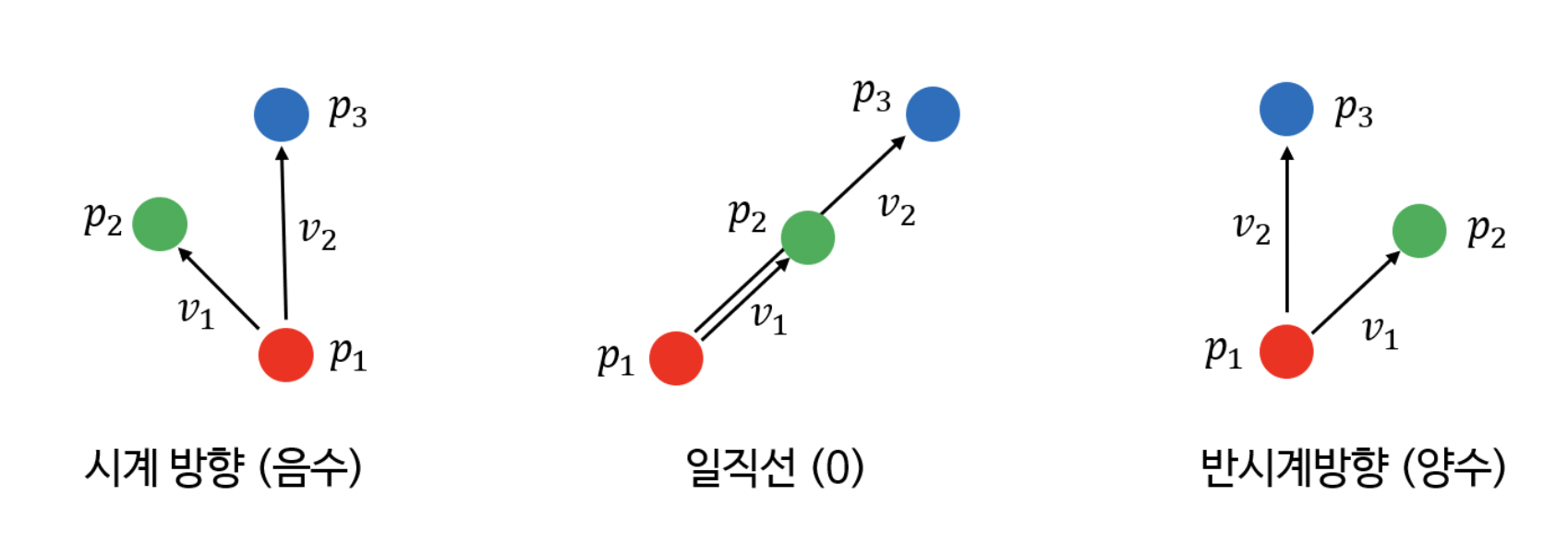
• CCW : Counter ClockWise (반시계 방향)

삼각형을 구하는 공식 + 벡터를 이용하여 CCW 를 구할 수 있다.

CCW 이 값이 양수인 경우는 시계 반대 방향, 음수인 경우는 시계 방향을 뜻한다.

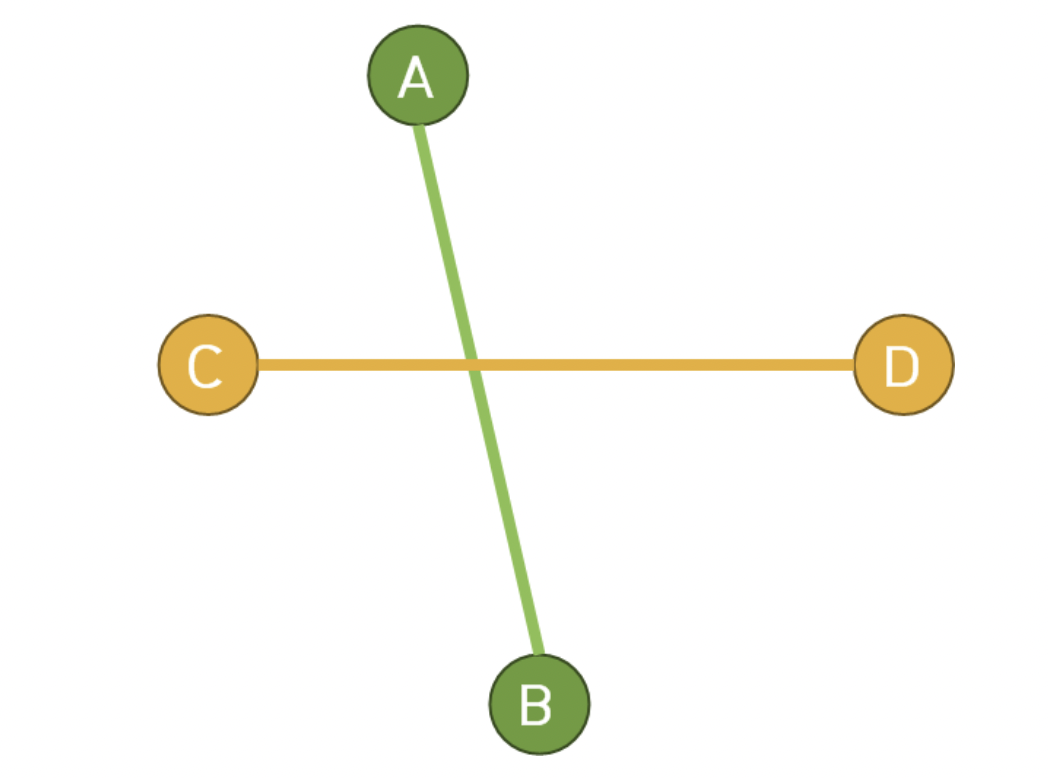
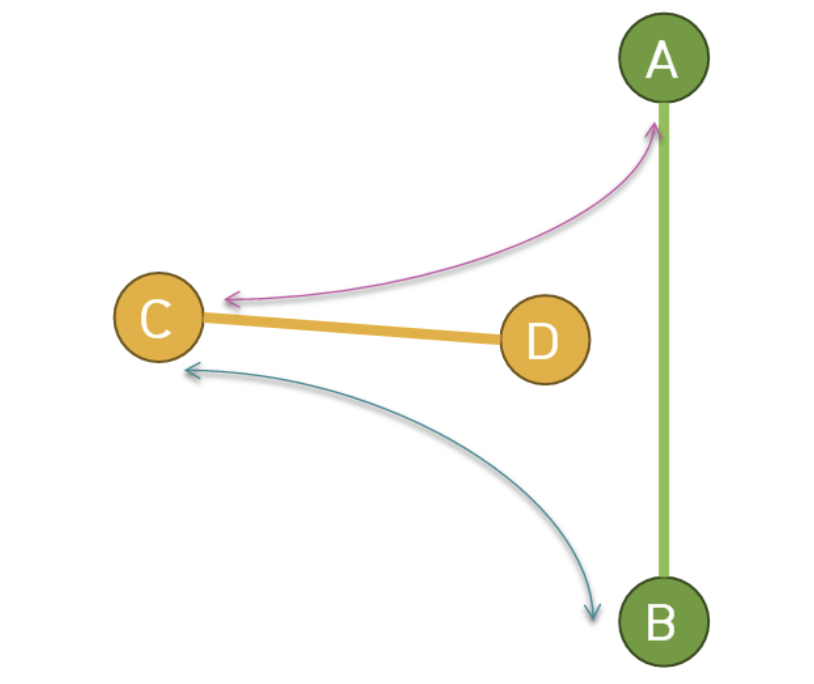
위 그림에서 C->D->A 는 시계 반대 방향,
C->D->B 는 시계 방향으로, 서로 방향이 다르므로 교점이 존재한다고 볼 수 있다.

하지만 위 그림과 같이 예외가 존재하게 되는데,
CCW1 ( C->D->A ) = 양수, CCW2 ( C->D->B ) = 음수를 만족하지만
교점이 존재하지 않는다.
이런 경우는 선분 AB를 기준으로 CCW 를 다시 수행해보면 해결된다.
CCW3 ( A->B->C ) = 음수, CCW4 ( A->B->D ) = 음수 이므로 교점이 존재하지 않는다는 것을 알 수 있다.
그러므로 (CCW1, CCW2) + (CCW3, CC4) 두 번 따져야 완벽한 해를 구할 수 있게 된다.

그리고 한 가지 더 생각해야 할 것이 있는데,

다음의 두 가지 모두 CCW1 == 0, CCW2 == 0 인 경우이다.
두 가지 경우를 로직에서 분리시켜야 한다는 것 까지 고려하면, 두 선분 사이의 관계를 구하는 프로그램을 짤 수 있게 된다.

C++ 정답 코드

#include <iostream>
using namespace std;

// 21x31y 21y31x 로 외웠음.
int ccw(pair<int,int> A, pair<int,int> B, pair<int,int> C){
    int result = (B.first-A.first)*(C.second-A.second) - (B.second-A.second)*(C.first-A.first);
    if(result>0) return 1;
    else if(result==0) return 0;
    else return -1;
}

int relation(pair<int,int> A, pair<int,int> B, pair<int,int> C, pair<int,int> D){
    
    int line1_2 = ccw(A,B,C)*ccw(A,B,D);
    int line2_1 = ccw(C,D,A)*ccw(C,D,B);
    
    // 4개의 점이 모두 한 직선위에 존재하는 경우
    if( line1_2 == 0 && line2_1 == 0){
        if(A > B) swap(A, B);
        if(C > D) swap(C, D);
        
        // 만나지 않는 경우 : 관계 1
        if ( (B<C) || (D<A) ) return 1;
        // 한 점에서 만나는 경우 : 관계 2
        if( (A < C && B == C) || (C<A&&D==A) ) return 2;
        // 두 선분의 일부가 겹치는 경우 : 관계 3
        if( (A<C&&C<B&&B<D) || (C<A&&A<D&&D<B) ) return 3;
        // 한 선분이 다른 선분에 포함 됨
        // 여기 등호 꼭 넣어줘야 함 !! 이것 때문에 엄청 헤맸음 !!
        if( (A<=C&&D<=B) || (C<=A&&B<=D) ) return 4;
                                                
    }
    
    // 모두 그렇지는 않은 경우
    if( line1_2 <= 0 && line2_1 <= 0 ) return 2;
    else return 1;
}

void program(){
    ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
    int x1, y1, x2, y2, x3, y3, x4, y4;
    cin >> x1 >> y1 >> x2 >> y2;
    cin >> x3 >> y3 >> x4 >> y4;
        
    pair<int, int> A(x1, y1);   pair<int, int> B(x2, y2);
    pair<int, int> C(x3, y3);   pair<int, int> D(x4, y4);
    
    cout<<relation(A, B, C, D)<<'\n';

}


int main(){
    ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
    int T;
    cin >> T;
    
    while(T>0){
        program();
        T--;
    }
    return 0;
}

한 선분이 다른 선분을 포함하는 경우는 다음과 같이 두 가지가 있다.
처음에 시작점이 겹치는 밑의 경우를 고려하지 못해서 엄청 헤멨었다.

고민하다가 찾아냈을 때 그 희열 하

C++의 pair<int,int> 로 점을 표현해야 코드가 간결해진다.
pair의 대소 비교는 first를 먼저 비교하고, 그 뒤에 second를 비교하기 때문이다.