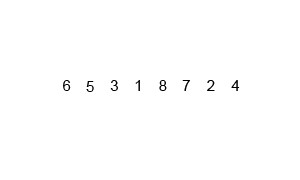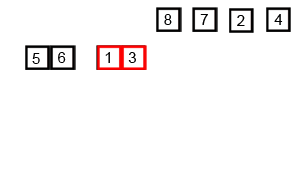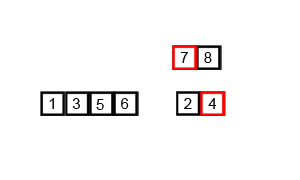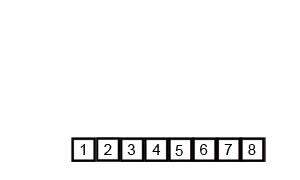출처 : 김병형 교수님 강의, [이것이 코딩테스트다] 도서, 위키 백과
7 가지 정렬 알고리즘 종류
- Bubble sort (버블 정렬)
- Selection sort (선택 정렬)
- Insertion sort (삽입 정렬)
- Quick sort (퀵 정렬)
- Merge sort (합병 정렬)
- Heap sort (힙 정렬)
- Counting sort (계수 정렬)
안전 정렬과 불안전 정렬
- 중복된 값에 대해서 정렬 후에도 그 순서를 유지하는 지에 대한 여부
예를 들어 [2, 1, 1, 3] 이라는 배열이 있을 때,
[2, 1a, 1b, 3] 이라고 별명을 붙이고, 정렬이 끝난 뒤에도 1a, 1b 순서를 유지할 수 있는지.
- 안정 정렬
삽입 정렬, 버블 정렬, 병합 정렬
- 불안정 정렬
선택 정렬, 퀵 정렬
Python의 sort() 함수 (참고)
출처 : https://boying-blog.tistory.com/30
- Python의 sort() 는 팀 피터가 만든 "tim sort"로 구현되어 있다.
- 병합정렬과 삽입정렬을 적절히 섞은 알고리즘이고, 전체적인 기반은 퀵 소트 기반이다. O(N logN) time이다.
- 퀵소트 기반이기 때문에 불안전 정렬이다.
- sort()는 파이썬 내장 파일이기 때문에 C언어로 구현되어 있고, 라이브러리 파일에서는 찾을 수 없다.
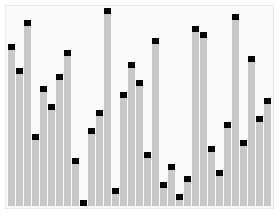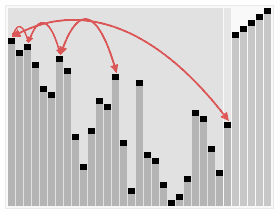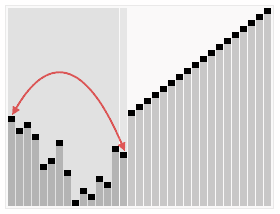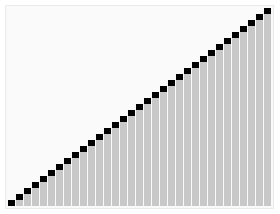
Bubble Sort (버블 정렬)
출처: https://gmlwjd9405.github.io
인접한 두 원소를 검사하며 정렬해나가는 정렬 방법. 원소의 이동이 거품이 수면위로 올라오는 듯한 모습을 보이기 때문에 지어진 이름이다.
단점 : 어떠한 상황에서도 가장 낮은 성능을 보인다.
시간복잡도 O(n^2)장점 : 구현 코드가 간단하기 때문에 자주 사용된다.
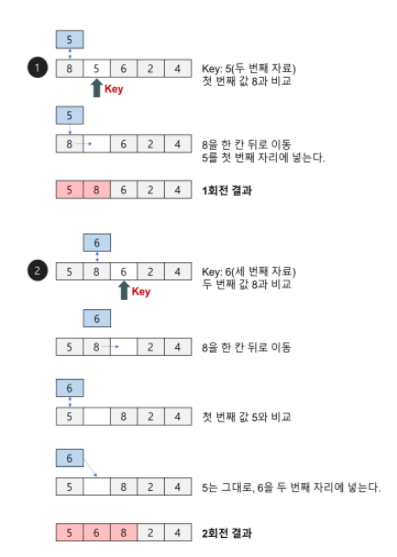
Insertion Sort (삽입 정렬)
출처 : https://gyoogle.dev/blog/algorithm/Insertion%20Sort.html
- 정렬 / 비 정렬 영역을 나누고, 비 정렬 영역의 원소를 정렬된 영역의 적절한 위치에 삽입하는 정렬 알고리즘.
- 집합 내 원소들이 어떻게 비 정렬되어있느냐에 따라 알고리즘의 성능이 달라진다는 특징이 있다.
- 최악의 경우 (반대로 정렬되어 있는 경우) O(N^2) time 소요된다.
- 최선의 경우 (이미 정렬되어 있는 경우) O(N) time 소요된다.
각 단계당 1번씩만 비교 연산이 수행되기 때문이다.- 거의 정렬되어 있는 경우에는 최고의 sorting algorithm 이다.
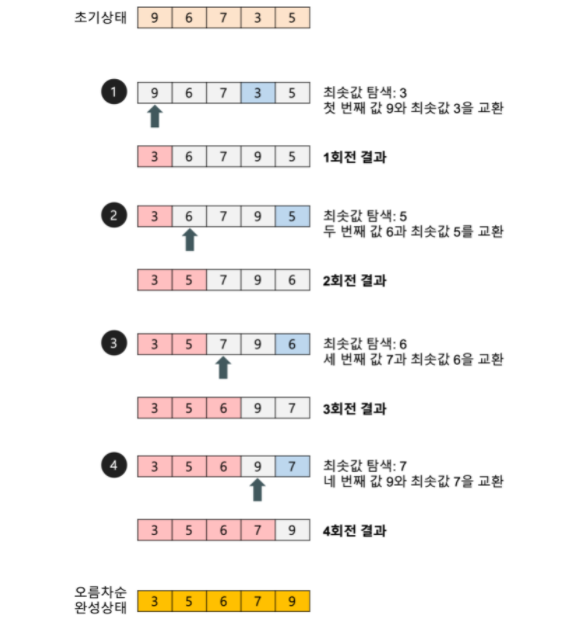
Selection Sort (선택 정렬)
출처 : https://gmlwjd9405.github.io/2018/05/06/algorithm-selection-sort.html
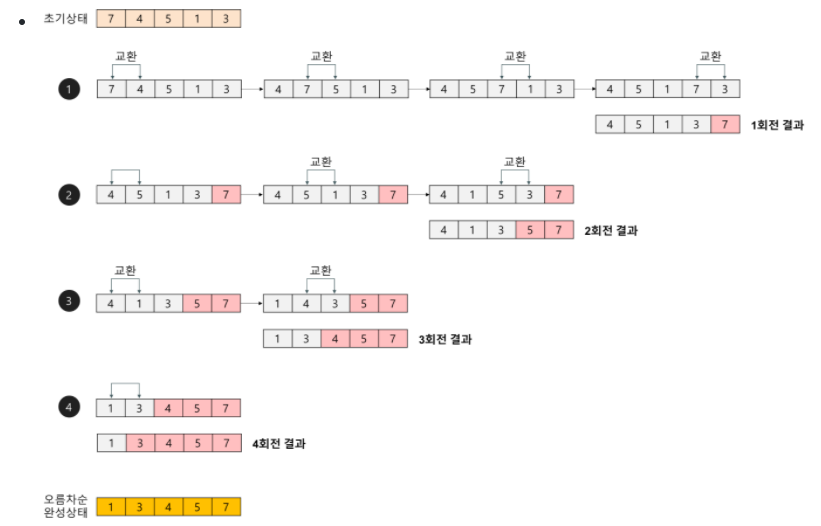
- 매 번 최솟값을 찾아 선택하고, 그 순서에 맞는 위치에 있는 원소와 스왑하는 정렬 알고리즘
- 메모리가 제한적인 경우 사용시 이점이 있다. 추가 메모리 요구 x.
- 제자리 정렬 (in-place) 알고리즘의 하나이다.
- 최선, 최악의 경우 O(N^2) time으로 동일하다.
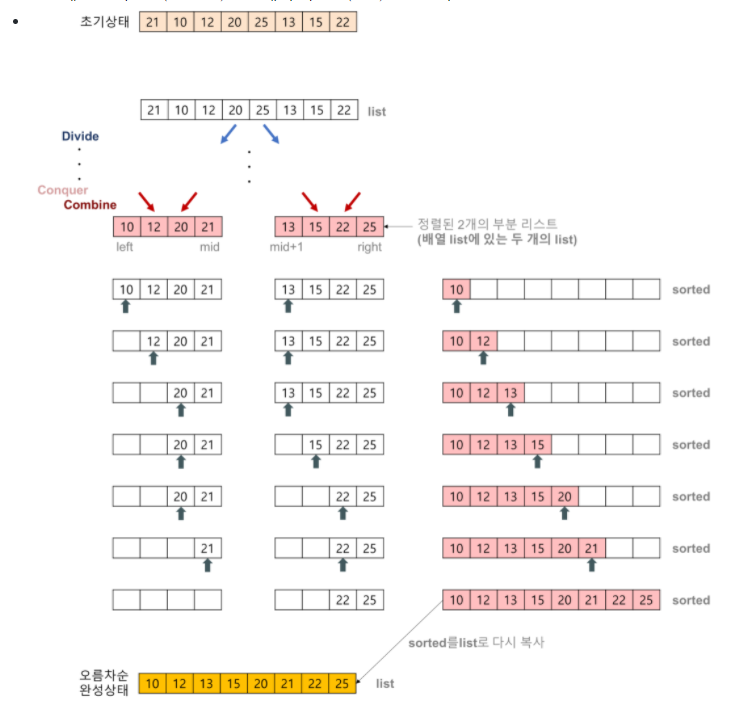
Merge Sort (합병 정렬)
출처 : https://gmlwjd9405.github.io/2018/05/08/algorithm-merge-sort.html
- Divide & Conquer (분할 정복) 알고리즘 중 하나이다.
- 나누고 병합. 합쳐지면서 정렬된다.
- 분할 정복 방법
문제를 2개의 문제로 분리하고 각각을 해결한 다음, 결과를 모아서 원래의 문제를 해결하는 전략. 대부분 순환 호출을 이용하여 구현한다.- 과정 설명
- 리스트의 길이가 0 이나 1이면 정렬된 것으로 본다.
- 비 정렬 리스트를 절반으로 잘라 비슷한 크기의 두 리스트로 나눈다.
- 각 부분 리스트를 재귀적으로 합병 정렬을 이용해 정렬한다.
- 두 부분 리스트를 다시 하나의 정렬된 리스트로 합병한다.
- 단점 : 임시의 데이터 공간이 필요하다 -> in-place 가 아니다.
- 장점 : 데이터 분포에 영향을 받지 않는 편이다. 입력 데이터가 어떤 상태이던 간에 정렬되는 시간은 O(nlogn) time 소요된다.
만약 레코드를 Linked List로 구성한다면, 링크 인덱스만 변경되므로 데이터의 이동은 무시할 수 있을 정도로 작아진다 -> in-place로 구현할 수 있게 된다.
Quick Sort (퀵 정렬)
Pivot (피벗)을 활용하는 정렬 알고리즘. 피벗을 기준으로 작은 요소들은 피벗의 왼쪽으로 옮기고 큰 요소들은 오른쪽으로 옮긴다.
Divide & Conquer에 속한다.
피벗을 어떻게 설정할 것인지가 중요하다.
호어 분할 (Hoare Partition) : 첫 번째 데이터를 피벗으로 설정.
동작 과정 핵심
첫 번째 데이터 x를 피벗으로 설정하고, 왼쪽에서부터 x보다 큰 데이터를 찾아가고 (index left), 오른쪽에서부터 x 보다 작은 데이터를 찾아간다(index right). 찾았을 경우 두 데이터의 위치를 서로 변경한다.
위 과정을 반복하다가, index left와 right가 서로 엇갈리게 되는 순간에는 두 데이터를 서로 바꾸는 것이 아니라, 작은 데이터와 피벗의 위치를 서로 변경한다.
피벗이 이동한 상태에서 피벗 기준 왼쪽 / 오른쪽 Partition을 나누고 각각에 대해 재귀적으로 수행한다.
- 평균적인 시간복잡도는 O(N logN) 이지만, 최악 경우 O(N^2)이다.
- 호어 분할이고, 이미 데이터가 정렬되어 있는 경우 가 최악의 경우이다.
- 오른쪽에서 부터 피벗보다 작은 데이터를 찾아나갈때, O(N) time이 계속 소요되기 때문.
- 그래서 실제로 C++과 같이 퀵 정렬을 기반으로 작성된 정렬 라이브러리를 제공하는 프로그래밍 언어들은 최악 경우에도 O(N logN)이 되는 것을 보장할 수 있도록 피벗값을 설정할 때 추가적인 로직을 더해준다.
- Quick Sort는 in-place / non in-place 두 가지 구현 방법이 있다.
Heap Sort (힙 정렬)
힙 자료구조를 이용하는 정렬 알고리즘
데이터를 힙 구조로 만들고, 힙에서 원소를 하나씩 삭제하며 리스트에 넣으면 그게 정렬된 알고리즘이다.
힙 생성 O(N logN)
힙 삭제 O(log N)
전체 시간복잡도 : O(N logN)
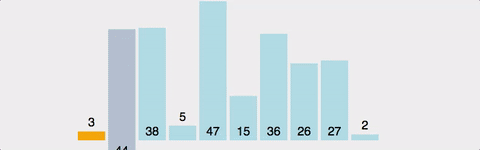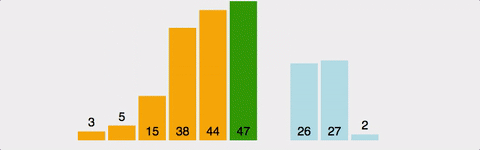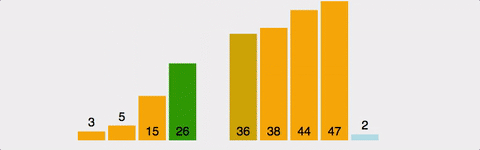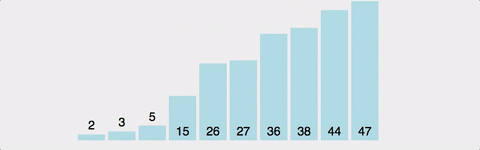
Counting Sort (계수 정렬)
계수 정렬 알고리즘은 특정한 조겁이 부합할 때만 사용할 수 있지만 매우 빠른 정렬 알고리즘이다.
예를 들어, 모든 데이터가 양의 정수인 상황에서 데이터의 개수가 N, 데이터 중 최대값이 K 일때, 계수 정렬은 최악의 경우에도 수행시간 O(N+K)를 보장한다.
"데이터의 크기 범위가 제한 되어 정수 형태로 표현할 수 있을때"만 사용 가능하다.
가장 큰 데이터와 가장 작은 데이터의 차이가 너무 크다면 계수 정렬은 사용할 수 없다. 이런 이유는, 계수 정렬을 이용할 때는 "모든 범위를 담을 수 있는 크기의 별도 리스트(배열)를 선언"해야 하기 때문이다.
정렬 과정
- 데이터를 훑으면서 그 데이터가 몇 번 등장하는지를 의미하는 리스트에 등장 횟수를 저장한다. O(N)
- 횟수를 저장한 리스트를 순회하며 등장 횟수 만큼 출력한다. O(K)
시간복잡도 : O(N+K)
공간복잡도 : O(N+K)
7가지 정렬 알고리즘 비교
장단점 / 안전 불안전 / 시간복잡도