[알고리즘] 투 포인터 / 슬라이딩 윈도우 / Prefix Sum

김상우·2021년 10월 6일

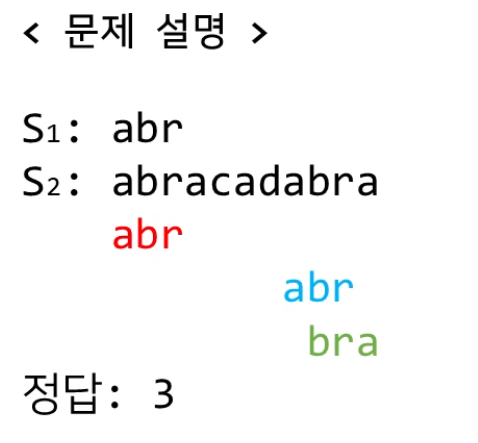
출처 : [이것이 코딩테스트다] 책을 읽고 정리한 내용 +
https://ansohxxn.github.io/algorithm/twopointer/

프로그램을 작성할때나 코딩테스트에서 리스트를 활용하는 경우는 굉장히 많다.
일반적으로 인덱스를 처음부터 끝까지 완전 탐색을 하게 되는데, 완전 탐색을 할 경우 효율성이 좋지 않을 때 활용할 수 있는 알고리즘 3가지는 다음과 같다.

Two Pointer
Sliding Window
Prefix Sum

Two Pointer

리스트에 순차적으로 접근해야 할 때 2개의 점의 위치를 기록하면서 처리하는 알고리즘.

예를 들어, 출석번호 3, 4, 5, 6, 7번 학생이 있을 때 이렇게 번호를 일일히 부르는 것 보다는 "3번부터 7번까지의 학생" 이라고 부르는 것이 효율적이다. 이 3번과 7번이 투 포인터의 두 점이 되는 것이다.

투 포인터 예제 1

문제 ) 양의 정수 리스트에서 특정한 합을 가지는 부분 연속 수열 찾기
listA = [1,2,3,2,5]에서 구간 합이 5인 부분 연속 수열은 몇 가지입니까 ?

정답 코드
A = [1, 2, 3, 2, 5]
K = 5   # 찾으려는 구간 합
start, end = 0, 0
interval_sum = 0
answer = 0

for start in range(len(A)):
    while end < len(A) and interval_sum < K:
        interval_sum += A[end]
        end += 1

    if interval_sum == K:
        answer += 1
    interval_sum -= A[start]

print(answer)
아이디어
start를 for문으로 돌린다. 그 안에서 while문으로 end를 높인다.
만약 interval_sum이 타겟 K 보다 커져버린다면 start를 높여 구간 크기를 줄인다.

투 포인터 예제 2

문제 ) 정렬되어 있는 두 리스트의 합집합 구하기
a = [1,3,5] b= [2,4,6,8] 일 때 정렬된 합집합 리스트를 구하시오.

정답 코드
n, m = 3, 4
a = [1, 3, 5]
b = [2, 4, 6, 8]
c = []
i, j = 0, 0

while i < n and j < m:
    if a[i] <= b[j]:
        c.append(a[i])
        i += 1
        if i == n:
            c += b[j:]
    else:
        c.append(b[j])
        j += 1
        if j == m:
            c += a[i:]

print(c)

Sliding Window

슬라이딩 윈도우 알고리즘

창문 틀에서 창문이 슬라이딩 하는 것 같은 알고리즘이다.

창문의 크기 (W)는 고정이다. 창문이 슬라이딩 한다고 창문 모양이 달라지지는 않는 것처럼,, 그런 의미에서 구간의 크기가 가변적인 투 포인터 알고리즘과 다르다.

슬라이딩 윈도우 예제 1

슬라이딩 윈도우 알고리즘으로 W 크기 구간의 합 구하기

Brute Force 하게 구간 합을 계산하면 O(N x W) time이 소요된다.
하지만 슬라이딩 윈도우 알고리즘을 사용하면 O(N) time이 소요된다.

Brute Force는 합을 계산하는데 O(W) time이 소요되지만, O(1) time이 소요되기 때문이다.

슬라이딩 윈도우 예제 2

Anagram 구하기

Anagram이란 알파벳의 구성은 유지한 채, 순서만 뒤바뀐 단어 관계이다.
ex) listen <-> silent

Prefix Sum

Prefix = 접두사

Prefix Sum = 접두사 합

접두사 합이란 리스트의 맨 앞부터 특정 위치까지의 합을 구해 놓은 것을 의미한다.

알고리즘을 설계할 때 고려해야할 점은, 여러 번 사용될 만한 정보는 미리 구해 저장해 놓을수록 유리하다는 것이다. -> 다이나믹 프로그래밍

그런 의미에서 Prefix Sum은 다이나믹 프로그래밍의 일종이다.

Prefix Sum 예제

구간 합 계산 문제는 여러 개의 Query로 구성되는 문제로 출제되는 경우가 많다. 다수의 구간에 대해서 합을 각각 구하도록 요구된다. 예를 들어 M개의 쿼리가 존재한다고 가정해보자. 각 쿼리는 Left와 Right로 구성되며, 이는 [Left, Right]의 구간을 의미한다. M개의 쿼리가 주어졌을 때, 모든 쿼리에 대하여 구간의 합을 출력하는 문제에 Prefix Sum이 매우 적절하다.

정답 코드
data = [10, 20, 30, 40, 50, 60]
query = [(1, 3), (2, 5), (3, 4)]

prefix_Sum = [data[0]]
for d in data[1:]:
    prefix_Sum.append(prefix_Sum[-1] + d)

for l, r in query:
    if l == 0:
        print(prefix_Sum[r])
    else:
        print(prefix_Sum[r]-prefix_Sum[l-1])
이 경우에 Brute Force 로는 O(N x Q) time 소요,
Prefix Sum 활용 시 O(N + Q) time 소요된다.