[이산수학] 수학적 귀납법 vs 수학적 강귀납법

수학적 귀납법 vs 수학적 강 귀납법

출처 : 김병형 교수님 강의


(자연수 n에 대한 명제 p(n)이 있을 때)

수학적 귀납법의 논리

1. n = 1 일때 p(1)이 참임을 보임
2. n = k 일때 p(k)이 참임을 가정
3. n = k+1 일 때 p(k+1)이 참임을 보임

수학적 강 귀납법의 논리

1. n = 1 일때 p(1)이 참임을 보임
2. n = 1, n = 2, n = 3, ... n = k 가 모두 참임을 가정
3. n = k+1 일 때 p(k+1)이 참임을 보임

강 귀납법 예제

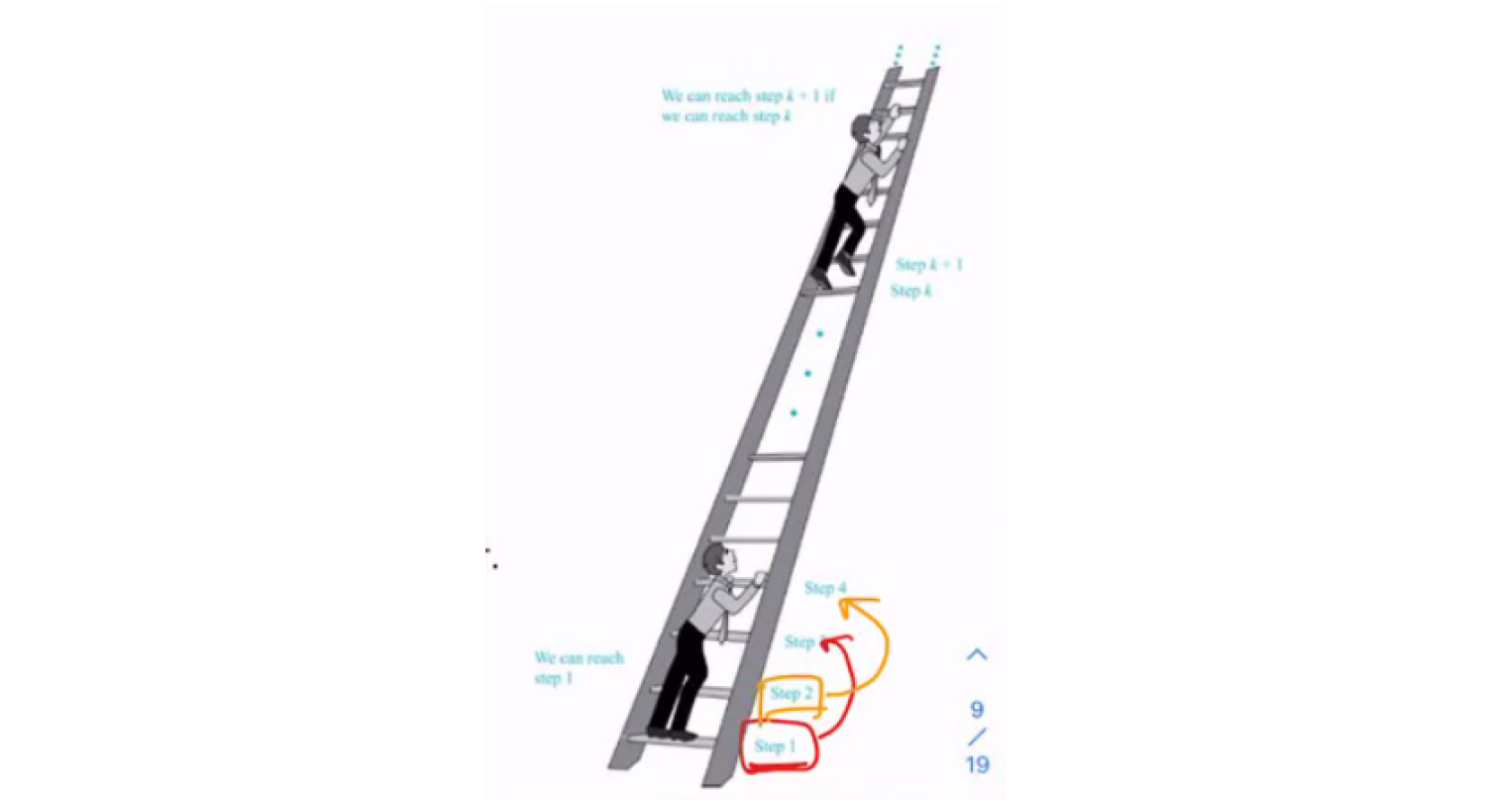
문제) 무한 사다리에서 첫 번째와 두번째 계단에 도달할 수 있다고 하자.
어떤 계단에 도달하면 더 높은 두 개 계단에 도달할 수 있음을 안다고 하자.
모든 계단에 도달할 수 있는가?

강귀납법)
n=1, n=2 성립한다.
n <= k 인 모든 계단에 도달할 수 있다 -> n = k-1 번째 계단에 도달할 수 있다.
그러므로 (k-1) + 2 = k+1번째 계단에 도달 할 수 있다.

귀납법)
n = k번째 계단에 도달할 수 있다 -> n = k+2번째 계단에 도달할 수 있음은 알 수 있지만, k+1 번째 계단은 장담할 수 없다.