요즘은 모델의 학습 과정을 공부하고 있다. 우리에게는 딥러닝 라이브러리가 있으니, backpropagation 계산을 일일이 직접 할 필요은 없겠지만 그 과정을 한번은 정리해
두면 이해하는데 도움이 될 것 같아 전체 과정을 보려고 한다.
backpropagation, 역전파를 간단하게 정의하면 내가 원하는 목표값으로 가기 위해 실제로 모델에서 계산된 출력과의 차이를 계산하여, 그 차이만큼 다시 weight 값을 갱신하는 것의 반복이라고 할 수 있겠다. 출력에서 입력 방향으로 weight 값을 갱신해가기 때문에 "back" propagation 이라고 한다. 말로 하면 쉽다. 하지만 실제 원리를 알기 위해서는 더 자세히
들어가 봐야 한다. 그 전에 먼저 몇 가지 개념을 알고 가자!
chain rule
이름 그대로 chain rule, 연쇄 법칙으로 연쇄로 엮여있는 식을 푸는 것이다. 예를 들어 설명하면 이해하기 쉬운데, 우리는 F(x) = f(g(x)) 에서 f(x) 와 g(x) 가 미분 가능하면, F(x) 도 미분 가능한 것을 알고 있다. 여기서 F(x) 를 x 에 대해 바로 미분하는 것은 불가능하기에, 이 때 chain rule을 사용하여 문제를 해결할 수 있다. 이를 수식으로 표현하면 다음과 같다.
t = g(x), y = F(x) 일 때, F(x) = f(g(x)) 를 미분하면
y' = f'(t) ⋅ (t') -> dy/dx = (dy/dt) ⋅ (dt/dx)
forward propagation
이제 진짜 back propagation의 동작을 뜯어보려면 forward propagation 이 먼저 진행되야
한다. 이름에서도 알 수 있듯이 'forward' 순차대로 진행되는 모델의 학습 과정을 의미한다. neural network, layer에 입력이 들어가면 초기화 된 weight 값과 만나 연산이 이뤄지면서 출력이 나오게 되는 일련의 동작이다. 이 과정을 거치면 우리는 그 결과로 출력을 얻을 수 있는데, 여기서부터 back propagation 이 시작된다.
back propagation
아래 그림은 그림판으로 그린 아주 간단한 모델이다. 입력으로 x0, x1 이 들어가면,
하나의 은닉층 layer Z 와 활성함수 a 를 거쳐 출력으로 y0, y1 가 나오는 구조이다.
여기에서 필요한 가중치는 초기화된 4개의 값이고 활성함수는 sigmoid를 사용한다.
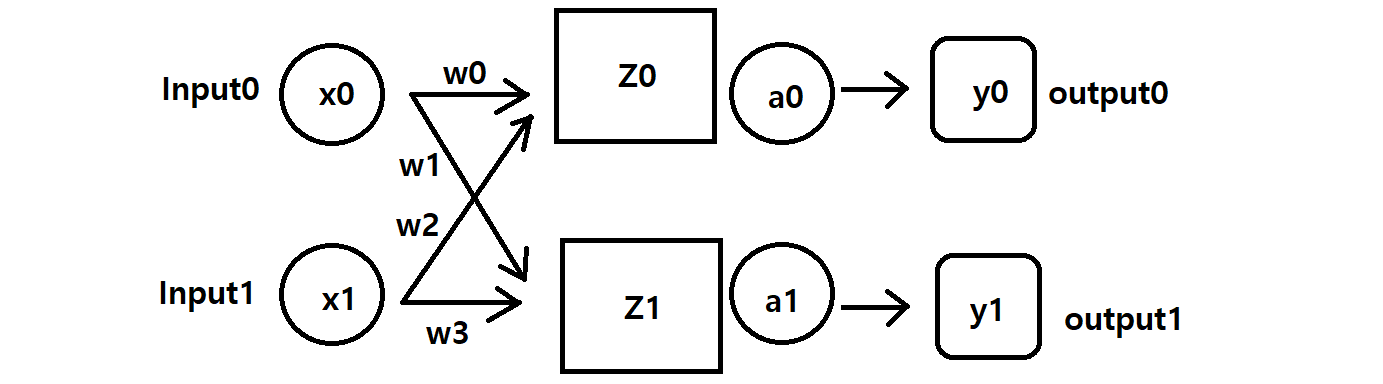
x0 = 0.3, x1 = 0.6 이고 w0 ~ w3은 각각 0.1 ~ 0.4 일 때,
Y0 = 0.2, Y1 = 0.8 의 출력이 나오길 원한다고 가정해 보자
Z0 = (x0⋅w0) + (x1⋅w2) = (0.03) + (0.18) = 0.48
Z1 = (x0⋅w1) + (x1⋅w3) = (0.06) + (0.24) = 0.30
행렬로는 다음과 같이 구할 수 있다.

이 값을 시그모이드에 넣어서 계산기로 계산해보면,
대략 y0 = 0.617 , y1 = 0.574 의 값을 얻을 수 있다.
우리가 원하는 출력값과는 아직 차이가 크다.
오차를 구해보자. 범주형이 아닌 수치형 값이므로 MSE를 사용해보겠다.
( MSE를 모른다면 여기로 --> https://velog.io/@heyme/loss-function )
MSE는 (1/2)⋅∑(오차의 제곱)이므로 ({0.617-0.2}^2 + {0.574-0.8}^2)/2 = 0.1125
이제 chain rule을 이용하여 오차 L에 대한 가중치 w0의 미분을 구해보자
∂E/∂w0 = (∂E/∂a0) ⋅ (∂a0/∂Z0) ⋅ (∂Z0/∂w0) 이렇게 나눠 표현할 수 있다.
왼쪽의 식은 우리가 그 값을 구할 수 없지만, 오른쪽의 식은 구할 수 있다.
① ∂E/∂a0
활성함수를 지나간 값이 출력이므로, L = ({a0 - Y0}^2 + {a1 - Y1}^2)/2 가 되고
이를 a0에 대해 미분하면, ∂E/∂a0 = (a0 - Y0) = (0.617 - 0.2) = 0.417 이 된다.
② ∂a0/∂Z0 : a0 = sigmoid(Z0) 이므로, ∂a0/∂Z0 = 0.236
③ ∂Z0/∂w0 : Z0 = (x0⋅w0) + (x1⋅w2) 이므로, ∂Z0/∂w0 = x0 = 0.3
따라서 ∂E/∂w0 = (0.417) ⋅ (0.236) ⋅ (0.3) = 0.0295, 대략 0.03이 된다.
이제 우리는 오차값 L이 0.1125가 나오도록 하는 w0의 기여도를 알았다. w0의 기여도를 바탕으로 w0의 값을 새롭게 업데이트 해줘야 하는데, 이때 필요한 것이 learning rate이다.
lr은 학습의 속도를 결정하는데 보통 lr = 0.01 정도로 설정한다.
새로 갱신될 w0*의 값 = w0 - (lr*(∂E/∂w0)) = 0.1 - (0.01*0.03) = 0.0097
이렇게 w0의 값은 모델이 원하는 출력을 줄 수 있는 방향으로 수정되었고, 이 과정을 반복할수록 w0의 값은 우리가 원하는 출력을 주는 방향으로 정교하게 갱신될 것이다.
여기서 중요한 것은 변수간의 기여도와 관계성이다. 우리가 원하는 것은 loss가 낮은, 답을 잘 맞추는 모델이다. 그렇다면 loss에 영향을 크게 주는 요인을 찾아서 그 값을 낮출 필요가 있다. 즉, 현재 loss 자체의 값이 의미가 있는 것이 아니라, 그 loss와 관계된 변수가 중요하고 그것이 모델의 성능을 좌우하는 역할을 하게 된다. 이러한 상관관계를 파악하는 수단이 위에서 사용한 미분, chain rule 이고, 알맞는 가중치 값을 찾는 과정이 back propagation가 되는 것이다.
back propagation과 optimizer의 역할을 헷갈렸는데 다시 정리하면,
backpropagation이 가중치를 찾는 하나의 과정이라면, optimizer는 backpropagarion을 어떤 방법으로 모델에 적용시킬지를 찾는 전략이라고 할 수 있겠다. lr을 어떤 비율로 적용시킬지, 어떻게 가중치 비율을 줘야 하는지 결정하는 것은 optimizer의 역할이라고 할 수 있겠다.