1747: 소수&팰린드롬

dohoon·2020년 12월 3일

algorithm brute force number theory 백준 브루트 포스 소수 소수 판정 에라토스테네스의 체 정수론 코딩 테스트 회문

BOJ

목록 보기

1/21

문제 보기

문제 이해

'팰린드롬'은 한국말로 '회문'이라 합니다.
자주 나오는 컨셉이니 익혀두는 것이 좋습니다.

문제가 요구하는 것은 팰린드롬이면서 소수인 수를 찾는 것이네요.
일단, $N$ 은 $10^6$ 이고요.

계획 수립과 검증

그러면 여기서 두 갈래 길이 나옵니다.
1. 팰린드롬 나열 -> 어디에 소수?
2. 소수 나열 -> 어디에 팰린드롬?

팰린드롬은 어떻게 찾을 수 있을까요?

10으로 계속 나눠가서 양쪽 확인을 하면 되죠?
그러면 시간 복잡도는 커봐야 $O(12)$ ! 사실 시간 복잡도라 하기도 뭐하죠.
그냥 상수시간인거에요!

소수는 어떻게 찾을 수 있을까요?

$\sqrt n$ 알고리즘과 에라토스테네스이 체 알고리즘이 있겠죠?
둘의 시간 복잡도는 각각 $O(\sqrt n)$ , $O(n\, log\, n)$ 입니다.
당연히 $\sqrt n$ 알고리즘!
그러면 안됩니다..;;

왜 저게 더 빠른지에 대해 의리적 합심을 해봐야 해요.
전자는 오로지 $n$ 에 대해 소수 판정,
후자는 $n$ 이하의 모든 수에 대해 소수 판정을 합니다.
근데 팰린드롬은 되게 많아요.
4자리수만 봐도
1001, 1111, 1221, 1331, ...
2002, 2112, 2222, 2332, ...
.
.
.
그러면, 에라토스테네스 체가 모든 소수 목록을 만들 수 있으니 좋겠네요.

그러면, 팰린드롬은 상수 시간 취급해버리면 $O(10^6\times 20)$ 정도가 되겠죠?
충분히 가능하다는 겁니다.

그럼 이제 구현..?

그럼 이제 팰린드롬 판정이랑 소수 판정 중에 뭘 먼저 하면 좋을까 생각하죠.
어차피 소수 목록은 전체를 짜기로 했으니, 소수부터 판정하면 되겠네요!

자 이제 코드를 짜볼까요?
네, 아니죠.
위에 훼이크가 있었어요.
만약 이게 풀이였으면 이 문제는 골5가 아니였을 거에요.

N보다 크거나 같고, 소수이면서 팰린드롬인 수 중에서, 가장 작은 수를 구하는 프로그램을 작성하시오.

작은 걸 찾으라는 게 아니랍니다.
뻔한 문제는 아니라 좋군요.

일단 여기에서 '아 에라토스 아니구나, $\sqrt n$ 으로 돌아가야겠어!'라는 생각을 하면 안됩니다.
시간이 안 나온다는 걸 깨달았거든요.
그러면, 에라토스에다가 상한 $x$ 만 쥐어주면 되겠다는 생각을 합니다.

뭔 뜻이냐?
우리는 $n$ 이 증가함에 따라 정답은 항상 단조 증가를 하고 있다는 사실을 알 수 있습니다.
즉, $10^6$ 을 넣어주면 답으로 가능한 것들 중 가장 큰 수가 나올 것이란 거죠.
그러면, 그 가장 큰 수 밑으로만 에라토스를 돌리면 되겠다는 거죠. 그게 상한 $x$ 이고요.

x를 찾자!!

딱 봐도 1000001은 조건을 만족하겠군..!
됐으ㅡㅡ 이러면 안돼요!

엄청 어려운 수학 이론을 통해 검증해야 합니다.

허허;;
이거슨 마리죠 여러분 인수분해를 이용하면 됩니다
$10^6+1 = 100^3+1^3 =$
전 너무 어려워서 못 풀겠네여
그러면 다른 거를 찾아봅시다. 1002001!!
$1001\times 1001$ 임이 너무 자명하군요...
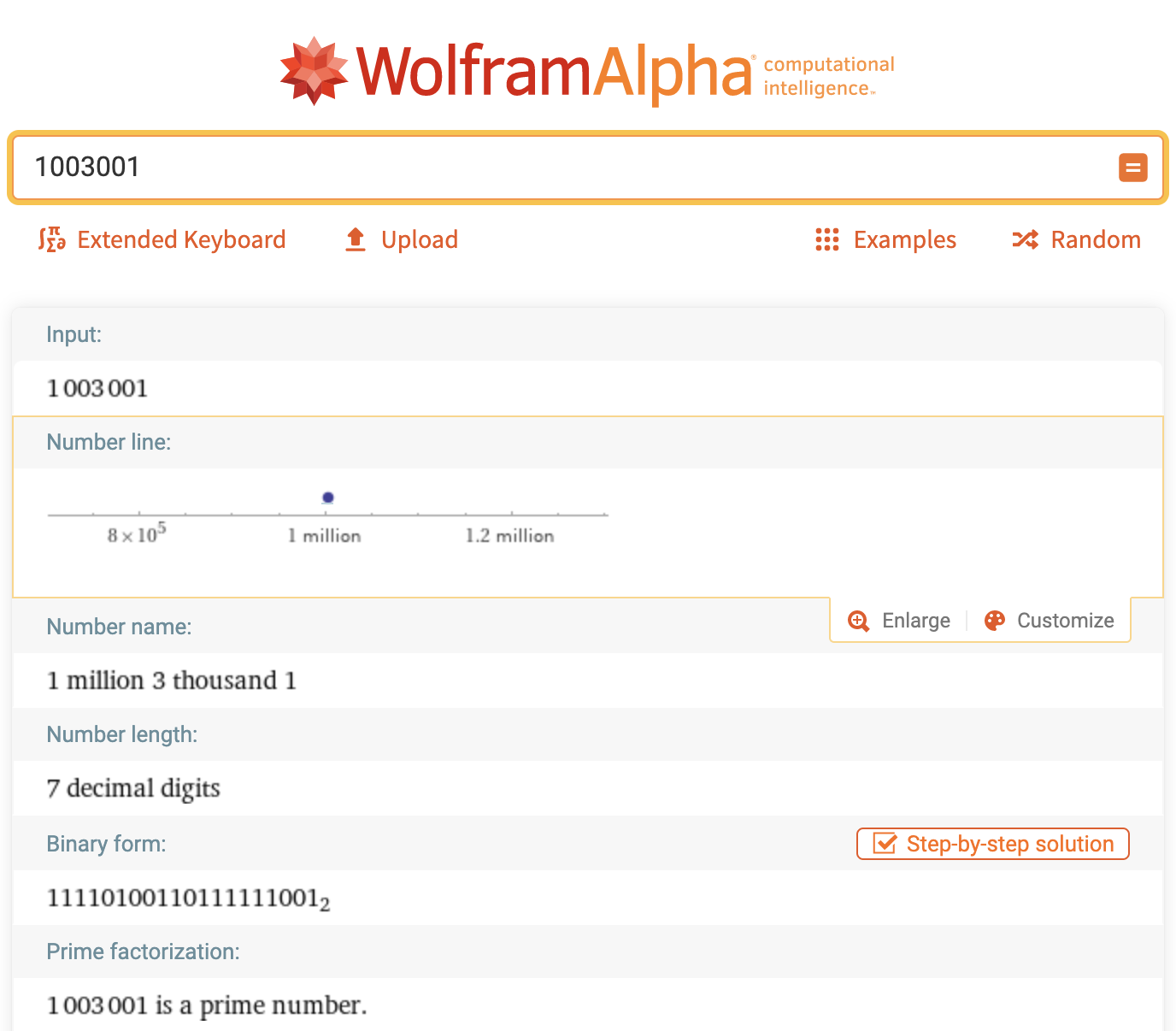
이제 1003001!!
사실 1000까지 다 검사해야 돼서 망했죠.
여건이 된다 -> wolframalpha한테 물어보고,
아니다 직접 하겠다 -> 하시면 코드로 작성해보시면 됩니다. (이때는 $\sqrt n$ 알고리즘이 괜찮죠)
결국 소수라고 합니다.