문제 보기

문제 요약

행렬이 주어진다. 인접한 놈들에 대한 설명을 막 해댄다. 응 그건 알고, 다음!
인접한 두 놈을 잡아서 동시에 $+1$이나 $-1$을 해줄 수 있다.

요게 포인트고요, 목표는 모든 값들을 0으로 만들겠다는 것입니다.

$2\leq R, C \leq 30$이라고 주어집니다...

느낌이...!
딱...!
백트래킹 같죠?

이게 낚시입니다. 범위 그럴 듯하게 적게 줘놓고서는 백트 $NGD$(노가다)시켜가지고 미궁으로 빠지게 만드려는 ICPC의 계략입니다...

문제 풀이

아, 문제 풀이에 앞서 한 가지 간단한 수학적 사실을 짚어봅시다.
$+1$이나 $-1$을 한다는 소리는 $+\alpha$나 $-\alpha$를 하겠다는 소리와 같습니다.
이 정도는 이해하시겠죠?

이건 아주아주 전형적인 불변량 문제입니다. 수학을 많이 해 본 사람이 유리한 유형임에는 틀림없네요ㅠ

설명을 위해 컬러링 기법을 이용합니다.

뭔 소리냐, 싶을 수 있지만 그냥 색칠하겠다는 소리입니다.

다음 상황에서,
어떠한 인접한 두 칸이든 잡아보세요!
하나는 회색, 하나는 흰색임을 관찰하실 수 있나요?

근데, 인접한 두 칸에 대해서 동일한 값을 더하거나 뺀다고 했잖아요?
그러면 회색 칸 수들의 총 합과 흰색 칸 수들의 총 합은 어떻게 될까요?
얘네도 똑같이 움직이겠죠!

그래서 우리의 목표를 달성하기 위해서는 기본적으로,
$($회색 칸 총합$) = ($흰색 칸 총합$)$이 만족되어야 합니다.

이로써 필요조건은 알았습니다.
사실, 충분조건임은 확실하지 않습니다.

그러나, 직관적으로 맞을 것 같죠?
그래서 일단은 구현을 하고 돌아와서 증명하도록 합시다.

구현

아무래도, 빠르게 코드를 작성하는 것이다 보니
다듬는 것 보다는 있는 그대로 보여드리는 것이 좋을 것 같네요...

설마 제가 설명을 위에서 다 해놨는데...
이거 설명까지 할 필요는 없죠?

대신 궁금하신 점은 댓글로 남겨주시면 언제든 답변드립니다.

증명

자, 이제는 회.합과 흰.합이 동일하다면 항상 가능함에 대해서...
즉, 그것이 필요충분조건임에 대해서 생각해보도록 합시다.

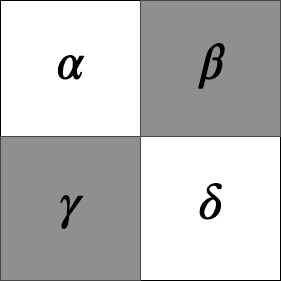
다음과 같은 부분이 있다면...

여기에서 $\alpha$와 $\delta$간의 값 이동이 가능하다면 충분하다는 것은 이해가 되겠지요? (안 되면 댓글로 질문주세요)

편의상, 얘네가 다 0에서 시작한다고 합시다. (변화에 집중하므로 0인 것은 상관이 없습니다.)



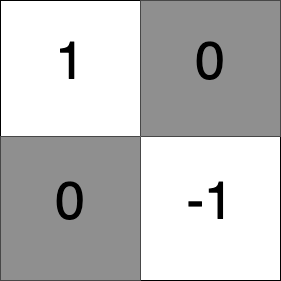
네, 가장 가까운 같은 색 칸과 최소 단위로 값 이동이 일어날 수 있음이 증명되었습니다. ∎