tistory에서 옮겨왔습니다.
후기
폭설이라 버스가 밀렸다...
그래서 핸드폰으로 어떻게든 출제를 했지만,
실수로 E번을 이진탐색+세그를 내버렸다...
이건 명백한 나의 실수이다... 앞으로는 주말에 다 골라놓아야겠다...
그거 빼고는 나는 만족스러웠다.
A번은 최적화 LIS를 공부하고 싶은 마음에 넣었지만, 풀지 못했다.
Ⓐ 가장 긴 증가하는 부분 수열 2 (12015)
by papergundam
LIS(최장 증가 부분 수열)문제입니다.
배열의 최대값보다 i번째 값이 더 크다면 배열에 넣어주고 그렇지 않을경우 i번째 값의 lower_bound를 구해서 그 위치 값을 i번째 값으로 변경해주면 됩니다.
lower_bound란 val값보다 큰 값들 중에 가장 작은 값의 위치를 반환하는 함수입니다.
lower_bound를 해주는 이유는 가장 긴 증가하는 수열을 만들어야 하기때문에 자신의 값보다 더 작은 값이 올수 있으면 더 작은 값이 오게 해서 가장 긴 증가하는 수열을 만들어 주는 것입니다.

Ⓑ 내리막 길 (1520)
by hgmhc
DP 문제입니다.
그래프에 대한 감만 확실히 있다면 풀 수 있을 것 같습니다.
그렇지만 어려웠던 것은 인정합니다. TLE가 날 것 같지만 그래프 순회를 몇 번 이용했고,
결국 3번만에 풀어냈는데... 그 방법은 미리 DP로 찾을 값들이 위치한 곳들을 표시해 놓는 것이었습니다.
(약간 말이 이상한데...)
그러니까, 무작정 DP를 쓰면 완전하지 않은 값들을 참조할 것이고, 무작정 그래프 순회를 이용해도 원하는 곳까지 도달하는 것이 곤란합니다. 따라서 누울 자리를 미리 봐두고 누워야 한다는 거죠...
그래서 자신의 좌표에 도달하기 위한 방향들을 미리 찾아놓는 겁니다.
이를 바탕으로 에서부터 탑다운 방식으로 값들을 참조하여 경우의 수를 완성하는 겁니다.
결국 전처리 과정을 제외하고 나면 으로 상당히 속도가 개선됩니다.
뭔가 설명이 어설펐지만... 댓이나 DM 남겨주시면 안되는 부분들 자세하게 설명드릴게요!

Ⓒ 상근이의 여행 (9372)
by hgmhc
트리라는 이름 아래 부끄러운 그런 문제이다.
완전그래프를 이루는 트리에서는 항상 이다.
(모르시면 참고하세요[난이도 하] - 그래프 기본 용어)
트리라는 이름 아래 부끄러운 그런 문제이다.
완전그래프를 이루는 트리에서는 항상 이다.
(모르시면 참고하세요[난이도 하] - 그래프 기본 용어)

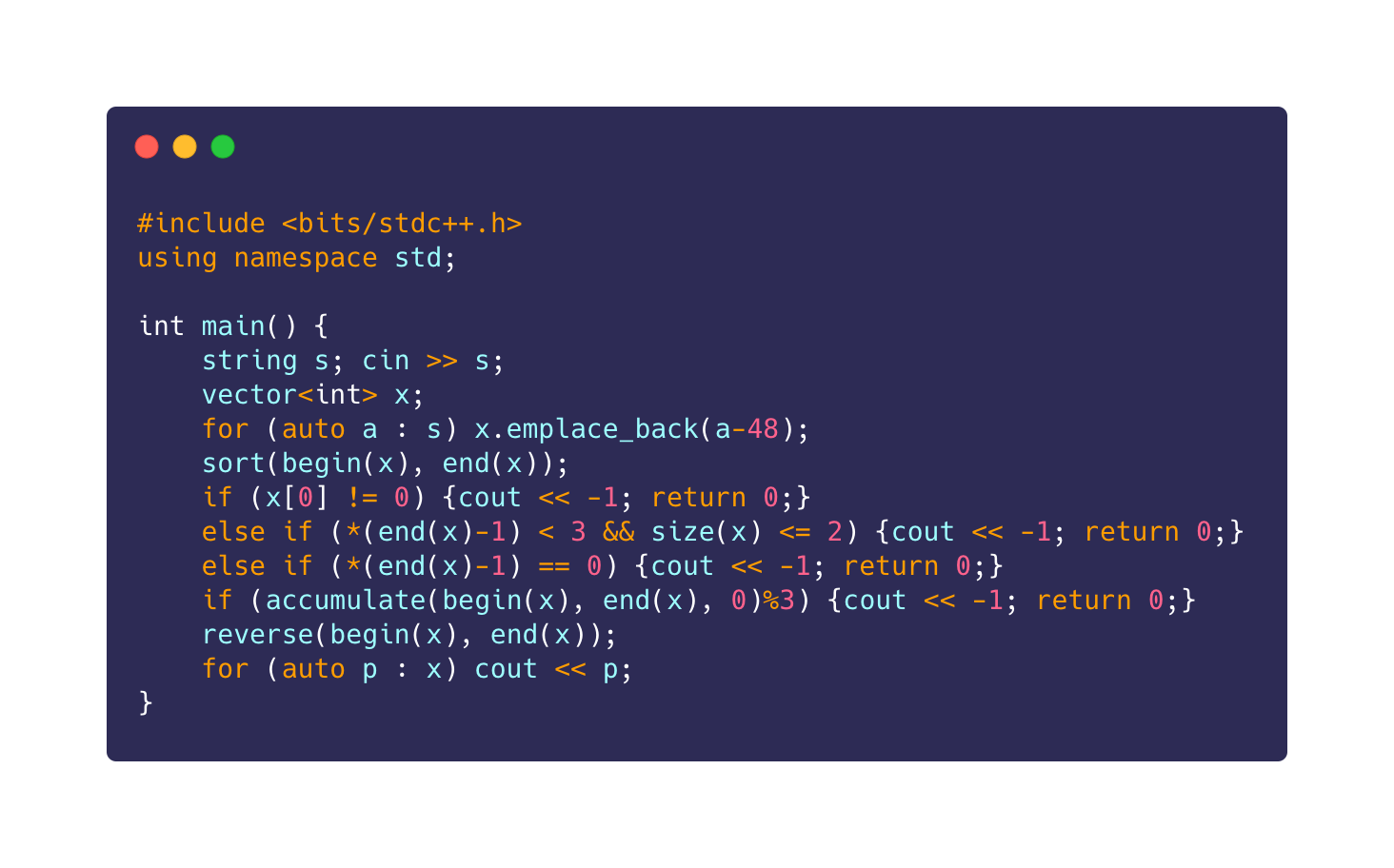
Ⓓ 30 (10610)
by hgmhc
30의 소인수 분해에 대해 생각해보면 쉽게 풀 수 있다.
약간의 Case Work라고 생각하면 된다. 질문은 역시나 댓/DM으로~
30의 소인수 분해에 대해 생각해보면 쉽게 풀 수 있다.
약간의 Case Work라고 생각하면 된다. 질문은 역시나 댓/DM으로~