그래프 자료 구조와 DFS, BFS

그래프란?

• 연결되어 있는 개체 간의 관계를 표현할 수 있는 자료 구조
• 어떤 자료나 개념을 표현하는 정점(Vertex, Node)들의 집합과 이들을 연결하는 간선(Edge)들의 집합으로 이루어짐.

그래프의 특성과 활용

• 현실 세계의 사물이나 추상적인 개념 간의 연결 관계 표현
• 도로망, SNS 지인 관계, 웹 사이트 링크, 네트워크 등에서 활용
• 부모 자식 관계와 같은 제약 사항이 없기 때문에 훨씬 다양한 구조 표현 가능

기타 자료 구조와의 비교

• 관계를 표현 → 연결 리스트
• 순서를 표현 → 큐, 스택
• 계층 구조를 표현 → 트리
• 관계의 방향, 정도(가중치), n:n 등 복잡한 관계 표현은 그래프로 가능

관련 용어

• undirected graph : 엣지가 방향성을 갖지 않는 그래프
• directed graph : 엣지가 방향성을 갖는 그래프
• weighted graph : 가중치를 갖는 그래프
• degree : edge의 개수
  - 들어오는 화살표 : in-degree
  - 나가는 화살표 : out-degree
• cycle : 출발과 도착이 같은 경로들의 집합
• complete graph : 모든 vertex가 다른 vertex와 adjacent 형태로 연결되어 있는 형태.

그래프의 표현

1. 연결 리스트
   -연결된 엣지 리스트를 표현
   -엣지의 개수가 많이질 경우 메모리 소요가 큼
2. 행렬
   -서로 간에 연결되어 있는지 여부를 2차원 배열로 구현
   -불필요하게 메모리를 낭비하게 되는 단점이 있음
   

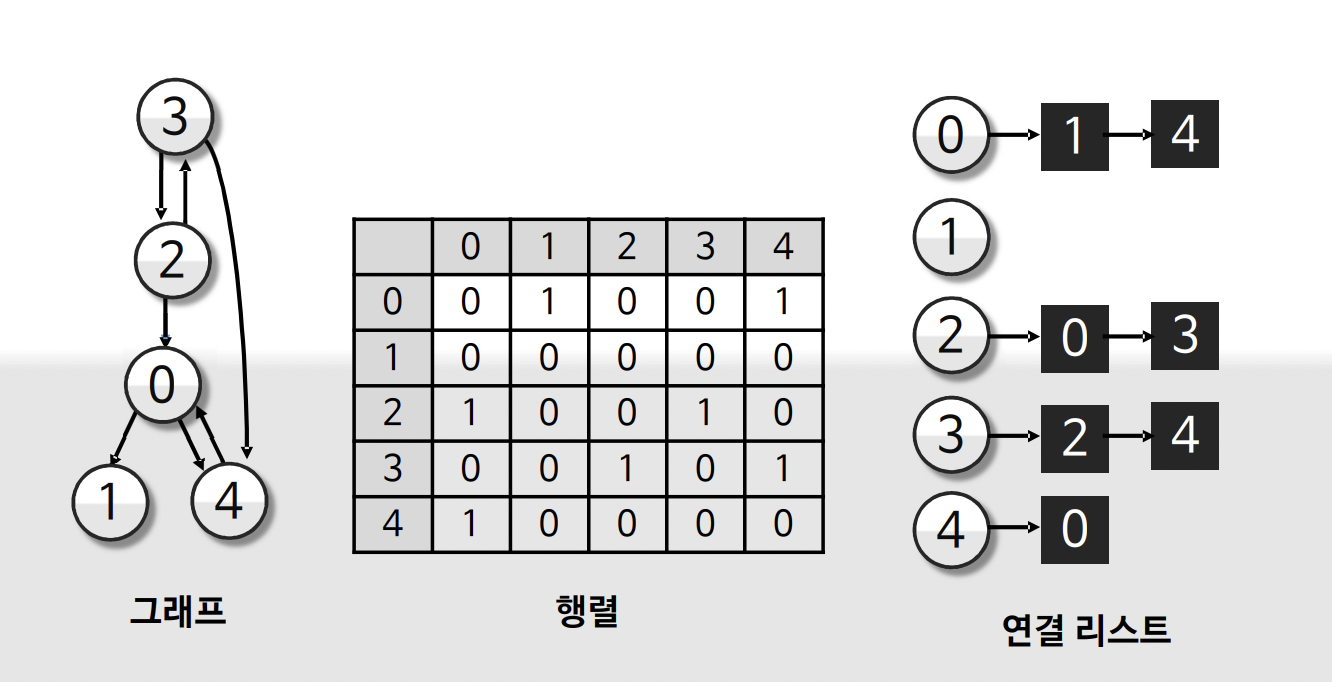
• dense graph(엣지의 개수가 많음)인 경우 2차원 배열 활용, sparse graph(엣지의 개수가 적음)인 경우 연결 리스트를 활용

그래프의 탐색 알고리즘

탐색 알고리즘

• 하나의 정점에서 시작하여 그래프의 모든 정점을 방문하는 알고리즘
• 트리의 순회와 비슷 → 트리보다 구조 복잡(트리는 계층 구조가 있기 때문에 더 간단)

DFS(Depth-First Search, 깊이 우선 탐색)

• 미로 찾기와 비슷. 시작점에서 가장 깊이 들어갈 수 있는 곳 까지 탐색한 후 길이 막히면 갈림길이 있었던 곳으로 다시 돌아와서 시작하는 형태

• 스택 또는 재귀 함수를 활용하여 구현

• 구현 방법(스택)

  1. 방문한 노드를 관리하는 배열과 스택 배열로 관리. 스택은 막다른 길에 도달했을 때 다시 되돌아오기 위해 사용.
  2. 먼저 시작점을 방문했다고 배열에 저장 후 해당 노드를 스택에 저장. 그 다음으로 이동한 노드에서 방문할 수 있는 노드가 있는지 확인 후 방문 가능하면 방문한 노드 배열에 저장하고 해당 노드를 스택 배열에 저장. 만약 방문할 수 있는 노드가 없는 경우 스택에서 해당 노드를 pop 하고, 이전 노드로 백트래킹함.
  3. 스택이 빌 때까지 2 과정을 반복한 후 스택이 비어 있으면 종료

BFS(Breath-First Search, 너비 우선 탐색)

• 동심원 모양으로 탐색함.

• 큐를 사용하여 구현

• 구현 방법

  1. 시작점을 큐에 넣고 시작.
  2. 시작점에서 인접한 노드들을 큐에 넣고 시작점은 deque 하고 방문 처리 함. 큐의 순서대로 하나씩 방문 처리 하며 deque함. 방문시에 아직 방문하지 않은 인접한 노드가 있으면 새로 큐에 넣음.
  3. 큐가 빌 때까지 2를 반복하고 큐가 비어 있으면 종료

• 활용 영역
  1. 검색 엔진의 크롤링
  2. 최단 거리 구하기
  3. 웹 사이트의 소셜 네트워크
  4. 추천 시스템
  5. GPS 네비게이션 시스템
  

DFS vs BFS

• 메모리 사용량 : DFS < BFS
  - BFS의 경우 인접한 노드들을 모두 큐에 담기 때문에 불필요한 메모리를 잡아 먹게 됨. 인접한 노드들을 모두 큐에 넣는 과정에서 오버플로우가 발생할 수 있음.
• 속도 : DFS < BFS
• 언제 무엇을 사용 해야 하는가?
  - DFS, BFS의 시간 복잡도는 같기 때문에 중 뭐가 더 낫다고 볼 순 없고 상황에 맞게 사용하면 됨.
  - 그래프의 모든 정점을 방문해야 한다면 BFS, DFS 둘 다 상관 없음
  - 그래프가 정말 크다면 DFS가 낫고 최단 거리 계신 시에는 BFS가 나음.
  - 경로의 특징을 저장하는 등의 로직이 더 필요한 경우 DFS 사용

출처

• 알고리즘과 문제해결 / 고려사이버대학교, 임철홍
• 알고리즘 / 인천대학교, 전경구
• https://www.geeksforgeeks.org/applications-of-breadth-first-traversal/