문제
문제 링크 - N-Queen
풀이
알고리즘
전제
- 먼저 N의 최대값(15) 크기의 int 배열 선언.
본 문제에서는 체스판 배열의 i번째 행, j번째 열을 visited[i][j]와 같은 2차원 배열이 아닌 1차원 배열 visited[i]=j 로 표현할 것.vector<int> visited(15);
- 백트래킹 문제이므로 DFS를 바탕으로 유망하지 않은 가지(노드)를 쳐내며, 유망한 가지들만 탐색함.
- N_Queen 함수를 재귀 탐색하되, Check 함수에서 유망한 가지들을 판별함.
N-Queen 문제 해결 조건
- 서로 다른 퀸은 같은 행 또는 같은 열에 위치할 수 없음.
따라서 한 행에 1개의 퀸, 한 열에 1개의 퀸만 존재함.- 서로 다른 퀸은 대각선상에 위치할 수 없음.
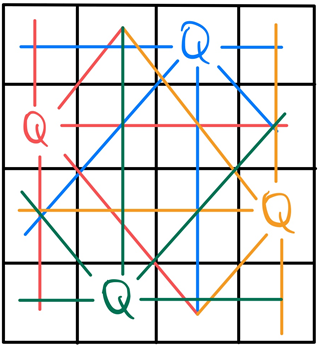
- 따라서 4*4 체스판에 4개의 퀸을 배치하기 위해서는 같은 행,열, 그리고 대각선상이 아니어야 하므로 아래와 같이 배치해 볼 수 있으며 현재 고려해야 할 조건은 표시된 선(퀸의 공격범위)과 같다.
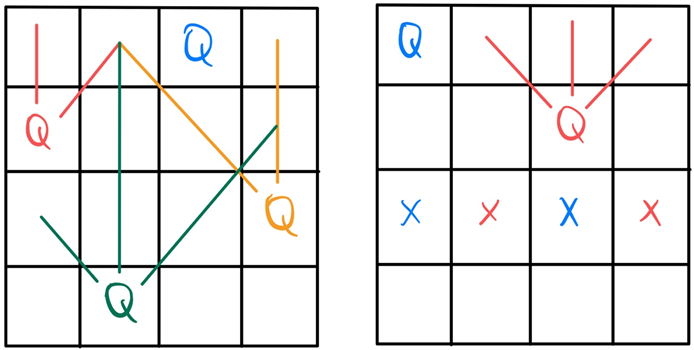
- 위 1번에서 한 행, 한 열에 1개의 퀸만 존재한다고 했으므로 체스판의 첫번째 칸(0,0)부터 첫번째 퀸(파란색)을 배치해보면서 (0,1), (0,2), (0,3) 까지 배치해본다면 아래와 같이 조건을 줄여볼 수 있다.
좌) 성공, 우) 실패- 결론적으로 해당 판단 조건을 통해 가지치기를 한 뒤 재귀적으로 퀸을 배치해보면 해답을 얻을 수 있음.
(3번까지의 조건으로도 해답은 구할 수 있지만 해당 문제에는 10초의 시간 제한이 있다.)
코드
#include <iostream>
#include <vector>
using namespace std;
int N;
int answer = 0;
vector<int> visited(15);
bool Check(int qCnt)
{
for (int i = 0; i < qCnt; i++)
if (visited[qCnt] == visited[i] || qCnt - i == abs(visited[qCnt] - visited[i]))
return 0;
return 1;
}
void N_Queen(int qCnt)
{
if (qCnt == N)
{
answer++;
return;
}
for (int j = 0; j < N; j++)
{
visited[qCnt] = j;
if (Check(qCnt))
N_Queen(qCnt + 1);
}
}
int main()
{
cin >> N;
N_Queen(0);
cout << answer;
}코드...인데 이제 주석을 첨가한...
#include <iostream>
#include <vector>
using namespace std;
int N; //입력: 1 ≤ N < 15
int answer = 0; //출력
//체스판 배열
vector<int> visited(15, -1);
// 유망한 조건 판단
// qCnt: 현재 배치한 퀸의 행
bool Check(int qCnt)
{
// 0번째 열부터 qCnt 열까지 반복
for (int i = 0; i < qCnt; i++)
{
// 배치했던 퀸들과 현재 배치하려는 퀸이 서로 공격할 수 있다면 return 0
// 세로축(열) 판단: 현재 배치한 퀸의 열 == 배치했던 퀸의 열 ||
// 대각축 판단: 현재 배치한 퀸의 행 - 배치했던 퀸의 행 ==
// 절대값(현재 배치한 퀸의 열 - 배치했던 퀸의 열)
if (visited[qCnt] == visited[i] || qCnt - i == abs(visited[qCnt] - visited[i]))
return 0;
}
//현재 퀸을 배치할 수 있다면 return 1
return 1;
}
void N_Queen(int qCnt)
{
// 현재 배치한 퀸의 갯수가 입력값(N)과 같다면 탈출
if (qCnt == N)
{
//출력(해답)++
answer++;
//케이스 테스트 출력
cout << "<case " << answer << ">\n";
for (int i = 0; i < visited.size(); i++)
{
if (visited[i] != -1)
cout << "[" << i << ", " << visited[i] << "]\n";
}
cout << "\n";
return;
}
// 0번째 행부터 N 행까지 반복
for (int j = 0; j < N; j++)
{
// [qCnt, j] 에 배치해보고
visited[qCnt] = j;
// 배치할 수 있다면
if (Check(qCnt))
// 퀸의 행을 + 1 하고 다음 퀸을 배치해본다.
N_Queen(qCnt + 1);
}
}
int main()
{
cin >> N;
N_Queen(0);
cout << "answer: " << answer;
}테스트 케이스 출력
input: 4
<case1>
[0, 1]
[1, 3]
[2, 0]
[3, 2]
<case2>
[0, 2]
[1, 0]
[2, 3]
[3, 1]
answer: 2초기 헤딩 및 여담
최근 푼 문제들 중에 해당 문제를 제일 오래 잡고있었다.
이유로는 첫째로 본인이 재귀적인 풀이에 너무 약하다는 것 때문.
둘째로는 N-Queen 문제는 상당히 유명하고 소위 '정해진 답'이 존재하는데 이런 것을 참고하지 않고 풀고 싶다는 생각이 커서 그 과정중에 상당히 오랫동안 헤딩을 하였다.(결과적으로는 N-Queen 문제를 제대로 공부한 후에 풀었으므로 여러분들은 헤딩을 너무 오랫동안 하지는 말자...)
아무튼 백준 단계별 풀기로 해당 문제를 접하게 되었다면 먼저 재귀적 풀이와 앞선 백트래킹 문제들에 상당히 익숙해질 필요가 있다. 이 문제가 해당 기법의 활용을 통해 푸는 대표적인 문제이므로 적당히 알면 풀기 힘들다.(필자처럼)
아래는 필자가 헤딩을 통해 최대한 최적화해봤던 코드이며 올바른 해답을 얻을 수 있다.(물론 시간초과로 틀렸다.)
기본적인 DFS 구조를 따르며 퀸을 일단 배치한 후에 Visit 함수를 통해 퀸과 퀸의 아래쪽 공격범위를 모두 '방문'한 것으로 해주며 재귀탐색 하였는데, 가장 큰 문제는 Visit의 계산량이 N이 커질수록 기하급수적으로 커진다는 점이다.(정석적 풀이는 N=8일 때 1s정도인 반면 아래는 3s 정도이다.)
둘째로는 2차원 배열을 사용했다는 점 정도이다. 사실 2차원 배열이 좀 더 직관적이라고 느껴지지만 해당 문제에서는 굳이 2차원 배열을 사용할 필요가 없다.
마지막으로 본 문제를 푼 후에 맞은 사람 순위를 보았는데 N을 입력받으면 미리 입력해둔 답안을 그저 출력만 하는... 어이없는 코드였다. 순위가 별로 의미가 없는 듯 하다. 프로그래머스같은 경우에는 다른 사람의 추천을 통해 추천수에 따라 코드를 정렬하여 보여주므로 도움을 받는 경우도 많은데 백준은 이런 부분이 좀 아쉽게 느껴진다.
필자의 초기 헤딩 코드
#include <iostream>
#include <vector>
using namespace std;
int N; // 1 ≤ N < 15
int answer = 0;
vector<vector<bool>> Visit(vector<vector<bool>> visited, int i, int j)
{
visited[i][j] = true;
for (int n = 1; i + n < N; n++)
{
visited[i + n][j] = true;
if (j + n < N)
visited[i + n][j + n] = true;
if (j - n >= 0)
visited[i + n][j - n] = true;
}
return visited;
}
void N_Queen(int qCnt, vector<vector<bool>> visited)
{
if (qCnt == N)
{
answer++;
return;
}
for (int j = 0; j < N; j++)
{
if (visited[qCnt][j])
continue;
N_Queen(qCnt + 1, Visit(visited, qCnt, j));
}
}
int main()
{
cin >> N;
vector<vector<bool>> visited(N, vector<bool>(N)); // N*N
N_Queen(0, visited);
cout << answer;
}