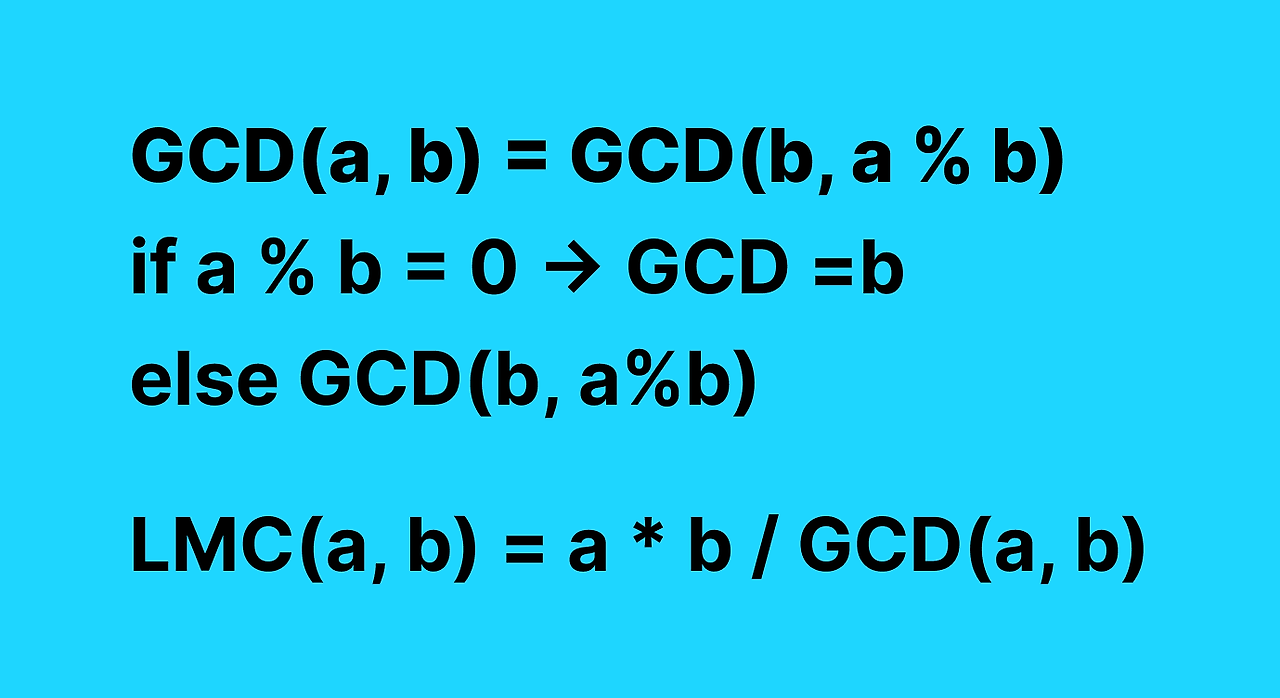
유클리드 호제법 - 최대 공약수, 최소 공배수 구하기(Python 코드)

Rachel·2024년 5월 20일

Algorithm

목록 보기

9/10

유클리드 호제법
2개의 자연수 또는 정식의 최대 공약수를 구하는 알고리즘의 하나.
2개의 자연수 a, b에 대해서 a를 b로 나눈 나머지를 r이라 하면(단, a > b), a와 b의 최대공약수는 b와 r의 최대공약수와 같다.

🌟 최대 공약수(The Greatest Common Denominator)

def gcd(a, b):
    while b > 0:
        a, b = b, a % b
    return a

숫자 a, b가 있을 때 계속해서 a에 b, b에 a%b를 대입시키고, b가 0될 때까지 반복하면 a와 b의 최대 공약수를 구할 수 있다.

python에서는 math 라이브러리에서 gcd를 제공한다.

🌟 최소 공배수(The Least Common Multiple)

def lcm(a, b):
    return a * b / gcd(a, b)

a*b 값을 gcd(a, b)로 나누면 최소 공배수를 구할 수 있다.

math.lcm 역시 제공

관련 문제

백준 1735번 분수 합

import sys
input = sys.stdin.readline

a, b = map(int, input().split())
c, d = map(int, input().split())

denominator = b * d
numerator = a * d + b * c

def gcd(a, b):
    while b > 0:
        a, b = b, a % b
    return a

GCD = gcd(numerator, denominator)

print(numerator//GCD, denominator//GCD)

분모: denominator
분자: numerator

유클리드 호제법을 이용하지 않으면 시간 초과가 발생한다.

백준 2485번 가로수

import sys
from math import gcd
input = sys.stdin.readline

N = int(input())

compare_tree = int(input())

arr = []

for _ in range(N-1):
    tree = int(input())
    arr.append(tree - compare_tree)
    compare_tree = tree
    
g = arr[0]
for i in range(len(arr)):
    g = gcd(g, arr[i])
    
result = 0
for x in arr:
    result += x // g - 1
print(result)