소수란?
소수는 약수가 1과 자신 밖에 없는 수를 의미하며 예를 들면 2,3,5,7,11 등이 있다
Ch1 소수의 종류
소수의 종류에는 두가지가 있다
1. 쌍둥이 소수
소수들 중 3과 5, 11과 13, 17과 19처럼 두 수의 차가 2인 소수를 쌍둥이 소수라고 한다
2.메르센 소수

프랑스의 한 수도사인 메르센의 이름을 따 만든 소수이다. 그는 소수를 간단하게 표현하려고 애써서 '2^p-1은 소수이다' 라는 논문을 발표하였지만 아니라는 것이 밝혀져 무쓸모가 됬지만. 현대에 들어서 2^p-1인 수들을 모아 메르센 소수라고 불려지게 되었다
Ch2 python으로 소수를 구하는 함수 만들기
코드:
def prime(n):
for i in range(2, int(n**(1/2))+1):
if n % i == 0:
return False
return True설명:
먼저 함수 이름을 설정해 준다
def prime(n):함수를 만드는 방법은 def 다음에 불렸으면 하는 글자를 넣어주면 된다
ex) def hi(n):
함수안에 반복문을 적어 숫자 n이 소수인지 아닌지 찾는다
for i in range(2, int(n**(1/2))+1):마지막으로 조건문과 결과를 출력하는 코드를 작성한다
if n % i == 0:
return False
return Truereturn True와 return False는 각각 True와 False를 출력한다는 의미를 가지고 있다
이 함수를 이용하여 N의 값을 받아 2부터 N까지 돌며 소수를 확인하는 코드를 만들어 보자
먼저 N을 입력 받는다
N = int(input())
def prime(n):
for i in range(2, int(n**(1/2))+1):
if n % i == 0:
return False
return True그 다음 반복문을 이용해 2부터 N까지의 수를 찾아 방금 만들었던 함수를 이용해 그중에서 소수들만 출력한다
N = int(input())
def prime(n):
for i in range(2, int(n**(1/2))+1):
if n % i == 0:
return False
return True
for x in range(2,N+1):
print(x,":",prime(x))Ch3 에라토스테네스의 체(in Python)
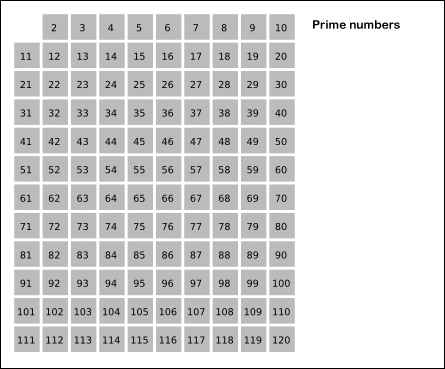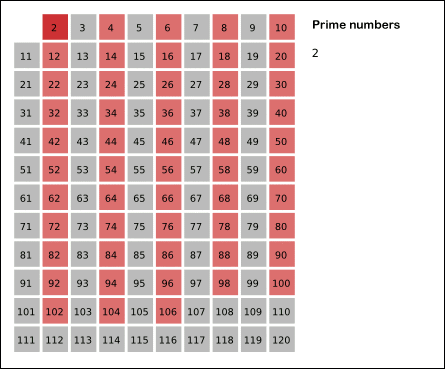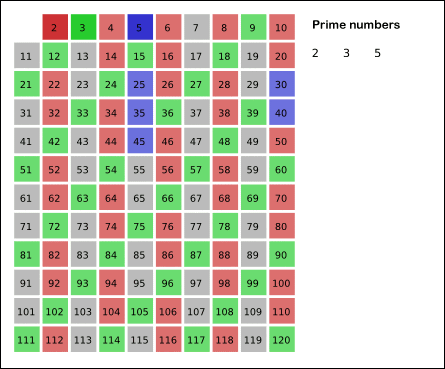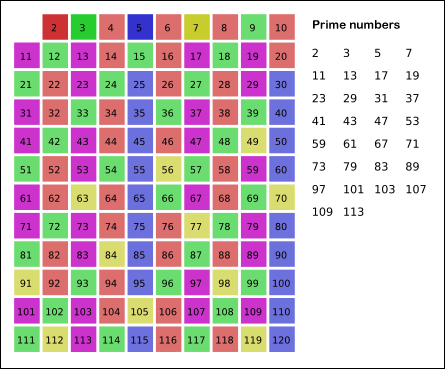
출처:위키피디아
에라토스테네스의 체의 원리:
1. 2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다. 그림에서 회색 사각형으로 두른 수들이 여기에 해당한다.
-
2는 소수이므로 오른쪽에 2를 쓴다. (빨간색)
-
자기 자신을 제외한 2의 배수를 모두 지운다.
-
남아있는 수 가운데 3은 소수이므로 오른쪽에 3을 쓴다. (초록색)
-
자기 자신을 제외한 3의 배수를 모두 지운다.
-
남아있는 수 가운데 5는 소수이므로 오른쪽에 5를 쓴다. (파란색)
-
자기 자신을 제외한 5의 배수를 모두 지운다.
-
남아있는 수 가운데 7은 소수이므로 오른쪽에 7을 쓴다. (노란색)
-
자기 자신을 제외한 7의 배수를 모두 지운다.
-
위의 과정을 반복하면 구하는 구간의 모든 소수가 남는다.
코드:
def prime_list(n):
# 전체 수를 담은 리스트 만들기
sieve = [True]*(n+1)
for i in range(2, int(N**(1/2))+1):
if sieve[i] == True:
for j in range(i*2, n+1, i):
sieve[j] = False
prime_number = []
for i in range(2,n+1):
if sieve[i]:
prime_number.append(i)
return prime_number
설명:
코드가 매우 길기에 간략하게 설명하면 N+1 개의 True가 담긴 리스트를 만들고
0과 1은 False로 만든다. 그리고 리스트를 처음부터 끝까지 반복하는데,
그 다음부터 True인 수를 만나면 그 수 외 배수들을 전부 False로 바꾼다.
이 이상 소수에 관한 것들이었다


ㅎㅇ