[프로그래머스] 최대공약수와 최소공배수-JAVA

말하는 감자·2022년 5월 10일

Programmers Level 1

목록 보기

8/66

프로그래머스 Level 1

🔒 최대공약수와 최소공배수

📚 문제 설명

두 수를 입력받아 두 수의 최대공약수와 최소공배수를 반환하는 함수, solution을 완성해 보세요. 배열의 맨 앞에 최대공약수, 그다음 최소공배수를 넣어 반환하면 됩니다. 예를 들어 두 수 3, 12의 최대공약수는 3, 최소공배수는 12이므로 solution(3, 12)는 [3, 12]를 반환해야 합니다.

✅ 제한 사항

두 수는 1이상 1000000이하의 자연수입니다.

📖 입출력 예

n	m	result
3	12	[3, 12]
2	5	[1, 10]

📃 입출력 예 설명

입출력 예 #1
위의 설명과 같습니다.

입출력 예 #2
자연수 2와 5의 최대공약수는 1, 최소공배수는 10이므로 [1, 10]을 리턴해야 합니다.

🗝️ 작성 코드

class Solution {
    // 최대공약수 구하는 함수 (유클리드 호제법)
    int gcd(int n, int m) {
        int r;
        while(m > 0) {
            r = n % m;
            n = m;
            m = r;
        }
        return n;
    }
    
    public int[] solution(int n, int m) {
        int[] answer = new int[2];

        // 두 수에서 더 큰 수를 n으로 지정
        if(n < m) {
            int temp = n;
            n = m;
            m = temp;
        }
        
        // 최대공약수 구하기
        answer[0] = gcd(n, m);
        
        // 최소공배수 구하기
        answer[1] = n * m / answer[0];
        
        return answer;
    }
}

최대공약수는 유클리드 호제법을 이용해 구하고
최소공배수는 n*m/최대공약수 임을 활용하여 구한다.

최대공약수는 유클리드 호제법을 이해해야 풀 수 있었는데

~~감자는 모르겠다...~~

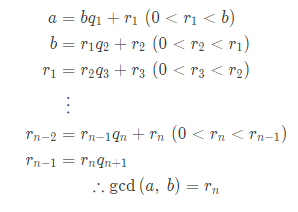
a는 나눠지는 수 / b는 나누는 수 / r은 나머지

음... 그러니깐... 나머지를 나누는 수에 계속 나누면 마지막 나누는 수가 최대공약수라는 거지...?

하고 일단 냅다 구현했는데 맞았다!

유클리드 호제법은 gcd 함수에서 구현하였다.
처음에는 main 클래스 내에서 구하려고 했으나 n과 m을 따로 저장하거나 미리 곱해서 보관해야 할 것 같은데 헷갈릴 것 같아서 함수로 구현했다.

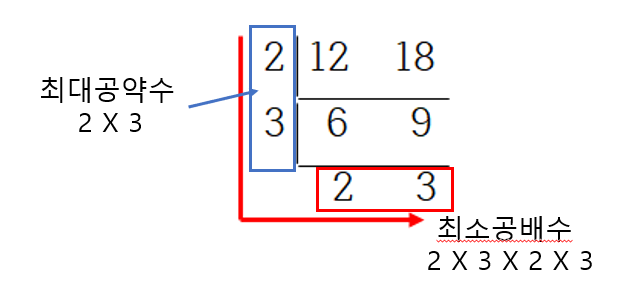
최소공배수는 두 수의 최대공약수 X 두 수의 나머지들 을 하면 나온다.
n X m을 하면 최대공약수 X 최대공약수 X 두 수의 나머지이므로 n X m / 최대공약수로 구할 수 있다.

🔓 다른 사람의 코드

import java.util.Arrays;

class TryHelloWorld {
    public int[] gcdlcm(int a, int b) {
        int[] answer = new int[2];

          answer[0] = gcd(a,b);
        answer[1] = (a*b)/answer[0];
        return answer;
    }

   public static int gcd(int p, int q)
   {
    if (q == 0) return p;
    return gcd(q, p%q);
   }

    // 아래는 테스트로 출력해 보기 위한 코드입니다.
    public static void main(String[] args) {
        TryHelloWorld c = new TryHelloWorld();
        System.out.println(Arrays.toString(c.gcdlcm(3, 12)));
    }
}