[Algorithm] 백준 1389 - 케빈 베이컨의 6단계 법칙 in Python(파이썬)

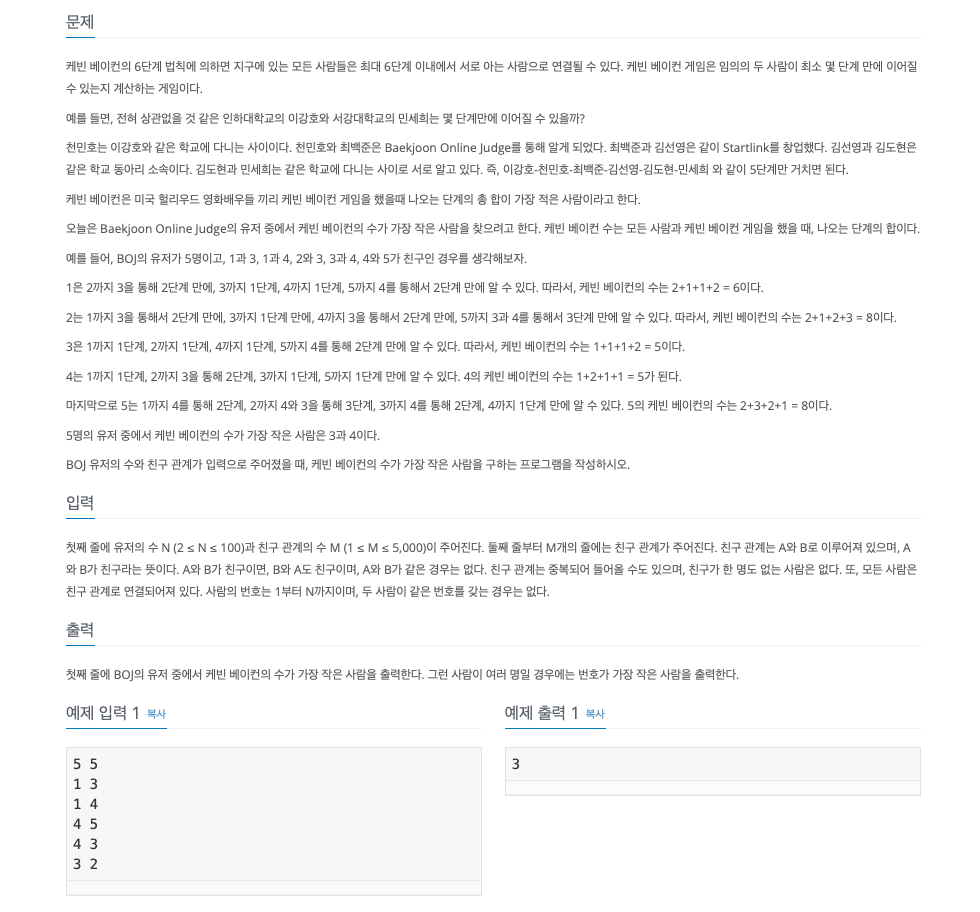
💡 백준 7576:

BFS 탐색을 통해 케빈 베이컨의 6단계 법칙 최소 관계 거리 탐색

🌱 코드 in Python

알고리즘: BFS

import sys

input = sys.stdin.readline
n, m = map(int, input().split())
g = [[] for _ in range(n + 1)]
for _ in range(m):
	a, b = map(int, input().split())
	g[a].append(b)
	g[b].append(a)

def bfs(i):
	visit = [-1] * (n + 1) # 자기 자신을 탐색하지 않도록 하기 위해 -1로 초기화
	visit[i] = 0 # 자기 자신은 0으로 초기화
	q = []
	q.append(i)
	while q:
		j = q.pop(0)
		for k in g[j]:
			if visit[k] == -1: # -1일 경우에만 탐색
				visit[k] = visit[j] + 1 # 자신까지 오기까지의 관계 거리 갱신
				q.append(k)
	return sum(visit[1:n + 1]) # 0번째 인덱스에 0이 있으므로 1부터 n까지 합

min_c = n * m # 임의이 최솟값 설정
ret = 0
for i in range(1, n + 1):
	tmp = bfs(i)
	if min_c > tmp: # 최소 거리 갱신
		ret = i # 1부터 차례대로 갱신되어 같은 최솟값이 있을 때 번호가 작은 사람이 답이 될 수 있음
		min_c = tmp
print(ret)

이 문제는 토마토 케빈 베이컨의 수가 가장 작은 사람을 구하는 문제였다
케빈 베이컨 수는 몇 다리 건너면 다 아는 사람이야~의 유식한 버전이랄까.

최소는 뭐다? bfs다~ 해서 풀었는데 플루이드 알고리즘을 쓰면 좀 더 좋다고 한다
지금 같은 경우는 간선에 가중치가 없어서 bfs로 풀어도 가능하지만, 가중치가 있을 때는 플루이드 알고리즘을 써야 한다고 한다.

자료구조 공부할 때 분명히 본 알고리즘인데 전혀 기억이 안나죠..?
빨리 복습해야 할 듯 ㅠㅠ

무난히 풀 수 있는 문제였다!

🧠 기억하자

1. 플루이드 알고리즘을 다시 공부하자!

백준 1389 바로가기