[Algorithm] 백준 1010: 다리 놓기 in Python(파이썬)

💡 백준 1010: 다리 놓기

강 동쪽이 항상 강 서쪽보다 크거나 같으므로 강동C강서 조합의 개수를 출력

👀 참고: 조합 배열 (mCn)

n \ m	1	2	3	4	5	6	7	8	9	...
1	1	2	3	4	5	6	7	8	9	...
2		1	3	6	10	15	21	28	36	...
3			1	4	10	20	35	56	84	...
4				1	5	15	35	70	126	...
5					1	6	21	56	126	...
...						1	...	...	...	...

🌱 코드 in Python

알고리즘: Dynamic Programing

import sys

t = int(sys.stdin.readline())
dp = [[0] * 30 for i in range(30)] # [30][30] 크기의 2차원 배열 생성
for i in range(30):
	for j in range(30):
		if i == 1: # mC1의 경우 m개의 조합이 가능
			dp[i][j] = j
		elif i == j: # mCm의 경우 1개의 조합이 가능
			dp[i][j] = 1
		elif i < j: # mCn (n < m)의 경우 [n - 1][m - 1] + [n][m - 1]개의 조합이 가능
			dp[i][j] = dp[i - 1][j - 1] + dp[i][j - 1]
for i in range(t):
	n, m = map(int, sys.stdin.readline().split())
	print(dp[n][m])

주어진 n, m에 대한 mCn의 값을 구하는 문제로 풀이 방법이 꽤 다양한 문제였다

상기 코드는 입력값이 30을 넘지 않으므로 dp를 활용하여 조합의 개수를 2차원 배열로 먼저 모두 구해 놓은 후,
그 배열에 해당하는 값을 출력하는 식으로 구현하였다

위의 참고를 보면 조합 개수의 규칙을 알 수 있어 그대로 배열을 구현할 수 있다

import sys

for i in range(t):
	n, m = map(int, sys.stdin.readline().split())
	ret = 1
	k = m - n
	while m > k:
		ret *= m
		m -= 1
	while n > 1:
		ret = ret // n
		n -= 1
	print(ret)

🍄 다음으로는 순열을 구하는 아래의 공식을 활용한 산술 계산 방법이다

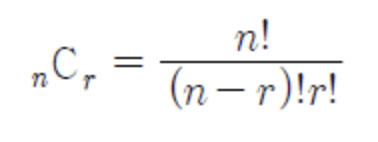
mCn = m! / (m - n)!n! 이다 따라서
분모: m x (m - 1) x ... x ((m - n) x (m - n - 1) x ... x 1)
분자: ((m - n) x (m - n - 1) x ... x 1) x n x (n - 1) x ... x 1

이때 분모의 (m - n)!과 분자의 (m - n)! 부분은 동일하여 나눠서 사라지고, 분모는 m (m - 1) ... (m - n + 1), 분자는 n (n - 1) ... 1 부분만 남게 된다
따라서 m 부터 m - n 전 까지의 팩토리얼을 n!로 나눈 값이 결과가 된다

import sys, math

for i in range(t):
	n, m = map(int, sys.stdin.readline().split())
	print(math.comb(m, n))

🍄 그 외에도 여러 방법이 있겠지만 내가 구해본 마지막 방법으로는 파이썬 math 모듈에서 제공하는 comb 함수를 이용하는 것이다
이게 사실 제일 깔끔하고 내가 직접 해야할 일도 적어서 가장 간편한 방법이긴 하다!

각각의 시간은 백준 테스트 케이스 기준으로 1번 64ms, 2번 68ms, 3번 68ms가 걸렸다

---

🧠 기억하자

이번 문제는 각각의 조합마다 dp를 활용할 수 있는 규칙이 있는 줄 알고 한참을 헤매다가...
결국 검색을 통해서 해결했다. 또르륵.

DP로 이 문제를 풀려면 각각의 조합이 아니라, 조합들이 어떤 규칙성을 가지는 지 파악한 2차원 배열을 만드는 것이 핵심이었다

그 외에 다른 방법들은 DP가 아니라 조합 그 자체의 계산에 집중한 것들인데,
아 저 수포자라고요,, 흑흑 ㅠㅠ 오랜만에 조합 문제를 풀어본 것 같다
공기업 다닐때 ncs공부하며 조합풀던 때도 몇년전인디,, 참나,,

아무튼! 이런 방법도 있다는 것을 여러 갈래로 알아본 것에 의의를 둘 수 있을 것 같다
다음번에 조합 문제가 나오면 내가 바로 풀 수 있지!! 암!!

백준 1010 바로가기