💡 백준 1309: 동물원
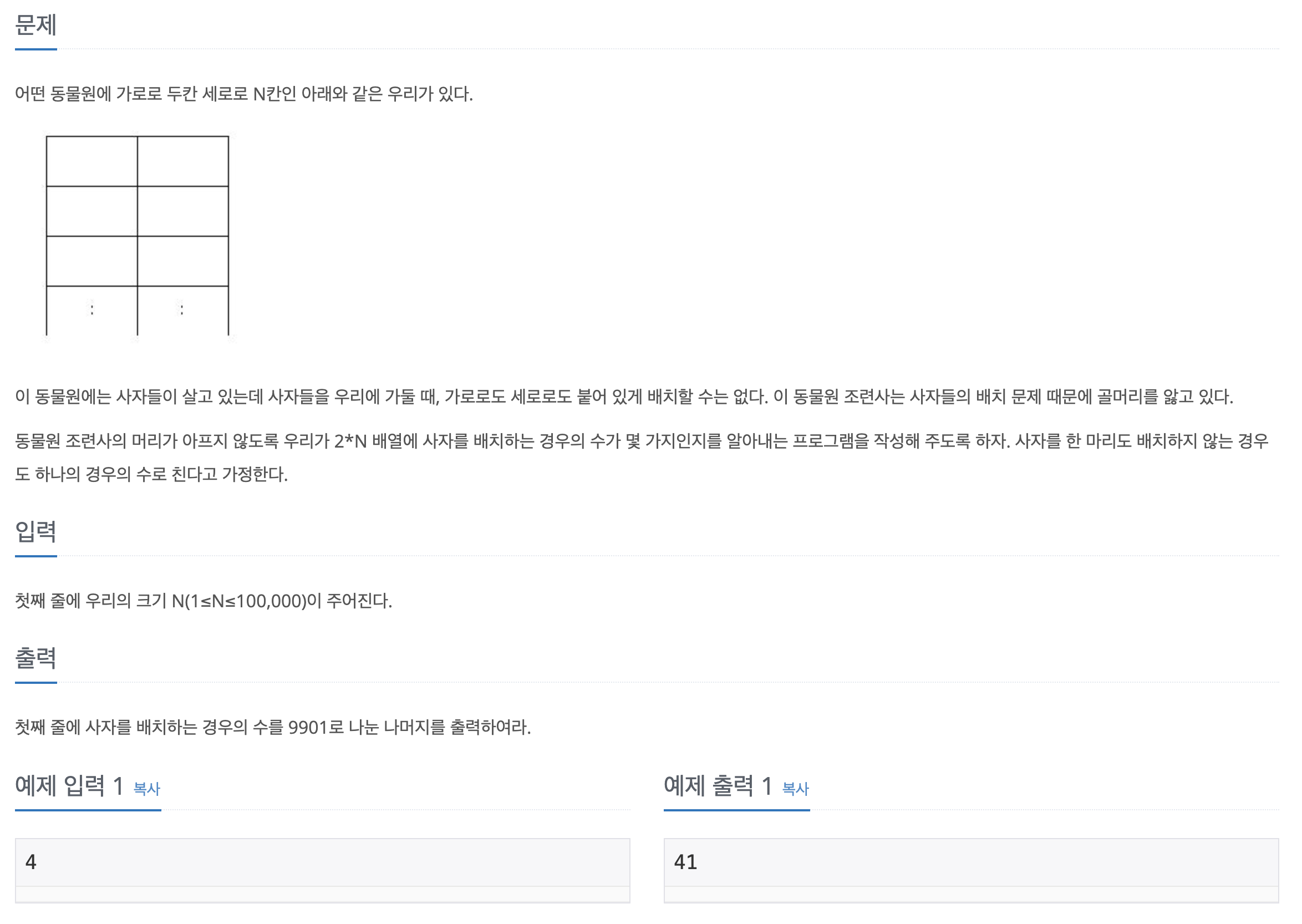
사자를 배치할 수 있는 기본형 3가지에서 파생되는 규칙을 찾아 DP배열로 만든 후 DP[n] 출력
🌱 코드 in Python
알고리즘: Dynamic Programing
import sys
n = int(sys.stdin.readline())
dp = [0, 3, 7]
for i in range(3, n + 1):
dp.append((dp[i - 2] + (dp[i - 1] * 2)) % 9901)
print(dp[n])사자를 채울 때 가장 기본 배열은 아래와 같이 3가지로 나눌 수 있다
1) 사자를 배치하지 않는 경우
| x | x |
|---|
2) 사자를 왼쪽에 배치하는 경우
| o | x |
|---|
3) 사자를 오른쪽에 배치하는 경우
| x | o |
|---|
모든 사자 배열은 위 3가지 경우로 끝난다
4) 각각에 대하여 1) 다음줄에는 1), 2), 3)이 다 가능하여 1)로 끝나는 배열은 밑에 3가지 경우를 추가할 수 있다
5) 2) 다음줄에는 1), 3)만 가능하며, 3) 다음줄에는 1), 2)만 가능하다 따라서 1)이 아닌 나머지 경우는 모두 2), 3)으로 끝날 것이기 때문에 그 모든 경우에 대하여 *2가지 경우를 추가할 수 있다
6) N은 N - 2의 결과에 1)을 한 줄 추가한 것에 대하여 4)에 대입하여 N - 2 x 3의 확장이 발생할 수 있다
7) 또한, N - 1의 결과 중 N - 2에 1)을 한 줄 추가한 것을 제외한 모든 경우는 2) 혹은 3)으로 끝나는 경우이기 때문에 {(N - 1) - (N - 2)} x 2의 확장이 발생할 수 있다
여기서 도출할 수 있는 계산식은 DP[N] = (DP[N - 2] x 3) + {(DP[N - 1] - DP[N - 2]) x 2)이며,
이를 정리하면 DP[N] = DP[N - 2] + {(DP[N - 1] - DP[N - 2]) x 2)가 되는 것이다
이때 DP[1] = 3(기본형 3가지), DP[2] = 7까지 구해놓고 DP를 시작한다
그림으로 보면 아래와 같다

나는 이 이상은 설명을 몬하겠다.. 흑 ㅠㅠ
또 여기서 주의할 점은 입력이 100,000까지 들어올 수 있기 때문에 * 2 와 같은 부분에서 메모리 초과가 날 수 있으므로
매 계산마다 % 9,901 계산을 해주어야 한다
🧠 기억하자
실버 문제인데 이렇게 어려우면 어떡하지?
나는 골드 언제 풀어보지?
이것도 내가 못풀었다 하하
일단 이해한 것에 의의를..
다음에는 내가 꼭 규칙 찾기,, 약속,,
아 그리고 입력값에 대한 주의를 꼭 해야 할 것 같다
왜 답에서 9,901로 나눈 나머지를 구하라고 했겠는가?
생각하자 생각!

