💡 백준 2206:
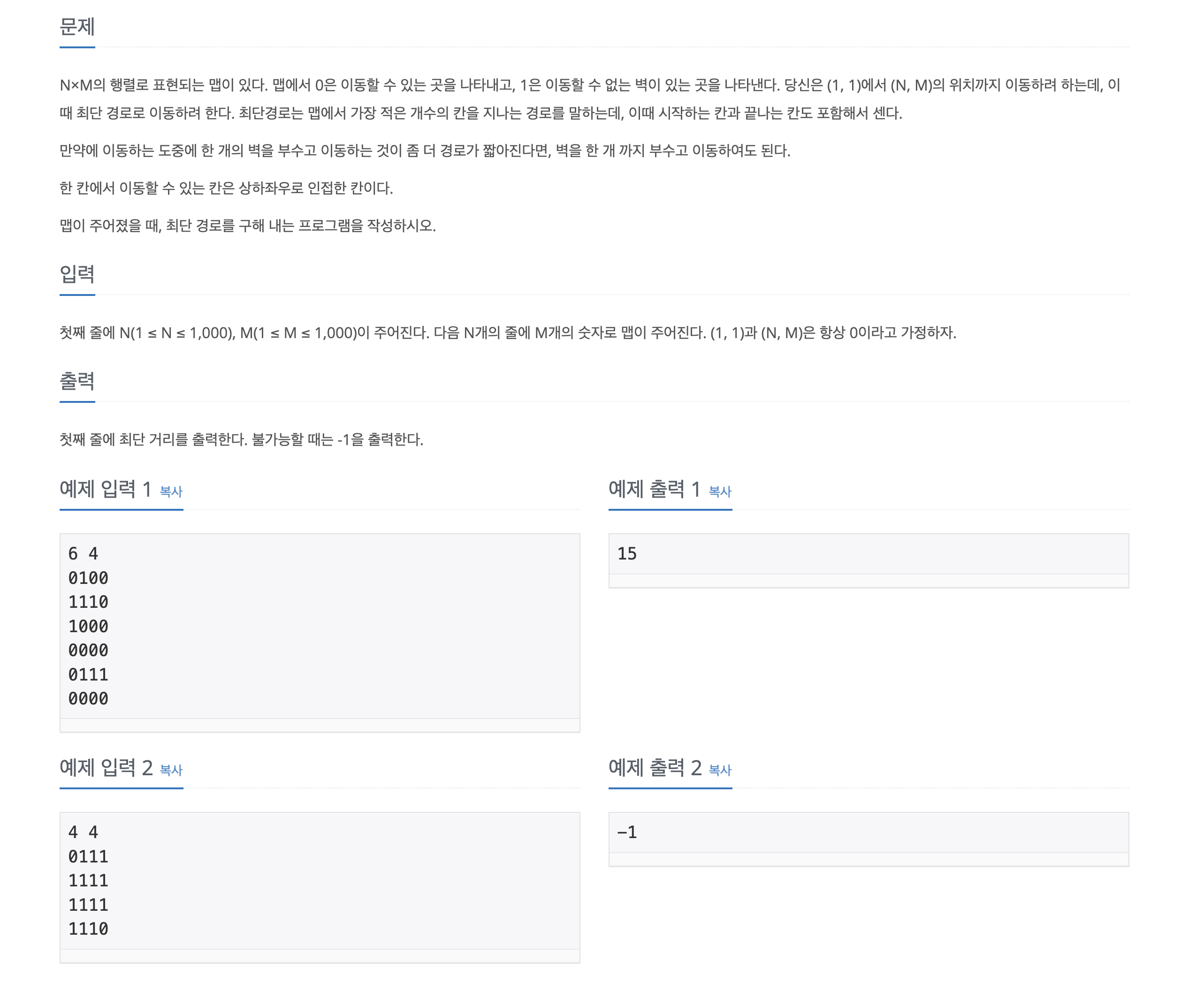
BFS로 순회하며 최단거리 탐색
🌱 코드 in Python
알고리즘: BFS
import sys
from collections import deque
input = sys.stdin.readline
x = [1, 0, -1, 0]
y = [0, -1, 0, 1]
def bfs():
q = deque()
q.append([0, 0, 1])
visit = [[[0] * 2 for _ in range(m)] for _ in range(n)]
visit[0][0][1] = 1
while q:
cx, cy, w = q.popleft()
if cx == n - 1 and cy == m - 1:
return visit[cx][cy][w]
for dx, dy in zip(x, y):
nx = cx + dx
ny = cy + dy
if 0 <= nx < n and 0 <= ny < m:
if s[nx][ny] == 1 and w == 1: # 벽이지만 뚫고 지나갈 수 있을 때
visit[nx][ny][0] = visit[cx][cy][1] + 1 # 벽을 뚫지 않은 전 단계의 최소 거리에 + 1
q.append([nx, ny, 0]) # 벽을 뚫고 지나간 적이 있음을 표시
elif s[nx][ny] == 0 and visit[nx][ny][w] == 0: # 벽이 아니고 아직 방문한 적 없는 곳일 때
visit[nx][ny][w] = visit[cx][cy][w] + 1 # 전 단계가 벽을 뚫고 온 것인지 아닌지 모르기 때문에 그에 알맞게 벽정보와 함께 거리 갱신
q.append([nx, ny, w])
return -1
n, m = map(int, input().split())
s = []
for i in range(n):
s.append(list(map(int, list(input().strip()))))
print(bfs())이번 문제는 골드문제 답게 ^^ 정말 정말 고생했다 하..
처음 문제를 보고 오 최소 거리니까 무조건 bfs!!! 까지는 순조로웠다
근데 그 다음 조건이 문제였다
벽을.. 한 번은... 뚫을 수 있다,,,?????
이게 무슨 경우의 수야,, 어이없어 정말...
그래서 내가 생각한 건... 모든 벽의 개수를 확인해서 하나씩 뚫어가며 최소 거리를 각 경우의 수마다 찾는 방법이어따 ^-^!
입력이 1000 x 1000이었기 때문에 당.연.히 시간초과가 날 것 같았지만,
일단 문제를 해결할 수나 있나 보자!! 해서 그대로 풀어봤다
import sys
from collections import deque
input = sys.stdin.readline
path = []
n, m = map(int, input().split())
cnt = 1
for i in range(n):
path.append(list(map(int, list(input().strip()))))
cnt += path[i].count(1)
if n == 1 and m == 1 and path[0][0] == 0:
print(0)
else:
prev = (0, 0)
ret = []
x = [1, 0, -1, 0]
y = [0, -1, 0, 1]
def bfs(c_x, c_y):
q = deque()
q.append((c_x, c_y))
visit[c_y][c_x] += 1
while q:
c_x, c_y = q.popleft()
if c_x == m - 1 and c_y == n - 1:
ret.append(visit[c_y][c_x] + 1)
return
for dx, dy in zip(x, y):
nx = c_x + dx
ny = c_y + dy
if 0 <= nx < m and 0 <= ny < n and visit[ny][nx] == -1 and path[ny][nx] == 0:
q.append((nx, ny))
visit[ny][nx] = visit[c_y][c_x] + 1
ret.append(-1)
def change_path(prev, cnt):
prev_y = prev[0]
prev_x = prev[1]
for i in range(prev_y, n):
for j in range(prev_x, m):
if path[i][j] == 1:
path[i][j] = 0
if cnt != 0:
path[prev[0]][prev[1]] = 1
return ((i, j))
prev_x = 0
prev = (0, 0)
for i in range(cnt):
visit = [[-1] * m for _ in range(n)]
bfs(0, 0)
prev = change_path(prev, i)
if max(ret) != -1:
min_ret = max(ret)
for i in ret:
if i < min_ret and i != -1:
min_ret = i
print(min_ret)
else:
print(-1)그러면 이런 누더기 같은 코드가 탄생한다 ^0^
아이 신나.
...
ㅠ
그래서 찾아보니 위 코드처럼 visit배열을 3차원으로 만들어서 벽을 뚫고 지나간 경우와 아닌 경우를 나누어
각각의 최소거리를 저장해주고 있었다
나참.. 이런 생각은 외못헤...
근데 사실 정답코드 보고도 아니 벽 딱 한개만 뚫어야 하는데 이게 돼????? 했다가
if s[nx][ny] == 1 and 2 == 1:
visit[nx][ny][0] = visit[cx][cy][1] + 1이 부분 보면서 정말 박수를 쳤다
와... 만약 벽을 뚫는 경우의 최단 거리를 저장할 경우엔 벽을 뚫지 않은 경우의 최단 거리를 더해주면 되는 거여따
그리고 벽이 아닌 경우에도 그 최단 거리가 이미 벽을 뚫고 온 경우의 최단거리인지, 아닌지 구별하기 위해
전 단계의 벽 상태를 같이 저장한다
실로 천재가 아닐 수 없다
어떻게 이런 생각을..?
솔직히 말해서 그 마지막의 elif 부분에 내가 벽이 아니고 나의 전 단계가 벽을 뚫고 지나간 경우와 아닌 경우를
다 나타낼 수 있나?! 하고 마지막까지 이해가 안돼서 그림을 다 그려본 나로서는..
일단은 이런 문제를 많이 접해봐야 나중에 또 이런 문제를 만났을 때 풀 수 있을 거 같다..
내 머리로는 어려워 ㅠㅠ
🧠 기억하자
- 한 줄로 된 숫자 배열을 이차원 배열로 append하는 방법
- s.append(list(map(int, list(input().strip()))))
- 처음에 list(map(int, input())) 이렇게만 했더니 0001 이런값을 다 1 이런식으로 정수로 치환되어 올바른 값을 입력할 수 없었다. 따라서 문자열로 리스트를 받은후에 그걸 다시 인트로 치환하여 map으로 쪼개논 걸 다시 list로 묶어줘야 한다- 아이고 어려워
- s.append(list(map(int, list(input().strip()))))
- 최소 거리에 조건이 있을 경우 조건까지 n차원 배열을 만들자!

