💡 백준 7562:
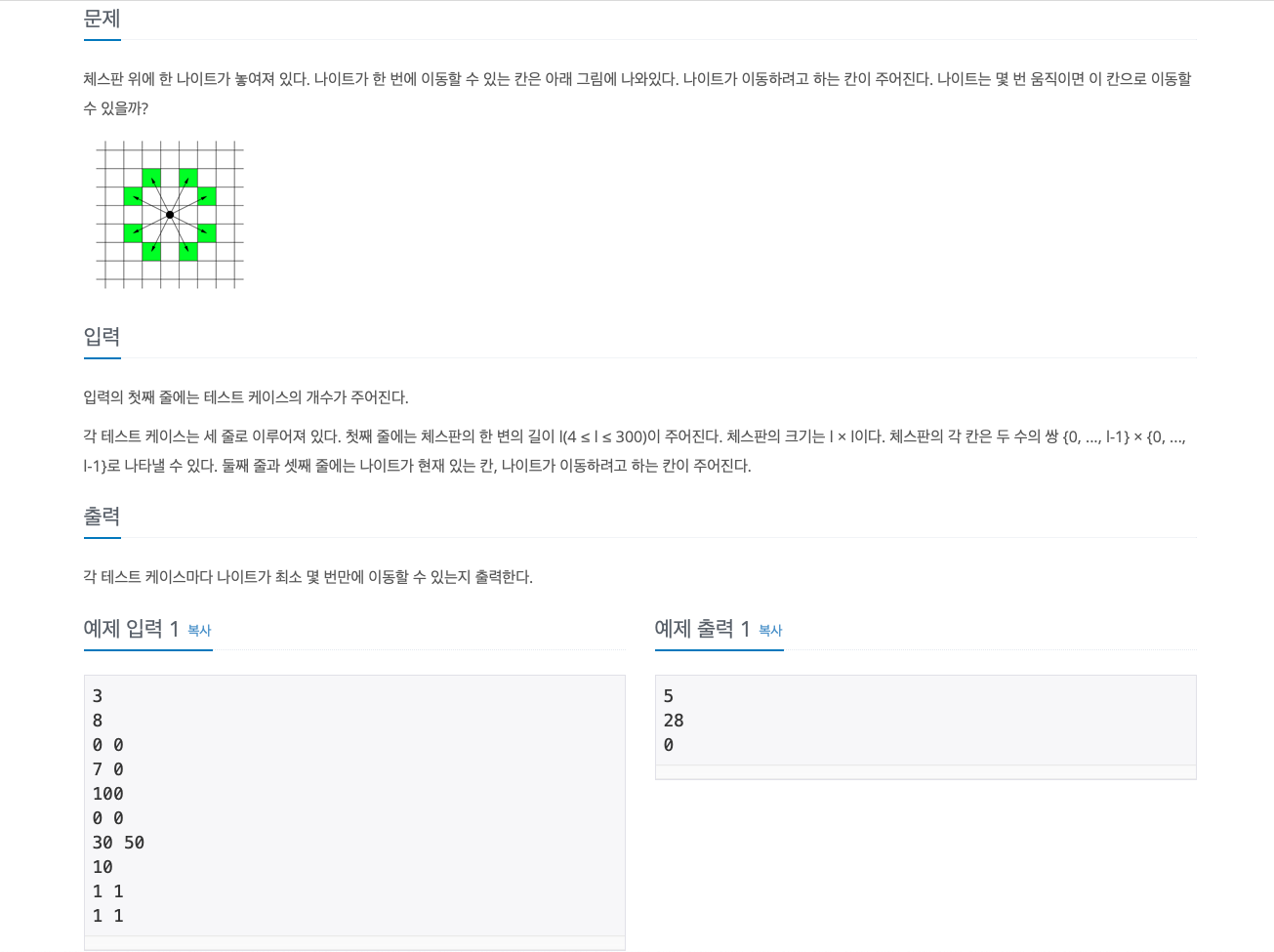
BFS로 순회하며 최단거리 탐색
🌱 코드 in Python
알고리즘: BFS
import sys
input = sys.stdin.readline
t = int(input())
x = [1, -1, 1, -1, 2, -2, 2, -2] # 이동 가능 x 배열
y = [2, 2, -2, -2, 1, 1, -1, -1] # 이동 가능 y 배열
def bfs(c_x, c_y):
q = []
q.append((c_x, c_y)) # 첫 시작 지점 큐 삽입
c[c_x][c_y] += 1 # 첫 좌표 거리 0으로 세팅
while q:
c_x, c_y = q.pop(0)
if c_x == e_x and c_y == e_y: # 정답을 찾았을 경우 while문 종료
return c[c_x][c_y]
for dx, dy in zip(x, y): # zip을 활용하여 두 iterable 객체 한 번에 반복
nx = c_x + dx # 다음 탐색할 x 좌표
ny = c_y + dy # 다음 탐색할 y 좌표
if 0 <= nx < size and 0 <= ny < size and c[nx][ny] == -1: # x, y 좌표가 탐색이 가능한 위치에 있고, 아직 방문하지 않은 곳일 경우
q.append((nx, ny)) # 큐에 삽입하여 탐색
c[nx][ny] = c[c_x][c_y] + 1 # 거리 갱신
for _ in range(t):
size = int(input())
c = [[-1] * size for _ in range(size)]
s_x, s_y = map(int, input().split())
e_x, e_y = map(int, input().split())
print(bfs(s_x, s_y))이번 문제는 첫 좌표에서 목표 좌표까지의 최소 이동 횟수를 세는 문제였다
앞서 풀었던 유기농 배추나 바이러스 등에서
1) 거리를 구할 때 방문 배열을 -1로 둔 상태에서 늘려가는 방법과
2) x = [-1, 1, 0, 0]과 같이 이동 방향에 대한 배열을 먼저 만들어 놓는 방법을 보았기 때문에
이를 응용하면 아주 빠르게 문제를 해결할 수 있을거라 생각했다
그치만 그건 경기도 오산이었고.. 참나.. 나는 이 문제를 보자마자 이거 촌수계산이랑 엄청 비슷하쟈낭,, dfs 풀어야 빠르겠다 왜냐? 계속 큐에 넣었다 뺐다 하는 것보다 그냥 비교하는게 빠르니까~~
라고 진심 똥멍청이 같은 생각을 했었던 것이다
여기서 중요한 건! 촌수계산 문제의 경우 자식은 딱 한 명의 부모밖에 가지고 있지 않기 때문에 해당 목표 지점으로 가는 길이 딱 하나다!
그래서 BFS를 쓰건 DFS를 쓰건 이동 거리의 수가 같을 수밖에 없었다
하우에버! 이번 문제의 경우 '최소' 거리를 구하는 것이 핵심 포인트고!
그 말은 목표 지점까지의 길이 여러 갈래가 있을 수 있다는 뜻이다!
따라서 dfs의 경우
알고리즘: dFS
import sys
input = sys.stdin.readline
t = int(input())
sys.setrecursionlimit(10**6)
x = [1, -1, 1, -1, 2, -2, 2, -2]
y = [2, 2, -2, -2, 1, 1, -1, -1]
def dfs(cur_x, cur_y):
for dx, dy in zip(x, y):
nx = cur_x + dx
ny = cur_y + dy
if nx == e_x and ny == e_y:
if c[e_x][e_y] == -1 or c[e_x][e_y] > c[cur_x][cur_y] + 1: # 현재 이동 경로가 전의 이동 경로보다 작을 경우 최소 거리로 갱신
c[e_x][e_y] = c[cur_x][cur_y] + 1
break
if 0 <= nx < size and 0 <= ny < size and (c[nx][ny] == -1 or c[nx][ny] > c[cur_x][cur_y] + 1):
c[nx][ny] = c[cur_x][cur_y] + 1
dfs(nx, ny)
for _ in range(t):
size = int(input())
c = [[-1] * size for _ in range(size)]
s_x, s_y = map(int, input().split())
e_x, e_y = map(int, input().split())
if s_x == e_x and s_y and e_y:
print(0)
continue
c[s_x][s_y] = 0
dfs(s_x, s_y)
print(c[e_x][e_y])위 코드와 같이 항상 비교하며 최소 거리를 갱신해줘야 하는 것이다
🔥 다시 말해!
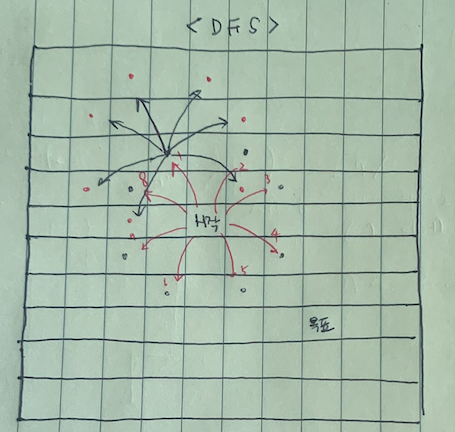
dfs는 위 그림처럼 방문한 정점의 모든 방위를 탐색하며 목표지점까지의 모든 경우의 수를 다 구해야 최소 거리를 알 수 있다
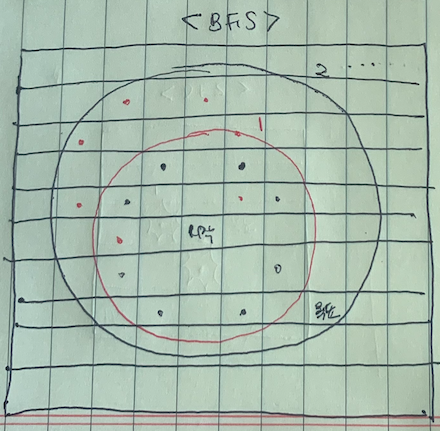
반면에 bfs는 같은 이동거리에 있는 정점들을 모두 조사한 후 그 중에 한 정점이라도 목표지점에 닿으면 그때 즉시 탐색을 종료할 수 있다!
그게 바로 최소거리라는 거지!!!!
하.. 힘들게 별로 없는데 스스로 힘들어진 문제였다 ㅠ
오늘 또 배웠다 ㅠㅠ
🧠 기억하자
- zip(iterator)
- 슬랙에 누가 파이썬 무겁게 찍먹하기 자료를 올려줬는데 거기서 보고 방법을 하나 얻었다
- 그냥 배열을 두고
for i in range(8): nx = c_x + d[i]해도 되긴 한다 - 근데 새로운 방법 하나 알아두면 좋잖아?
- 최소 거리!!!! 최단 거리!!
- bfs와 dfs의 특성을 다시 한 번 잘 생각하자
- dfs는 재귀를 돈다 최소와는 거리가 멀다

