💡 백준 9613: GCD 합
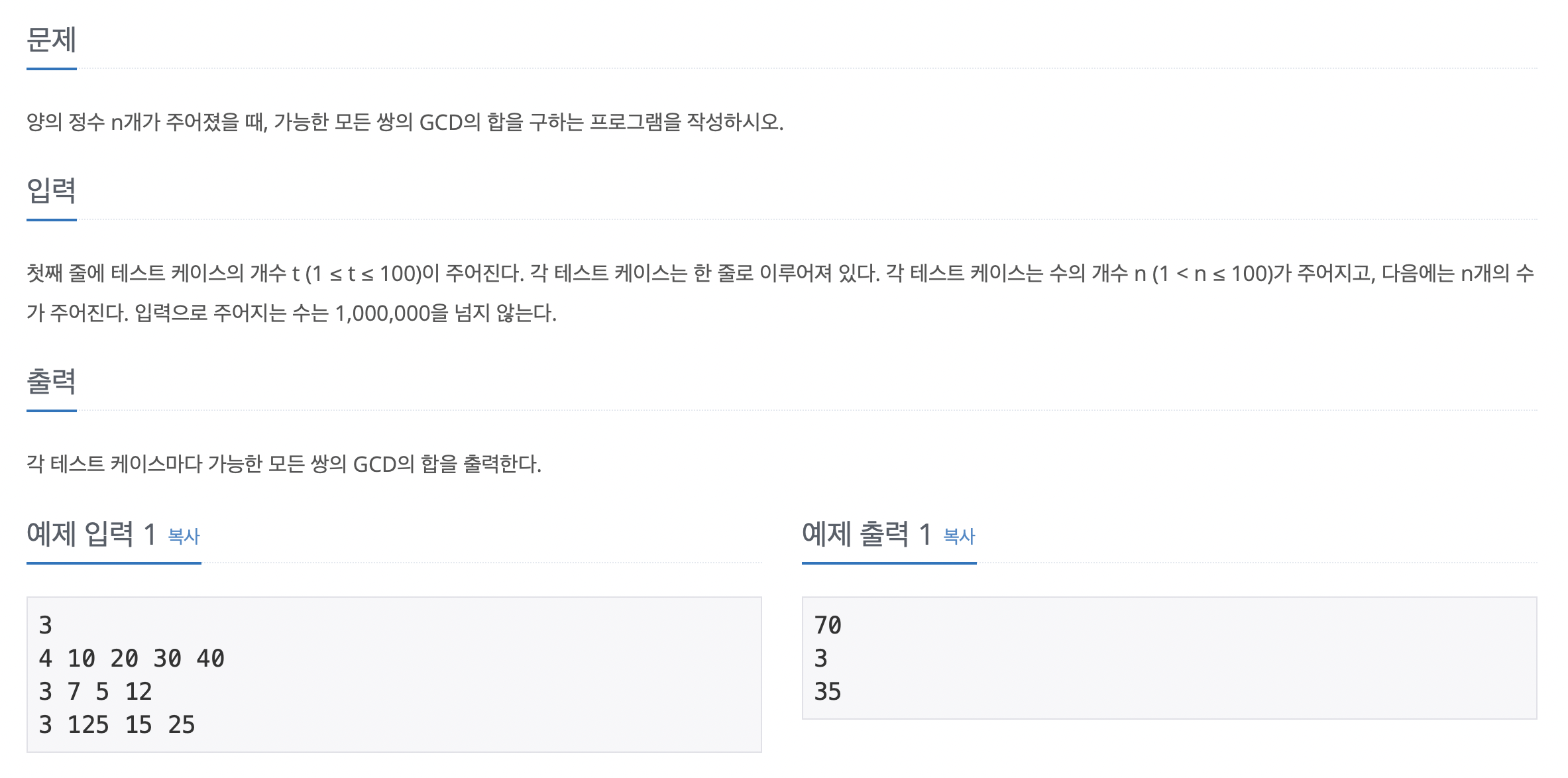
유클리드 호제법을 활용하여 두 수의 최대공약수를 구할 수 있으며, 이 최대공약수를
각 경우마다 모두더하여 최종 값을 출력
👀 참고: 유클리드 호제법
a, b 두 수가 있을 경우 a를 b로 나눈 나머지를 이용하여 최대 공약수를 구하는 오래된 알고리즘
a % b의 결과가 다음 계산의 b가 되며, b가 다음 계산의 a가 된다
이때 b가 0이 될 때까지 계산을 반복하며 그때의 a가 최대 공약수가 된다
(왜 그렇게 되는지는 유클리드 호제법을 찾아보시길..)
🌱 코드 in Python
알고리즘: Brute Force
import sys, math
t = int(sys.stdin.readline())
def get_gcd(a, b): # while문을 활용한 유클리드 호제법 구현
while b :
a, b = b, a % b
return a
for i in range(t):
case = list(map(int, sys.stdin.readline().split()))
n = case[0]
sum = 0
for j in range(1, n): # 숫자 개수를 제외한 첫번째 인덱스부터 마지막 인덱스 직전까지 순회 (2개의 수를 계산해야 하므로)
for k in range(j + 1, n + 1): # 앞 항의 다음 항부터 끝까지 순회하며 전체 케이스 탐색
sum += get_gcd(case[j], case[k])
print(sum)각 케이스 별 모든 최대공약수의 합을 구해야 하므로 전체적으로 탐색하는 브루트포스 알고리즘을 활용하여 문제를 풀었다
해당 코드에서 GCD를 구할 때에는 while문을 활용하여 유클리드 호제법을 구현하였으나, 이 외에도 여러 방법이 있다
def get_gcd(a, b):
if b == 0:
return a
return get_gcd(b, a % b)먼저 재귀문을 활용한 gcd 계산 방법이다
로직 자체는 while문을 활용했을때와 같다 다만 어떻게 표현 하느냐 정도의 차이..
시간 복잡도에서도 결국 b가 될 때까지 반복하는 거니까 별로 차이가 없지 않을까? (잘모름)
import math
for i in range(t):
case = list(map(int, sys.stdin.readline().split()))
n = case[0]
sum = 0
for j in range(1, n):
for k in range(j + 1, n + 1):
sum += math.gcd(case[j], case[k]) # math 모듈 내 gcd 함수 활용
print(sum)다음은 math 모듈 중 gcd 함수를 활용한 방법이다
다만 어디서 보기로 실제 구현한 것이나 gcd함수를 활용하는 것이나 시간 차이가 별로 없다고 한다
방법은 많이 알아두면 알아둘수록 좋으니까!
🧠 기억하자
문제에서 전체적으로, 모든 경우의 수 이런 느낌이 나오면 대부분 bruteforce 알고리즘으로 풀어야 하는 것 같다
아직 공부를 많이 안해서 사실 그리디나 브루트포스나 뭐가 다른지 잘 모르겠음! 그리디는 대충 이름만 알고있기는 함 헤헤
지금까지는 그냥 첨부터 무식하게 다 해본다! 이걸 알고리즘이란 이름으로 참 유식하게 포장했구나! 하는 마음
아무튼, 이런 경우에는 일단 for문을 어디서부터 어디까지 돌려서 최적의 해를 구하느냐가 관건인 거 같다
그리고 파이썬은 정말 없는 게 없다. 오늘 배운 것은 gcd함수!
이 문제는 gcd 구하는 방법을 몰라서 그 부분이 조금 어려웠을 뿐 크게 어려운 부분은 없었다!
1일 1알고리즘 가보자고!

