[Algorithm] Dynamic Programming / 동적 계획법

최율·2022년 11월 23일

Algorithm

목록 보기

5/5

🧗‍♀️ Dynamic Programming 이란?

인간이 문제를 풀어내는 방법을 생각해보자.

문제가 주어진다.
1. 풀 수 있는 경우 → 풀면 된다!
2. 풀 수 없는 경우
  1. 그냥 못 풀겠다… → 답이 없음
  2. 문제의 스케일이 작아지면 풀 수 있을 것 같다!

그렇다면 우리가 ‘문제의 스케일이 작은 경우에만 풀 수 있는 경우’를 예시와 함께 알아보자.

하노이 탑 문제

~~동적 계획법 설명에 있어 크게 중요하지 않은 문제니 전체적인 흐름만 확인하시고 생략해도 좋습니다.~~

위 3개의 기둥 중 왼쪽에 쌓인 원반을 오른쪽 기둥으로 모두 옮기는 문제이며 조건은 다음과 같다.

더 큰 원반이 그보다 더 작은 원반 위에 존재해서는 안된다. 이는 옮기는 과정에서도 동일하게 적용된다.
원반은 한 번에 하나씩만 옮길 수 있다.

원반이 총 n개 쌓여 있을 때, 모두 오른쪽 기둥으로 옮기는 경우 원반은 총 몇 번 옮겨지는가?

```
만약 원반이 1개 있다면? 
```
원반을 그냥 한 번 옮기면 된다.
```
만약 원반이 2개라면? 
```
첫 번째 원반을 가운데에 옮긴 뒤 두 번째 원반을 오른쪽 기둥에 넣고 첫 번째 원반을 위에 얹으면 된다.
```
만약 원반이 3개라면?
```
이 때부터 조금씩 복잡해진다.

💡아이디어

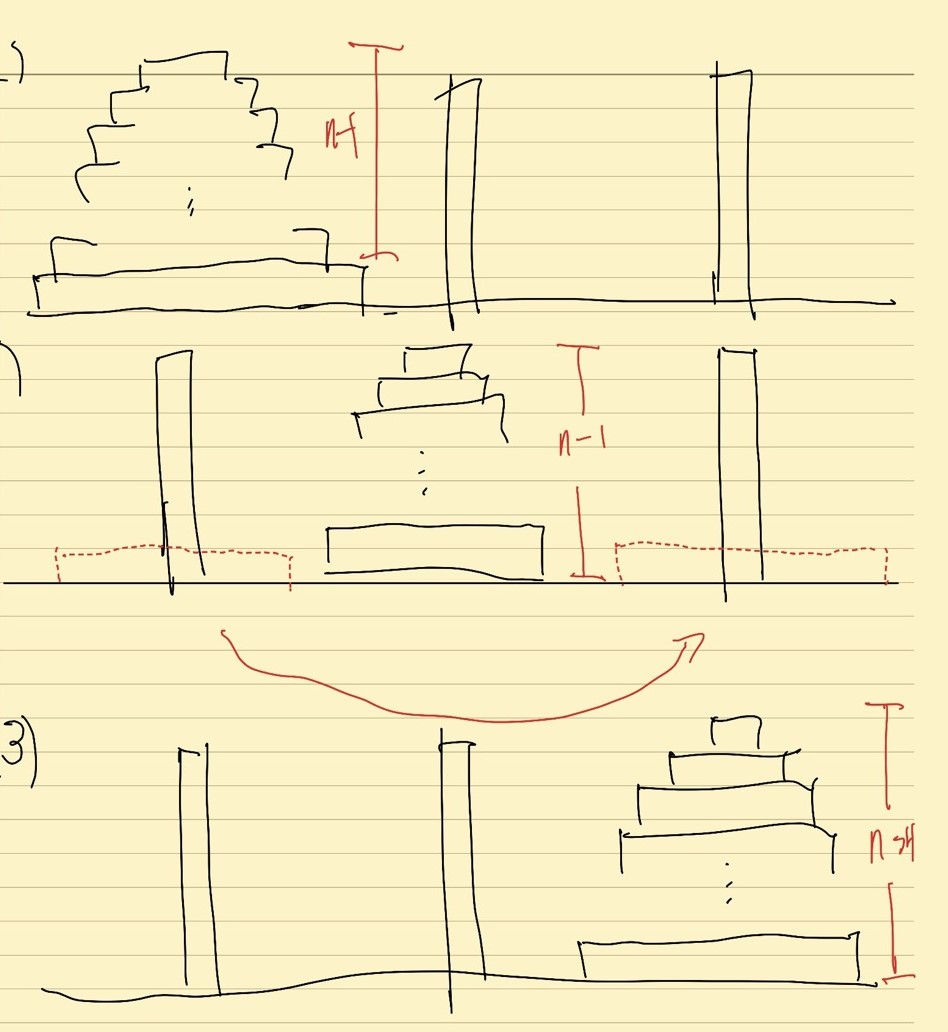
n개의 원반을 옮길 때, 필연적으로 마지막 n번째 원반을 3번째 기둥에 위치한 뒤, 나머지 n-1개의 원반을 옮겨야 한다.
그 점을 이용하여 n개의 원반을 옮기는 데 필요한 옮김 횟수를 $F(n)$ 이라 하면
$F(n) = F(n-1) + 1 + F(n-1)$ 이라는 식을 얻을 수 있다.
a. 이를 더 나열해 보면.. $F(n) = 2F(n-1) + 1$
b. $F(n) = 2(2F(n-2) + 1) + 1$
c. $F(n) = 2(2(2F(n-3) + 1) +1) + 1$ .
d. 이를 일반화 하면 $F(n) = 2^kF(n-k) + (2^{k-1} + 2^{k-2} +...+ 1)$
e. $F(n) = 2^n -1$ ( $when \space k = n-1$ )

여기서 중요한 것은 실제 횟수를 구하는것이 중요한 게 아닌!
우리가 풀 수 있는 영역과 감이 잘 오지 않는 영역을 구분하여 결합하는 것이다.

위 문제에서 우리가 풀 수 있는 영역은 원반이 3개 정도일 때고, 그 이상은 구하기 쉽지 않다.

따라서 문제의 크기를 n부터 우리가 잘 아는 1,2,3 개 정도일 때로 축소하는 것이다.

뭐야?! 문제를 재귀로 푸는게 다인데? 동적 계획법이 뭐가 특별하다는 거죠?

→ 동적 계획법은 재귀로 풀어야 하는 문제의 규모가 커질 때 특별해진다.

동적 계획법이 무엇인지, 재귀와 다른것은 무엇인지, 어느때 효과가 있는지 예제와 함께 알아보자.

피보나치 수열

피보나치 수열이 무엇인지는 해당 링크에서 개요를 참조!

피보나치 수열을 구하는 코드는 다음과 같다. (재귀를 사용)

def fibo(n):
	if n == 0 or n == 1: return n
	else: return fibo(n-1) + fibo(n-2)

간단한 재귀 함수 코드이다. 그런데 위 코드는 문제가 있다.

바로 쓸데없는 연산을 너무 많이 한다는 것.

5번째 피보나치 수를 구하는 경우를 생각해보자

$f(5) = f(4) + f(3) = (f(3) + f(2)) + f(3)$ → 이 과정에서 3번째 피보나치 수를 두 번 구하게 된다.

혹시 “에이~ 한 번 정도 더 연산하는건데 뭐 어때요~” 라고 생각했다면 다음과 같은 경우를 생각해보자.

100부터 500까지의 피보나치 수열을 구해야한다면?
1. 100번째 피보나치 수열을 구하고, 101번째 피보나치 수열을 구할 때 또 다시 1부터 더해나가야 한다.
재귀 함수의 코드상 스택 메모리에 함수 반환 주소가 저장되는데, 스택 메모리가 부족하다면?

동적 계획법의 등장

피보나치 수열을 구할 때 마다 따로 저장해두자!

…

이게 전부다.

그렇다면 피보나치 수열에 동적 계획법을 적용하여 코드를 작성해보자!

def fibo(F:list, n):
	if F[n] > 0:
		return F[n]
	else:
		F[n] = fibo(F, n-1) + fibo(F, n-2)
		return F[n]

fibo_list = [0 for _ in range(1000)]
fibo_list[0] = 1
fibo_list[1] = 1